现代密码学中的数论基础知识梳理

 

 导读

数论是一门研究自然数之间的关系和规律的学科，普遍认为是纯数学的分支，但并非是完全没有实用性的学科。现代密码学中用到了很多基础数论中的结论，特别是公钥加密体系（例如RSA算法，椭圆曲线加密等）。

本文目的在于梳理现代密码学中常用到的基础数论方面的定理和结论。其中包括素数的特性、欧几里德算法、线性方程定理、算术基本定理、模算数运算、线性同余定理、欧拉函数、费马小定理、中国剩余定理、欧拉定理、本原根、离散对数问题等等一些基础知识。了解这些知识，应该能够理解现代密码学中经典的

Diffie-Hellman密钥协商和RSA算法的原理，进而能够理解秘钥管理、数字签名、消息认证、公钥证书等密码学领域的问题。

本文很大程度上参考了数论概述里面的内容，也借鉴了算法导论和密码编码学与网络安全原理与实践的相关章节。

一、关于互质和整除的一些有用结论和定理

数论对素数的特性尤其感兴趣，素数是整数的基础构件，就像是元素在化学式中的作用类似。

1、d整除a记作：d∣a
如果d∣a且d∣b，那么d∣(ax+by).

2、如果p是素数，且p整除乘积ab，则p整除a或者p整除b（或者p同时整除a和b）。

证明的关键是假设p不整除a，考虑1=gcd(p,a)同时整除p和a。但由于p是素数，p的因子只能是1或者p，所以gcd(p,a)=1。由后面的线性方程定理得知，可以构造线性方程px+ay=1=gcd(p,a)，两边同时乘上b，得bpx+aby=b，p整除左边等价于p整除右边的b。p不整除b的情况可以用同样的方式证明。

拓展：如果素数p整除整数乘积a1a2a3...ar,则p至少整除a1,a2,a2,...,ar中至少一个因数。

3、1和任意一个自然数是都是互质关系。

4、任意两个质数构成互质关系。

5、一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10。

6、如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57。

7、 p是大于1的整数，则p和p−1构成互质关系，比如57和56。

8、p是大于1的奇数，则p和p−2构成互质关系，比如17和15。

9、素数p与1到p−1的任意整数均互质。并且阶乘(p−1)!与p互质，这个结论在后面费马小定理和欧拉定理的证明过程中会用到。

二、欧几里德算法

欧几里德算法的原理和流程其实比较容易理解。

(GCD递归定理) ：对于任意的非负整数a和正整数b，满足

gcd(a,b)=gcd(b,amodb)
更详细的将，其计算流程：

a=q1×b+r1b=q2×r1+r2r1=q3×r2+r3r2=q4×r3+r4...rn−3=qn−1×rn−2+rn−1rn−2=qn×rn−1+rnrn−1=qn+1×rn+0
rn即为求得的a和b的最大公约数。

以上流程主要需要思考三个问题：

1）为什么rn是公约数？（需要从下往上推理）

2）为什么rn是最大的公约数？（假设d是a与b的任意公约数，如果能够证明d整数rn，即可得证。）

3）为什么欧几里德算法最后一定会终止？（因为每轮辗转之后的余数是单调递减的，辗转的轮次数有上界，最后一定能够保证余数为0，然后取最后一个非零余数rn就是正确的结果。）

算法实现Demo：

复制代码
//欧几里德算法迭代实现
public static int getGCD(int a,int b) {
if (a<b) {//保证a>=b
return getGCD(b, a);
}
if (b>=1) {//保证b>=1
int temp = 0;
while(b>0) {
temp = a%b;
a = b;
b = temp;
}
return a;
}else {
return -1;
}
}
复制代码

三、扩展欧几里德算法

扩展欧几里德算法可以用来求解一类有意思的线性方程的整数解，该线性方程的整数求解过程与最大公约数有密切关系。

对于线性方程（a,b,c为常数）：

ax+by=c
是很熟悉的方程。这里讨论情况是a,b,c满足一定的关系：c=gcd(a,b)，也即是这样的线性方程：

ax+by=gcd(a,b)
这个线性方程必然有整数解，但我们更关心如果用更好算法去求解，该算法利用欧几里德算法求解最大公约数过程中的中间商和余数，进行扩展运算，在求gcd(a,b)的过程中，同时也就求得线性方程的整数解(x,y)。

算法实现Demo：

复制代码
public static long[] gcdExt(long a,long b){
long ans;
long[] result=new long[3];
if(b==0)
{
result[0]=a;
result[1]=1;
result[2]=0;
return result;
}
long [] temp=gcdExt(b,a%b);
ans = temp[0];
result[0]=ans;
result[1]=temp[2];
result[2]=temp[1]-(a/b)*temp[2];
return result;
}
复制代码

四、算术基本定理

(算术基本定理)：每个整数n⩾2可唯一分解成素数的乘积：

n=pe11pe22...perr
其中，pi为素数，且p1<p2<...<pr，ei为正整数。

实际上，看似理所当然的事实，其实并非如此。如果自定义一个有别正整数集合的其他集合，很可能就不再满足唯一分解定理。例如，集合E是由偶数构成的集合：

E={0,2,4,6,8,10,12...}
也可在这个集合中定义所谓的“素数”，称之为“E-素数”，2,6,10,14,18,22,26,30都是“E-素数”。对这个集合中的元素尝试做“素因子”分解，并不总是能都到唯一分解的结果，例如180=10x18=2x30，存在两种“E-素数”的分解形式。

实际上算术基本定理包含两个方面：

1）n可以分解成素数乘积的形式。

2）仅有一种这样的素因子分解的形式（当然这里不考虑因数重排序的情况）。

显然唯一性分解是算术基本定理的关键和重点。

另外一个有意思的事实：

如果n是一个合数，则在小于等于n−−√的数中必定有一个数a整除合数n。

该结论基于算术基本定理：合数n必定可以唯一分解多个素数的乘积，这里假设p是它的素因子中最小的一个，则n必定可以写成n=p×m的形式，这里的m是其余大于等于p的素因子的乘积，显然m⩾p,因此n=p×m⩾p×p=p2
所以，在0...n−−√的范围内，必定存在一个数a整除n。

可以利用这种方法简单的分辨一个数是否是素数，也可以反复执行上述过程将一个较小的合数进行素因子分解。

五、 同余式与模算术

一般来讲，可以将mod视为一种求余数的二元运算符，例如2=5mod3；也可以用来表示同余关系，这种同余关系通常用同余式表示。例如2≡5(mod3)表示模3时2与5同余。

同余式虽然有别于普通的算数运算下的等式，但是具有相同模的同余式与普通等式有一些相似的特性：

如果已知：

a1≡b1(modm) 且a2≡b2(modm)
那么有：

a2±a2≡b2±b2(modm)和a2a2≡b2b2(modm)
同时，也不难得出：

如果，ak≡b(modm)，那么，(ak)j≡bj(modm)
特别的当b=1时：

如果ak≡1(modm)，那么，(ak)j≡1(modm)。

但是，由ac≡bc(modm)不一定能得到a≡b(modm)。

例如2×25≡2×20(mod10)，但是25≢20(mod10)。

只有当c和m互质时（也即是gcd=(c,m)=1），才能够从同余式两边消去c。

由同余式可以引出同余方程：

ax≡c(modm)
求解上述同余方程有一个定理，叫做同余方程定理。

(同余方程定理)：设a,c,m是整数，m⩾1，且设g=gcd(a,m)，则

1）如果g不整除c，那么同余方程ax≡c(modm)没有解。

2）如果g整除c，那么同余方程ax≡c(modm)恰好有g个解。

以上同余方程的求解过程需要用到扩展欧几里德的求解方法。实际上ax≡c(modm)可以转化为线性方程ax+m(−y)=c。

特别地，当a和m互质，即g=gcd(a,m)=1时，同余方程变成：

ax≡1(modm)
a和x互为模反元素，这在RSA公钥加密算法生成秘钥过程中有应用。

六、费马小定理

费马小定理揭示了整数的幂在模运算下的特殊规律。

(费马小定理)：设p是素数，a是任意的正整数且满足a≢0(modp)，则

ap−1≡1(modp)
实际上对于条件的更简单的表述可以为"a与素数p互质"即可。

证明费马小定理并不是非常难，证明过程是基于这样一个结论：

设素数p与任意正整数a互质，那么集合S={a,2a,3a,...(p−1)a}中任意任意两个元素均不可能模p同余。也即是ja≢ka(modp)。其证明过程只需要利用反证法即可。

上述结论表明，如果对集合S中的每一个元素模p的结果，其结果刚好与集合T={1,2,3,4...(p−1)}中的元素一一对应（不考虑次序重排）。

于是有：

a×2a×3a...×(p−1)a≡1×2×3...×(p−1)(modp)
稍微整理得：

(p−1)!×ap−1≡(p−1)!(modp)
这里必然后gcd((p−1)!,p)=1，所以，可以两边消去(p−1)!，得到ap−1≡1(modp)。

正是由于存在这样的关系，所有费马小定理可以用来简化对整数的幂取模的计算。

费马小定理在数论中非常重要，与其三个定理（分别是威尔逊定理、欧拉定理和中国剩余定理）合称数论四大基本定理。更有趣的是，费马小定理实际上可以视为欧拉定理的一个特例。

最后，费马小定理还有一种等价的表示形式：

若p是素数，a是正整数，则

ap−1≡a(modp)
这里不需要a与p互质的条件。这并不是一件很奇怪的事情，无非是利用模算术的除法特性（见同余式与模算术）的变形。

七、中国剩余定理

中国剩余定理（也叫作孙子定理）所描述的问题在小学课本中都能找到，只不过当时只能用方程组去刻画这个的问题。

在数论中，它有不止一种表述形式，我见到的就至少有两种。

其中一种比较易懂的描述为：

设m,n是正整数，gcd(m,n)=1，b,c是任意正整数，则同余方程组

x≡b(modm)x≡c(modn)
恰有一个解0⩽x⩽mn。

以上是从方程的角度描述，另外一种从对应的角度(数与k元组的对应关系)表述也是可行的，可以看做是上面表述形式更抽象的扩展：

令

M=∏ki=1mi，其中mi两两互质

则ZM={0,1,2,3...(m−1)}中任意整数会对应一个k元组：

A↔(a1,a2...,ak)
其中ai当然是要在Zmi中(也即是ai∈Zmi)，并且ai由关系ai=Amodmi给出。

从以上定理实际上可以推断出A与k元组唯一一对应的事实。

以上描述形式是算法导论和密码编码学与网络安全--原理与实践中采用的表述形式。相比于第一种表述形式，第二种表述更具有通用性，也更抽象。中国剩余在推导欧拉函数求解公式时会用到。

八、欧拉函数

欧拉函数ϕ(m)的含义是1到m−1中（也就是[1,m−1]）且与m互质的整数的个数。它是数论中一个非常重要的函数。

如何计算欧拉函数的值是一个关键的问题。欧拉函数的计算方法的推导主要用到两个结论：

（1）如果p是素数，k⩾1，则ϕ(pk)=pk−pk−1=pk(1−1p)
（2）如果gcd(m,n)=1，则ϕ(mn)=ϕ(m)×ϕ(n)
证明（1）的思路很简单：从1到pk共有pk个整数，这些整数中当然有可能存在与pk不互质的数，那么只要扣除去这些数就可以了。显而易见的是，这些与pk不互质的数并不难找，它们分别是：

p,2p,3p,...,(pk−1−2)×p,(pk−1−1)×p,pk−1×p
一共有pk−1个数与pk不互质，那么从pk中扣除这pk−1个数即可。

证明（2）比较复杂一点，其思路是采用计数的思想然后结合中国剩余定理（第一种表述形式）来证明。

有了以上两个结论，结合算术基本定理，可以得到计算ϕ(m)比较通用的公式：

假设任意正整数m，且其素因子分解形式为

m=pk11pk22...pkrr
利用上面的（2）可以得到

ϕ(m)=ϕ(pk11)ϕ(pk22)...ϕ(pkrr)
然后利用（1），继续得到

ϕ(m)=pk11pk22...pkrr(1−1p1)(1−1p2)...(1−1pr)
也就是

ϕ(m)=m(1−1p1)(1−1p2)...(1−1pr)
例如

ϕ(12)=ϕ(22×3)=ϕ(22)×ϕ(3)=12×(1−12)×(1−13)=4
另外，欧拉函数与各因数之间存在一种巧妙的关系：

设d1,d2,...,dr是n的因数，则

ϕ(d1)+ϕ(d2)+...+ϕ(dr)=ϕ(n)
其实当n=p或者n=p2甚至n=pk（p是素数）时，很容易验证其正确性。

九、欧拉定理

欧拉定理与费马小定理同样都是揭示了整数的幂在模运算下的特殊规律，实际上他们有微妙的关系。

(欧拉定理)：如果gcd(a,m)=1，则

aϕ(m)≡1(modm)
实际上证明欧拉定理的方法与证明费马小定理基本类似，此处略去。

欧拉定理与费马小定理有微妙的关系：如果这里的m是一个素数，则ϕ(m)=m−1，由此得到费马小定理。说明费马小定理实际上可以看成欧拉定理的一个特例。

与费马小定理类似，欧拉定理也有另外一种表现形式：

aϕ(m)+1≡a(modm)
这里没有要求a与m互质的条件。

十、模反元素

如果两个正整数a和m互质，那么一定可以找到整数b，使得 ab−1 被m整除，或者说ab被m除的余数是1。

ab≡1(modm)
则此时b就是a的模反元素。

实际上这里相当于求解同余方程ax≡1(modm)，当gcd(a,m)=1时，必定存在一个整数解，因此模反元素必定存在，此解即是a的模反元素。

从欧拉定理的角度

aϕ(m)=a×aϕ(m)−1≡1(modm)
也可以证明模反元素是存在的。

更进一步，如果p是素数，由集合Zp={0,1,2,...p−1}和二元运算模p的算术运算构成一个有限交换群G。G中每一个元素都有乘法逆元，此乘法逆元就是这里的模反元素。

十一、本原根

本原根通常与幂模有关，观察如下例子：

 

 

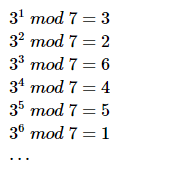
 可以发现3的各幂次模n能够得到一个循环的序列{3,2,6,4,5,1}，这个序列刚好对应着小于等于7且与7互质的整数集合。

这并非一个偶然规律，2或者3的各次幂模5，2或者6或者7或者8的各次幂模11都能够得到同样的规律。

当然也并不是总是这样，例如

 

 

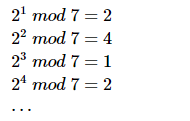
 更一般的，考虑p为素数，gcd(a,p)=1且a⩽p−1，如下序列

 

 

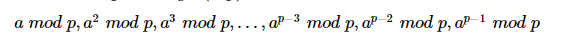
 如果

 

 

 

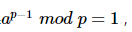
，那么可以证明上述序列值必然各不相同（证明可以用反证法，不存在ai≡aj(modp)的情况）。因为这里模p运算的结果总会映射到集合Zp={1,2,3,...,p−2,p−1}，这个集合中的每个元素与p互质。也即是说不考虑次序重排，上述序列值对应了集合Zp的值。

这时称a是p的本原根或者生成元。

并非所有的整数都存在本原根，事实上只有

 

 

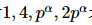
 才有本原根，其中p是任意奇素数，可见素数一定存在本原根。

(原根定理)：每个素数p都有本原根，而且刚好有ϕ(p−1)个模p的本原根。（ϕ指的是欧拉函数）

另外还有一些值得挖掘的规律，不难发现，对于

 

 

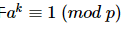
 ，这样的k可能不止一个，比如：

 

 

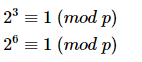
取最小的k称为a模p的阶：

 

 

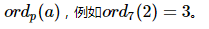
 不难发现，

 

 

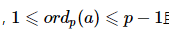
 且总是整除p−1（从费马小定理的角度思考可以容易得出结论）。

十二、离散对数问题

离散对数的问题很好理解，与算术对数相对，只是在算术对数的基础上增加了模运算。

对于

 

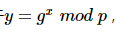
 ，如果已知x,g,p求y是比较容易的求解的；但是反过来，已知y,g,p求x是很困难的，因此这里可以看成一个单向函数。

Diffie-Hellman密钥协商原理正是基于这样的离散对数问题而设计。而椭圆曲线加密是基于定义在椭圆曲线上的特殊加法运算规则下的离散对数问题而设计，两者达到的目的是一致的，都是利用某一个方向上的计算困难程度保证加密算法的机密性。

十三、References

1、数论概述

2、算法导论.第三一章.数论算法

3、密码编码学与网络安全原理与实践

 

 

https://www.cnblogs.com/qcblog/p/8976017.html