VINS中的边缘化
VINS中的边缘化
1. 边缘化回顾
1.1 感性回顾-无公式
\(\quad\)首先来看一些VINS中维护的状态变量:是由para_Pose(6维,相机位姿); para_SpeedBias(9维,相机速度、加速度偏置、角速度偏置)、para_Ex_Pose(6维,相机IMU外参)、para_Feature(1维,特征点深度)、para_Td(1维,标定同步时间)共5部分组成,在后面进行边缘化操作时这些优化变量都是当做整体去处理。
\(\quad\)我们在前面已经介绍了滑动窗口算法,滑动窗口算法其实就是用来进行边缘化的,只不过上一篇文章我们介绍的是纯理论工作,这里我们从直观上以及程序中来对边缘化或者说滑动窗口算法进行理解。VINS中的边缘化的是滑动窗口中的最老帧或者次新帧,将滑窗内的某些较旧或者不满足要求的视觉帧剔除,所以边缘化也被描述为将联合概率分布分解为边缘概率分布和条件概率分布的过程(就是利用 Schur 补减少优化参数的过程)。
\(\quad\)对于滑窗外的状态,我们不去进行优化,但也不能直接丢掉,这样会破坏原有的约束关系,损失约束信息。采用边缘化的技巧,将约束信息转化为待优化变量的先验分布,实际上是一个从联合分布中获得变量子集概率分布的问题。
\(\quad\)执行边缘化过程中,我们需要不断迭代计算H矩阵和残差b,而迭代过程中,状态变量会被不断更新,计算边缘化相关的雅克比时需要注意固定线性化点。也就是计算雅克比时求导变量的值要固定,而不是用每次迭代更新以后的x去求雅克比,这就是FEJ(First Estimate Jacobians)。也被称为系统的一致性问题。
- 为什么需要边缘化?
\(\quad\)随着系统的不断运行,观测和残差以及待优化的状态变量会不断增加,这会使得优化问题逐渐变得庞大,系统无法进行实时求解,此时我们就想着能不能从系统中删除掉某些观测和状态变量,至于怎么删除,删除哪个在VIO系统中是有讲究的,一般是通过概率论的角度,或者具体点说通过联合概率分布和条件概率分布的相关理论来进行分析和研究。
\(\quad\)边缘化目标是不再计算这一帧的位姿,甚至可能会不计算该帧相关的一些路标点,但希望保留该帧对滑动窗口内其他帧的约束关系,这样不会减少约束信息,利于对状态变量优化,在移出位姿或特征的时候,需要将相关联的约束转变成一个约束项作为先验放到优化问题中,这就是marginalization要做的事情。否则,将 pose 移出窗口时,丢掉与其相关的所有约束,会导致求解精度下降,且当机器人进行退化运动(如: 匀速运动)时,没有历史信息做约束的话是无法求解的。
VINS 中的边缘化与 G2O 计算过程中的边缘化意义不大相同(虽然处理方法一致): G2O 中对路标点设置边缘化(pPoint->setMarginalized(true))是为了在计算求解过程中,先消去路标点变量,实现先求解相机位姿,然后再利用求解出来的相机位姿反过来计算路标点的过程,目的是为了加速求解,并非真的将路标点给边缘化掉;而VINS 中则真正需要边缘化掉滑动窗口中的最老帧或者次新帧,目的是希望不再计算这一帧的位姿或者与其相关的路标点,但是希望保留该帧对窗口内其他帧的约束关系。
简单来说,舒尔补不但可以用来进行边缘化,还能加速矩阵的求解。
1.2 一个边缘化的例子
\(\quad\)下面我们用一个具体例子来形象说明边缘化过程及其导致的矩阵稠密现象(fill-in)。假设有四个相机位姿\(x_{pi}\),以及 6 个路标点\(x_{mk}\),(路标点用 xyz 的参数化), 相机与路标点的边表示一次观测,相邻相机之间的边表示 IMU 约束,4个相机观测到6个路标点,同时带有IMU约束的相互关系如下:
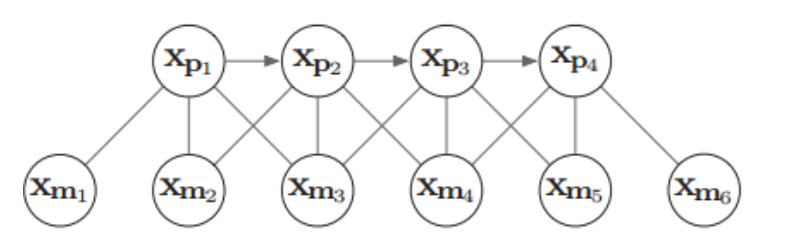
下面尝试给\(x_{p1}\)给marg掉,然后将\(x_{m1}\)给marg掉,看看\(H\)矩阵会如何变化。变化过程如下图所示:
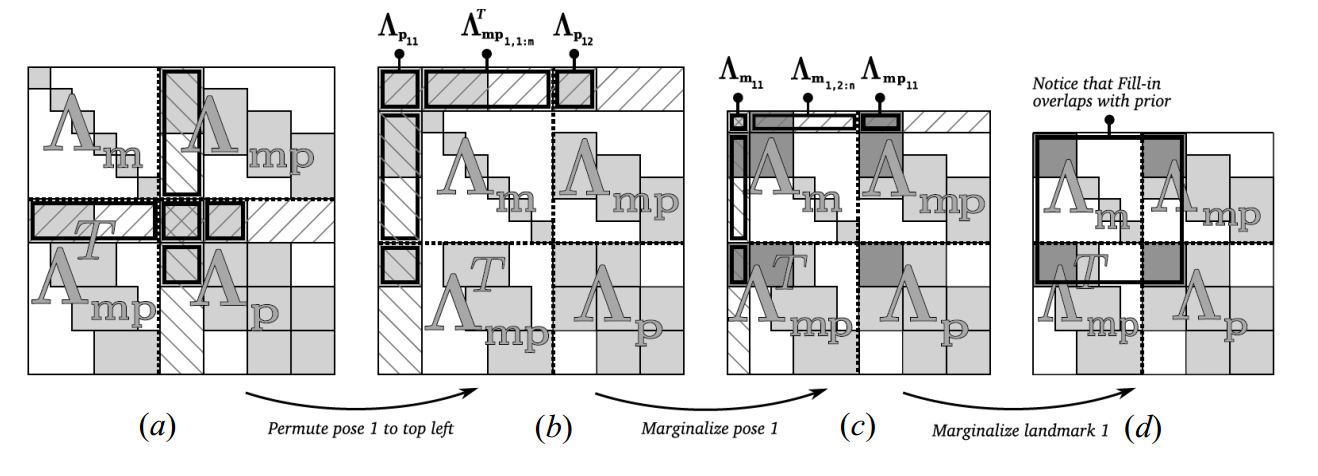
下面我们对上图进行详细说明, 下图表示原始的 H 矩阵,注意这里的左上角为路标点相关部分,而右下角是 pose 相关部分。
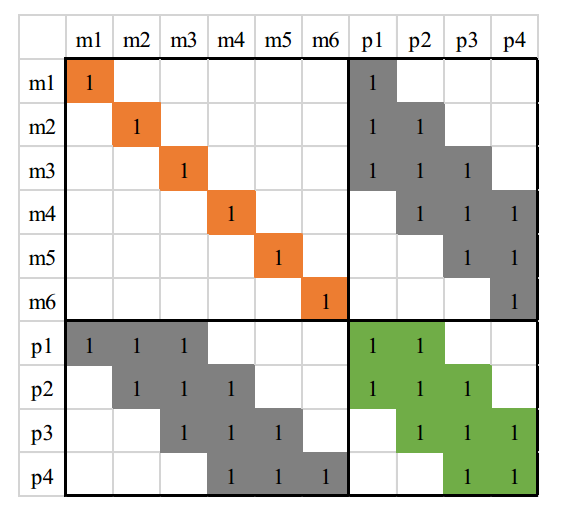
接下来是把 H 矩阵中跟\(x_{p1}\)相关的部分移动到 \(H\) 矩阵左上角。
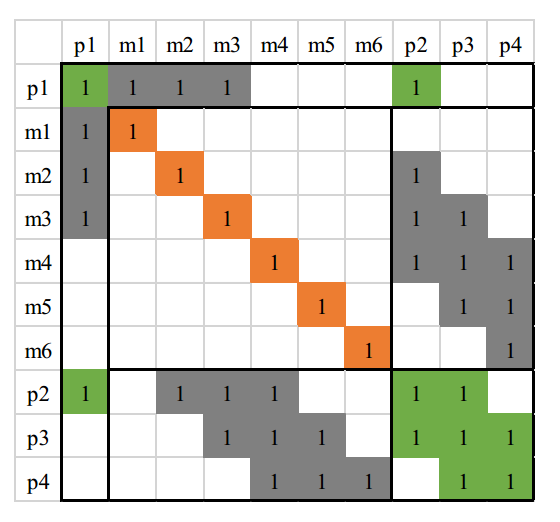
下图是把\(x_{p1}\)边缘掉后的 H 矩阵,这里矩阵的大小为 36x36。我们可以看到相对于原始的H矩阵,其变得更加稠密了,也就是说Marg掉一个pose会使得剩余的H矩阵有三个地方被fill-in,如下图中颜色加重的区域(黄色区域)。
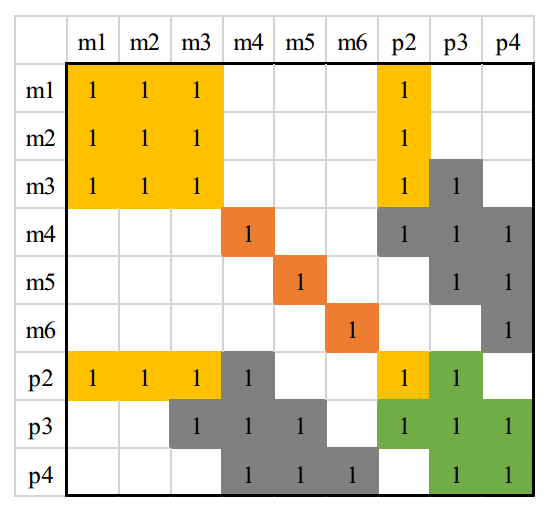
这时图关系则变成了:
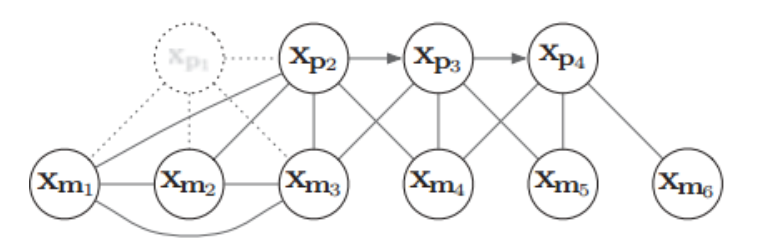
注意, 观察上图可发现这时的\(x_{m1},x_{m2}\)和\(x_{m3}\)彼此之间已经产生了新的约束关系,且\(x_{p2},x_{m1}\)产生了新的约束关系。
下图是marg掉 \(x_{m1}\)后的\(H\)矩阵。
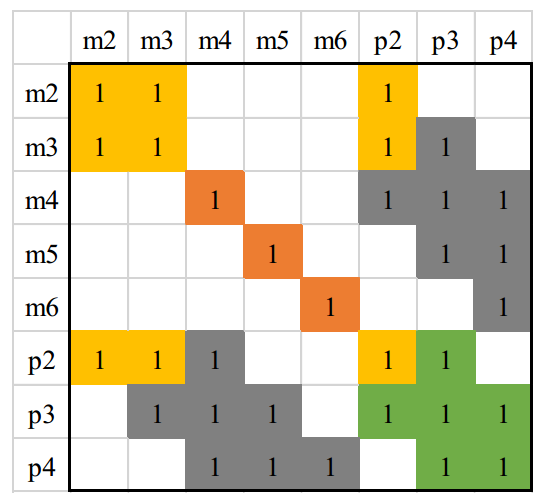
对应的图关系如下:
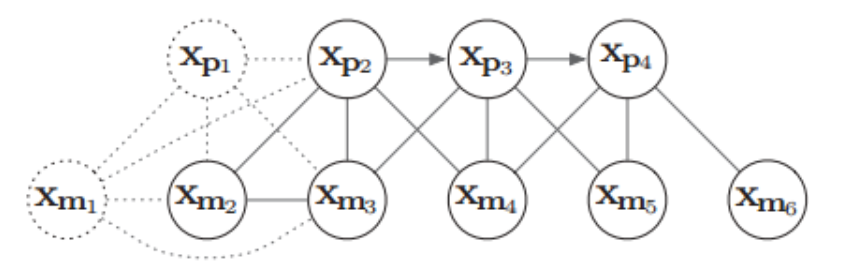
我们发现, marg 掉\(x_{m1}\)后,并没有是 H 矩阵更稠密,这是因为\(x_{m1}\)之前并未与其他pose 有约束关系,即并未被观察到,因此如果 marg 掉那些不被其他帧观测到的路标点,不会显著地使 H 矩阵变得稠密。 而要 marg 掉的路标点中, 对于那些被其他帧观测到路标点,要么就别设置为 marg,要么就宁愿丢弃,这就是 OKVIS 中用到的策略。
1.3 VINS中的两种边缘化策略
\(\quad\)MARGIN_NEW,保证保留那些视差比较大的pose,如果这种情况一直MARGIN_OLD,导致视觉约束不够强,状态估计会受IMU积分误差影响较大。在MARGIN_OLD中,滑窗中第1帧Pose状态量的边缘化会使H矩阵更稠密,另外MARGIN_OLD中第1帧对应的路标点也要边缘化掉,如果这些路标点与其他帧Pose状态量无关,则其不会使H矩阵变稠密,如果有关,则会使得H矩阵变得更稠密,显然当前策略会影响计算速度。
-
MARGIN_OLD:如果次新帧是关键帧,则丢弃滑动窗口内最老的图像帧,同时对与该图像帧关联的约束项进行边缘化处理。这里需注意,如果该关键帧是观察到某个地图点的第一帧,则需要把该地图点的深度转移到后面的图像帧中去。
-
MARGIN_NEW:如果次新帧不是关键帧,则丢弃当前帧的前一帧。因为判定当前帧不是关键帧的条件就是当前帧与前一帧视差很小,也就是说当前帧和前一帧很相似,这种情况下直接丢弃前一帧,然后用当前帧代替前一帧。为什么这里可以不对前一帧进行边缘化,而是直接丢弃,原因就是当前帧和前一帧很相似,因此当前帧与地图点之间的约束和前一帧与地图点之间的约束是很接近的,直接丢弃并不会造成整个约束关系丢失信息。这里需注意,要把当前帧和前一帧之间的 IMU 预积分转换为当前帧和前二帧之间的 IMU 预积分。
2. VINS-Fusion中边缘化代码分析
\(\quad\)VINS 中并未使用 FEJ 的策略, 这里我们进行简要说明: 对于滑窗内剩余的优化变量, 如倒数第二帧位姿 T1,当边缘化掉最老帧 T0 后,会给 T1 加上新的约束。值得注意的是, 这个新约束的线性化点是在 marg 掉 T0 时刻的 T1 的值,而当之后 T1 迭代更新后,该marg 产生的约束并不会调整线性化点,即不会在新的 T1 处重新展开,这样会导致两次的线性化点不一致。但据作者描述因未发现明显的 yaw 不可观性变化导致的轨迹漂移, 因此并未采用 FEJ 策略,反而加入 FEJ 后导致结果不佳。
首先VINS进行边缘化之前会有个条件判断,如果滑窗内的帧还没满也就没必要进行边缘化。
if(frame_count < WINDOW_SIZE)
return;
接下来我们要先来分析一下边缘化操作涉及到的几个类
-
ResidualBlockInfo -
MarginalizationInfo -
MarginalizationFactor
这三个类的关系以及流程大概是这样的:
- 首先创建一个 MarginalizationInfo 的指针。
- 然后不断地向里面添加 ResidualBlockInfo,ResidualBlockInfo和每个具体的残差关联起来,包括MarginalizationFactor, IMUFactor, VisualFactor
- 添加完成之后调用 preMarginalize()
- 最终调用marginalize()进行边缘化
下面我们进行逐个分析。
-
ResidualBlockInfo
ResidualBlockInfo 主要保存的是每个残差块的 jacobian 和 residual,这个类的实现类似于ceres中的costfunction,同样有 Evaluate函数,参数块,残差,以及雅可比,但是其实内部的实现还是ceres中的 ceres::CostFunction* 作为参数传进来,然后在这个类的实现中进行调用。这个类的好处是可以传入各种 ceres::CostFunction* 的子类,因此也就是说可以接收IMU残差,视觉残差,先验残差等各种类型的。
其构造函数为
ResidualBlockInfo(
ceres::CostFunction *_cost_function, /// ceres 残差块
ceres::LossFunction *_loss_function, /// ceres 鲁棒核函数
std::vector<double *> _parameter_blocks, /// 构成残差需要的参数块
std::vector<int> _drop_set): /// 参数块中需要marg的变量的下标
cost_function(_cost_function),
loss_function(_loss_function),
parameter_blocks(_parameter_blocks),
drop_set(_drop_set) {}
再来看下其唯一的成员函数 Evaluate.
void ResidualBlockInfo::Evaluate()
{
/// 根据 cost-function 获得残差的维度,也就是继承时候的第一个模板参数的大小
residuals.resize(cost_function->num_residuals());
/// 获得每个参数块的大小,返回的是一个数组比如 IMUFactor : [7, 9, 7, 9]
std::vector<int> block_sizes = cost_function->parameter_block_sizes();
/// ceres 存储的是 double ** 类型的 jacobians 数据,为 raw_jacobians 分配内存空间
/// raw_jacobian 为一个过渡数据,他的值是和 jacobians 是一样的
raw_jacobians = new double *[block_sizes.size()];
jacobians.resize(block_sizes.size());
/// 遍历每个参数块
for (int i = 0; i < static_cast<int>(block_sizes.size()); i++)
{
/// 雅可比矩阵的大小等于 J_{残差维度, 参数块维度}
jacobians[i].resize(cost_function->num_residuals(), block_sizes[i]);
/// 这里绑定的是内存地址,则两个变量虽然是不同类型,但是保存的值是一样的了
raw_jacobians[i] = jacobians[i].data();
//dim += block_sizes[i] == 7 ? 6 : block_sizes[i];
}
/// 调用每个残差块自己的真正的 Evaluate 函数进行残差和雅可比的计算
cost_function->Evaluate(parameter_blocks.data(), residuals.data(), raw_jacobians);
/// 如果有核函数,则进行核函数的计算,同时也要对雅可比进行更新计算。
if (loss_function)
{
/// ..............
}
}
再来看下第二个类
-
MarginalizationInfo
先来看下里面比较重要的几个成员变量
std::vector<ResidualBlockInfo *> factors;
int m, n; /// m 为将要被marg掉的变量的维度,n为保留的变量的维度
std::unordered_map<long, int> parameter_block_size; //所有将要被marg以及和marg有关的变量的内存地址以及每个变量的维度
std::unordered_map<long, int> parameter_block_idx; //所有将要被marg以及和marg有关的变量在最终构建的H矩阵中的index,注意在刚开始的时候该成员变量存储的数据的意义会略有不同。
std::unordered_map<long, double *> parameter_block_data;//所有将要被marg以及和marg有关的变量的地址和对应的数据
其成员函数中最多被调用的为 addResidualBlockInfo(ResidualBlockInfo *residual_block_info)参数为上面我们提到的残差块。
void MarginalizationInfo::addResidualBlockInfo(ResidualBlockInfo *residual_block_info)
{
/// 添加和 marg 变量相关的残差块到成员变量的factor中去
factors.emplace_back(residual_block_info);
/// 构成残差的参数块,在正常的优化问题中也就是要优化的变量
std::vector<double *> ¶meter_blocks = residual_block_info->parameter_blocks;
/// 获得每个参数块的大小,返回的是一个数组比如 IMUFactor : [7, 9, 7, 9]
std::vector<int> parameter_block_sizes = residual_block_info->cost_function->parameter_block_sizes();
/// 遍历所有构成残差的参数块
for (int i = 0; i < parameter_blocks.size(); i++)
{
/// 得到其中一个参数的起始地址
double *addr = parameter_blocks[i];
/// 得到该参数的维度,位姿就是 7,速度和零偏就是 9,深度值就是 1
int size = parameter_block_sizes[i];
/// 将每个参数的地址和其 size 对应起来
parameter_block_size[reinterpret_cast<long>(addr)] = size;
}
/// 遍历该残差块中需要 marg 的参数
for (int i = 0; i < residual_block_info->drop_set.size(); i++)
{
/// 得到要 marg 参数在内存中的地址
double *addr = parameter_blocks[residual_block_info->drop_set[i]];
/// 要 marg 参数的地址和 idx(在A矩阵中的位置)对应(这里并没有对应,先初始化为0)
parameter_block_idx[reinterpret_cast<long>(addr)] = 0;
}
}
再来看下一个函数preMarginalize()
void MarginalizationInfo::preMarginalize()
{
/// 遍历所有和将要被 marg 掉的变量有关的残差块
for (auto it : factors)
{
/// 计算得到每个 factor 的 jacobian 和 residual (注意这里是已经优化后的残差和雅可比,是作为下一次优化的先验信息的,这里的残差按道理来说应该比较小)
it->Evaluate();
/// 遍历该 factor 的每个参数块
std::vector<int> block_sizes = it->cost_function->parameter_block_sizes();
for (int i = 0; i < static_cast<int>(block_sizes.size()); i++)
{
/// 得到参数块的地址
long addr = reinterpret_cast<long>(it->parameter_blocks[i]);
/// 得到参数块的 size
int size = block_sizes[i];
assert(size ==parameter_block_size[addr]);
// std::cout << "size: " << parameter_block_size[addr] << "; " << size << "; " << (size ==parameter_block_size[addr]) << std::endl;
/// 如果该参数块还没被插入到 parameter_block_data 中去
if (parameter_block_data.find(addr) == parameter_block_data.end())
{
double *data = new double[size];
memcpy(data, it->parameter_blocks[i], sizeof(double) * size);
/// 对参数块赋值
/// parameter_block_data 保存的是和将要被 marg 掉的变量以及相关的所有变量的地址和值的地址
parameter_block_data[addr] = data;
}
}
}
}
接下来则正式进入到 marginalize()函数
void MarginalizationInfo::marginalize()
{
int pos = 0;
/// 遍历所有被 marg 的变量
for (auto &it : parameter_block_idx)
{
/// 此时的 parameter_block_idx 第二个变量存储的是在 H 矩阵中的位置索引
it.second = pos;
pos += localSize(parameter_block_size[it.first]);
}
/// 需要 marg 掉的变量的维度
m = pos;
/// 这里的循环加上内层的判断,遍历的其实是要保留的变量
for (const auto &it : parameter_block_size)
{
/// 如果没在要 marg 的变量中找到这个地址,则说明这个地址对应的参数块是要保留的变量
if (parameter_block_idx.find(it.first) == parameter_block_idx.end())
{
/// 保存要保留变量的地址和其在H矩阵中的索引的值,这里也进行了插入操作
parameter_block_idx[it.first] = pos;
pos += localSize(it.second);
}
}
/// 需要保留的变量的维度
n = pos - m;
///
///.....................
///
}
准备 A(也就是H),b矩阵,
Eigen::MatrixXd A(pos, pos);
Eigen::VectorXd b(pos);
A.setZero();
b.setZero();
然后就是构造这两个矩阵了,作者其实是实现了两个版本,一个单线程一个多线程的,只不过作者将单线程的注释了,不过为了方便理解我们还是介绍单线程的实现,其实和多线程是一样的。
/// 遍历所有的 ResidualBlockInfo *
for (auto it : factors)
{
/// 遍历每个 ResidualBlockInfo * 的参数块
for (int i = 0; i < static_cast<int>(it->parameter_blocks.size()); i++)
{
/// 得到其在 A 矩阵中的开始位置
int idx_i = parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[i])];
/// 得到该参数的维度
int size_i = localSize(parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[i])]);
/// 得到该参数的雅可比矩阵
Eigen::MatrixXd jacobian_i = it->jacobians[i].leftCols(size_i);
/// 遍历该参数后面的参数
for (int j = i; j < static_cast<int>(it->parameter_blocks.size()); j++)
{
int idx_j = parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[j])];
int size_j = localSize(parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[j])]);
Eigen::MatrixXd jacobian_j = it->jacobians[j].leftCols(size_j);
/// 如果是对角部分
if (i == j)
A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
/// 如果不是对角部分
else
{
/// H = J^TJ
A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
/// 对称的
A.block(idx_j, idx_i, size_j, size_i) = A.block(idx_i, idx_j, size_i, size_j).transpose();
}
}
/// b = J*e
b.segment(idx_i, size_i) += jacobian_i.transpose() * it->residuals;
}
}
然后就可以开始最核心的部分了,进行边缘化
/// 矩阵左上角
Eigen::MatrixXd Amm = 0.5 * (A.block(0, 0, m, m) + A.block(0, 0, m, m).transpose());
/// 特征值分解
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);
/// 通过特征值分解求逆
Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() * saes.eigenvectors().transpose();
/// 得到每个部分,进行舒尔补
Eigen::VectorXd bmm = b.segment(0, m);
Eigen::MatrixXd Amr = A.block(0, m, m, n);
Eigen::MatrixXd Arm = A.block(m, 0, n, m);
Eigen::MatrixXd Arr = A.block(m, m, n, n);
Eigen::VectorXd brr = b.segment(m, n);
/// 先验信息 Ax=b
A = Arr - Arm * Amm_inv * Amr;
b = brr - Arm * Amm_inv * bmm;
/// 将 A 分解成 J^T * J
Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);
Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));
Eigen::VectorXd S_sqrt = S.cwiseSqrt();
Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
/// 得到 Ax=b对应的 J 和 e
linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;
再来看一下最后一个类MarginalizationFactor,继承自class MarginalizationFactor : public ceres::CostFunction。但是没有模板参数指明残差的大小以及参数块的个数和每个参数的维度,这是因为每次marg的时候是不可能事先知道的,因此这些参数都是在其构造函数中进行了指定:
MarginalizationFactor::MarginalizationFactor(MarginalizationInfo* _marginalization_info):marginalization_info(_marginalization_info)
{
/// 设置每个参数块的大小,参数块的个数当然就是mutable_parameter_block_sizes()->size()
for (auto it : marginalization_info->keep_block_size)
{
mutable_parameter_block_sizes()->push_back(it);
}
/// 设定残差块的大小
set_num_residuals(marginalization_info->n);
};
然后我们就来看一下先验残差是如何计算的,注意这里的Evaluate函数才是ceres的重写,前面那个不是的哦。
bool MarginalizationFactor::Evaluate(double const *const *parameters, double *residuals, double **jacobians) const
{
/// 保留的维度
int n = marginalization_info->n;
/// marg 的维度
int m = marginalization_info->m;
Eigen::VectorXd dx(n);
/// 遍历所有被保留的参数块
for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++)
{
/// 该参数块的 size
int size = marginalization_info->keep_block_size[i];
/// 该参数块在 A 中的大小
int idx = marginalization_info->keep_block_idx[i] - m;
/// 这个其实是已经又优化后的状态变量,parameters[i]在优化中是不断更新变动的,因为它是优化变量,也就第一次是一样的
Eigen::VectorXd x = Eigen::Map<const Eigen::VectorXd>(parameters[i], size);
/// 上一时刻的线性化点时的状态变量的值
Eigen::VectorXd x0 = Eigen::Map<const Eigen::VectorXd>(marginalization_info->keep_block_data[i], size);
if (size != 7)
dx.segment(idx, size) = x - x0;
else
{
dx.segment<3>(idx + 0) = x.head<3>() - x0.head<3>();
dx.segment<3>(idx + 3) = 2.0 * Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();
if (!((Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).w() >= 0))
{
dx.segment<3>(idx + 3) = 2.0 * -Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();
}
}
}
/// 状态变量的线性化点发生了改变,也会导致残差发生改变,因此要更新残差
Eigen::Map<Eigen::VectorXd>(residuals, n) = marginalization_info->linearized_residuals + marginalization_info->linearized_jacobians * dx;
if (jacobians)
{
/// 但是雅可比不能变,还是要用刚开始线性化点处的雅可比,因为上一个状态变量已经不在了,无法更新雅可比
for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++)
{
if (jacobians[i])
{
int size = marginalization_info->keep_block_size[i], local_size = marginalization_info->localSize(size);
int idx = marginalization_info->keep_block_idx[i] - m;
Eigen::Map<Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> jacobian(jacobians[i], n, size);
jacobian.setZero();
jacobian.leftCols(local_size) = marginalization_info->linearized_jacobians.middleCols(idx, local_size);
}
}
}
return true;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号