day09

Kmp算法

KMP的经典思想就是:当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。对比Ff算法的简单除暴，每次匹配不成功，会产生大量回溯，导致效率低下。KMP充分利用了成功匹配的部分的结果。
KMP主要应用在字符串匹配上。

KMP最重要的 就是记录已经匹配了的文本内容：next数组
next数组就是一个前缀表（prefix table）
前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。

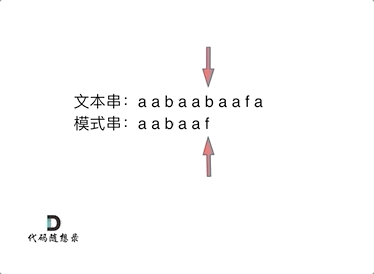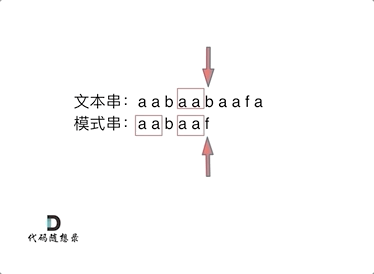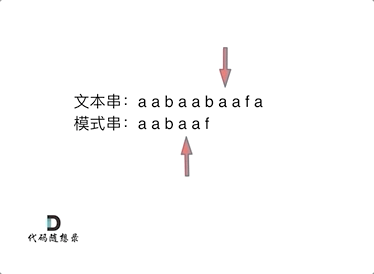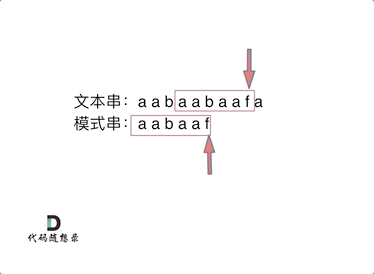
前缀表是如何记录的呢

记录的是”最长相等前后缀

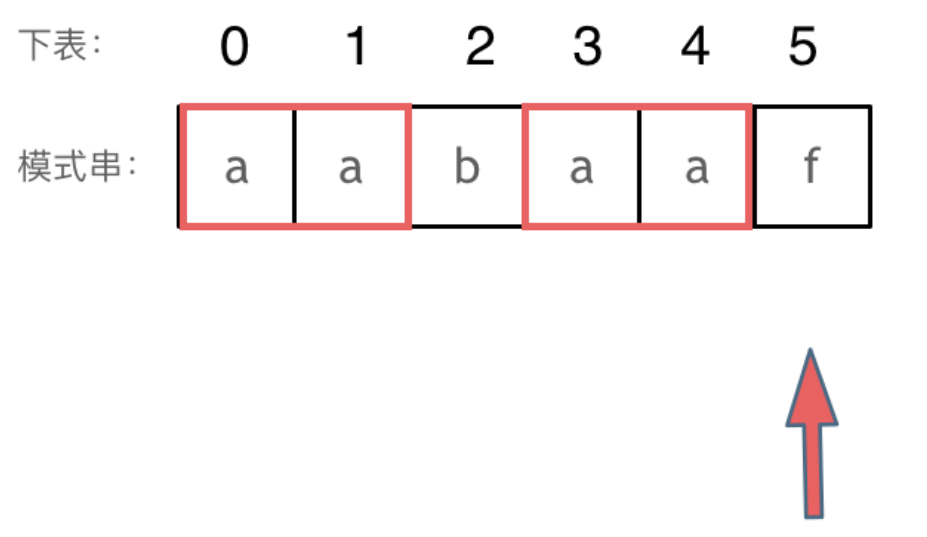
"aabaaf" 
# 前缀包含 a;aa;aab;aaba,aabaa
# 后缀包含 f;af;aaf;baaf;abaaf;
# 所以它的最长相等前后缀长度为0
 
"a" #无前缀无后缀，最长相等前后缀长度为0
"aa" #  a a 最长相等前后缀长度为1
"aab" # 最长相等前后缀长度为0
"aaba" # a  a 最长相等前后缀长度为1
"aabaa" # aa  aa 最长相等前后缀长度为2
next数组[0,1,0,1,2,0]

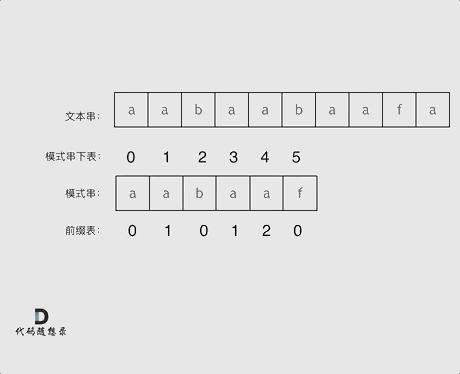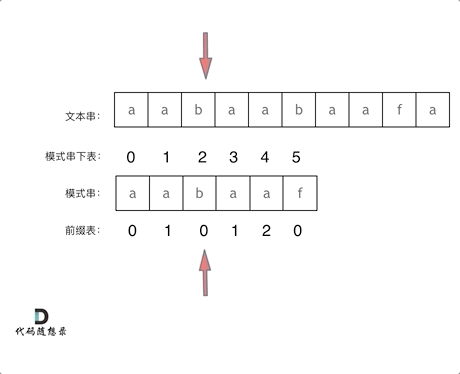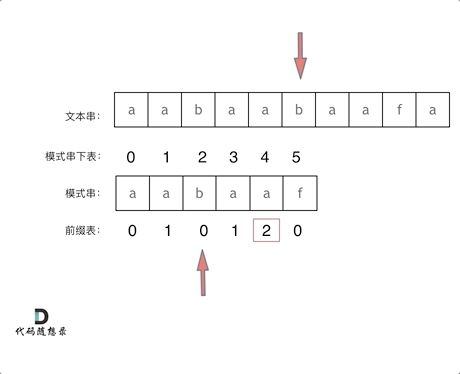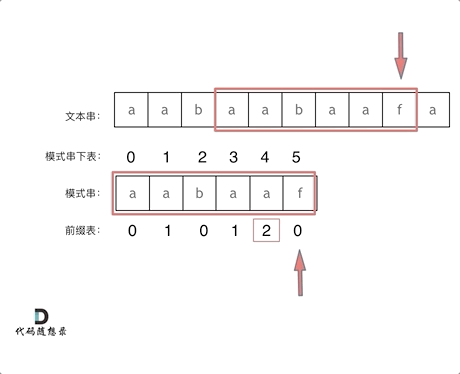
在f 发生了 冲突
1：找到发生冲突的前一个 next数组对应元素 2
2： next元素为2，说明字符串 f 之前的子串“aabaa” 的最长相等前后缀的长度为2
模式串直接跳到前缀之后 ，继续和后续比较。
这个博客写的非常易懂

https://blog.csdn.net/weixin_47284299/article/details/127104657?csdn_share_tail={"type"%3A"blog"%2C"rType"%3A"article"%2C"rId"%3A"127104657"%2C"source"%3A"weixin_47284299"}

接下来 如何实现前缀表（next数组）

肉眼看是很容易看出来next数组元素
代码如何去实现：
几个步骤：初始化，处理前后缀不同，处理前后缀相同，更新next数组
1：初始化
定义一个 指针 i j
i:指向后缀末尾位置
j：指向前缀末尾位置，也代表字串前后缀最长相等长度

void getNext(next,s){
	j=0;  //初始化
	next[0]=0;
	for(i=1;i<s.size;i++){   //处理前后最不相同情况
		while(s[i]!=s[j]&&j>0){		  //注意是while不是if  是一个连续过程  一直找到和s[i]相等  一直退到相同位置
			j=next[j-1]
		//退到相同位置后
		if(s[i]==s[j]){    //处理前后缀相同的情况
			j++;
			next[i]=j; //j就是充当计数工具，j的index就是 已经匹配的前缀长度，并且j是一开始才初始化，当i到下一个位置是，j记录的就是已经匹配好的长度
		}
			
		}
		
	}
}