构造题笔记
CF1098C Construct a tree
套用某题解的一句话:\(\color{Blue}{Rating 2300以下送命题}\)
整体思路其实很简单。
先考虑每一个节点对子树大小的贡献,为其深度。
我们二分一个 \(k\) , 线性算出满 \(k\) 叉树的子树大小和,求出使和和 \(\le s\) 的最大 \(k\) 。
然后考虑将部分节点下移,以达到加大子树大小和的目的。
\(Code:\)
#include <bits/stdc++.h>
#define int long long
#define rgi register int
using namespace std;
const int M=1e5+7,inf=1e9+7;
inline int read(){
int w=0,r=1;char c=getchar();
while(!(isdigit(c)||c=='-'))c=getchar();
if(c=='-')r=-1,c=getchar();
while(isdigit(c))w=w*10+c-'0',c=getchar();
return w*r;
}
int n,s,dep[M],cnt[M];
bool gva(int k){
int ret=s,nn=1,i=1,depp=1;
memset(cnt,0,sizeof(cnt));
for(;nn<=n;i*=k,depp++){
int x=min(n-nn+1,i);
cnt[depp]=x;
for(int j=1;j<=x;j++)dep[nn+j-1]=depp;
nn+=x;
ret-=x*depp;
}
// printf("%lld\n",ret);
if(ret<0)return 0;
nn=n;
while(ret>0){
if(cnt[dep[nn]]==1)--nn;
i=min(ret,depp-dep[nn]);
cnt[dep[nn]]--;
dep[nn]+=i;
cnt[dep[nn]]++;
ret-=i;
--nn;
++depp;
}
return 1;
}
signed main(){
n=read(),s=read();
if(s<2*n-1||s>n*(n+1)/2){
printf("No\n");
return 0;
}
printf("Yes\n");
int l=1,r=n-1,mid;
while(l<r){
mid=(l+r)/2;
// printf("%lld %lld %lld\n",l,r,mid);
int val=gva(mid);
// for(int i=1;i<=10;i++)printf("cnt[%lld]=%lld\n",i,cnt[i]);
if(!val)l=mid+1;
else r=mid;
}
// printf("%lld %lld %lld\n",l,r,mid);
gva(l);
int tot=1;
sort(dep+2,dep+n+1);
/// for(int i=1;i<=10;i++)printf("cnt[%lld]=%lld\n",i,cnt[i]);
memset(cnt,0,sizeof(cnt));
for(int i=2;i<=n;i++){
while(dep[tot]!=dep[i]-1||cnt[tot]==l)tot++;
cnt[tot]++;
printf("%lld ",tot);
}
return 0;
}
/*
4 42
6 15
32 98
*/
CF750F New Year and Finding Roots
Debug 是最寻常的,一调就是三两天。可别恼。
在用户ZHua_Lun_的帮助下,我用了五天才把这道题改出来。
我现在深刻认识到了,写题与Debug时有一个清晰的思路与沉着的猩心态是多么的重要。
回归正题。
题目内容:
- 告诉你一棵深度为 \(h(h\le7)\) 的满二叉树,节点随机编号为 \(1\sim 2^h-1\),编号不重复 。
- 你可以询问每一个节点连向哪几个节点,要求在 \(16\) 次询问内找出根节点。
刚看题目时,谁都觉得 \(16\) 个询问很难找出根节点。千万不要被吓倒。
考虑分析该二叉树中每个节点的性质。
- 1.只有一个节点与其相连,为叶节点;
- 2.有两个节点与其相连,为根节点,碰见直接输出答案;
- 3.普通的节点,有三个节点与其相连。
在这些节点中,叶节点是我们尤其需要利用的点。靠它们,我们才能让初始点不断找到自己的父亲,最终确认根节点。
我们随机从一个点(设为 \(st\))开始。
为保证每个被访问过的节点得到充分的利用,我们采用如下策略:
- \(st\) 为叶节点时,直接向上跳即可;
- 若 \(st\) 未求出深度,向三个方向进行 \(bfs\) 访问,若已求出深度则向两个未访问的方向访问;
- 访问的过程中,对于每个不为 \(st\) 的点,向一个未访问的方向访问(往更多方向延伸是没有必要的);
- 在 \(bfs\) 探索到叶节点时停止搜索,用已知信息求得 \(st\) 的深度与父节点,向上跳。
- 在 \(st\) 的深度 \(\le3\) 时特判。
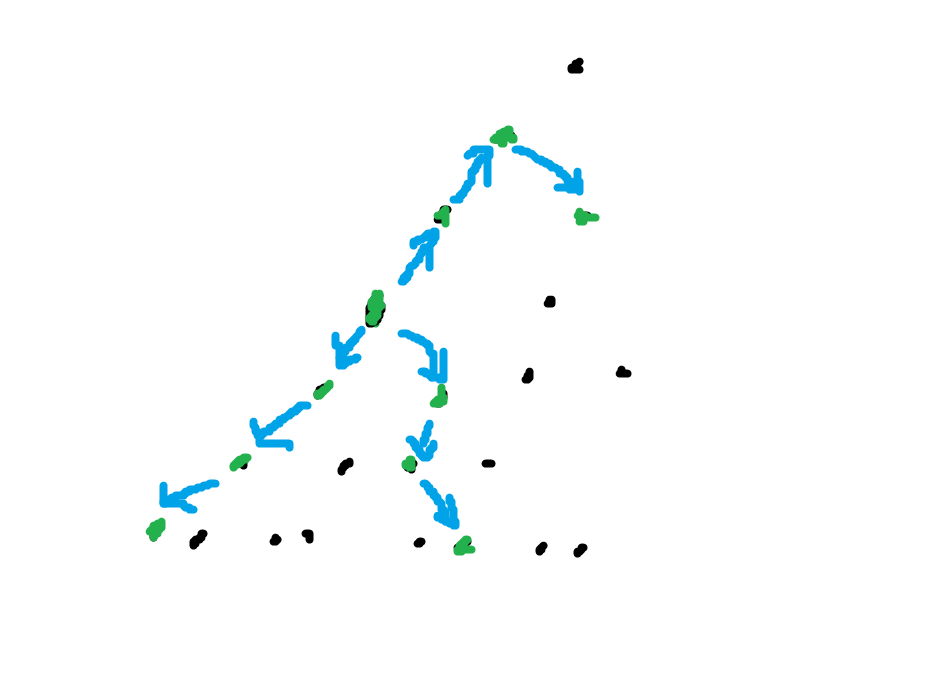
(如图,为二叉树深度为 \(7\) , \(st\) 深度为 \(4\) 时的 \(bfs\) 图)
使 \(st\) 跳跃到父节点直接所需的询问个数为\(数的深度-st的深度+1\);
所以在最坏情况下(即 \(st\) 的深度为 \(6\) 或 \(7\) 时)询问个数为 \(1+2+3+4+1+2+4=17\) 次。
还需要一个小优化:\(dep[st]==3\) 时,询问剩余 \(7\) 个点中的 \(6\) 个,若都不为根节点,则输出剩余的一个节点。
该思路即为正解。若不懂可以去看这篇博客,比我写得详细。
\(Code\)(未挖坑):
#include <bits/stdc++.h>
#define ll long long
#define rgi register int
using namespace std;
const int M=128;
inline int read(){
int w=0,r=1;char c=getchar();
while(!(isdigit(c)||c=='-'))c=getchar();
if(c=='-')r=-1,c=getchar();
while(isdigit(c))w=w*10+c-'0',c=getchar();
return w*r;
}
int fa[M],dep[M],edge[M][3],went[M],mm[M];
int dd,n,u[3],s[3];
int tedge[M][3],tmm[M];
void askk(int x,int ff){
if(went[x])return;
went[x]=1;
fa[x]=ff;
printf("? %d\n",x);
fflush(stdout);
scanf("%d",&mm[x]);
// mm[x]=tmm[x];
for(int i=0;i<mm[x];i++)scanf("%d",&edge[x][i]);
// for(int i=0;i<mm[x];i++)edge[x][i]=tedge[x][i];
}
int find1(int x,int ff){
askk(x,ff);
for(int i=0;i<3;i++)
if(fa[x]!=edge[x][i])return edge[x][i];
return edge[x][2];
}
int find2(int x,int ff){
askk(x,ff);
for(int i=2;i>=0;i--)
if(fa[x]!=edge[x][i])return edge[x][i];
return edge[x][0];
}
int bfs(int st){
// printf("quedin %d\n",st);
if(mm[st]==2)return st;
else if(mm[st]==1){
if(!dep[st])dep[st]=dd;
fa[st]=edge[st][0],askk(fa[st],st);
dep[fa[st]]=dep[st]-1;
return bfs(fa[st]);
}else{
if(!dep[st]){
for(int i=0;i<3;i++)u[i]=st,s[i]=edge[st][i];
dep[st]=dd;
while(mm[u[0]]!=1&&mm[u[1]]!=1&&mm[u[2]]!=1){
// printf("%d %d %d %d %d %d\n",u[0],u[1],u[2],mm[u[0]],mm[u[1]],mm[u[2]]);
for(int i=0;i<3;i++){
int stp=s[i];
s[i]=find1(s[i],u[i]);
u[i]=stp;
if(mm[u[i]]==2)return u[i];
}
dep[st]--;
}
for(int i=0;i<3;i++)
if(mm[u[i]]==3){
fa[st]=edge[st][i];
break;
}
dep[fa[st]]=dep[st]-1;
return bfs(fa[st]);
}
else if(dep[st]==2){
int a1=find1(st,fa[st]),a2=find2(st,fa[st]);
askk(a1,st);
if(mm[a1]==2)return a1;
else return a2;
}
else if(dep[st]==3){
int a1=find1(st,fa[st]),a2=find2(st,fa[st]);
int b1=find1(a1,st),b2=find2(a1,st),b3=find1(a2,st),b4=find2(a2,st);
askk(b1,a1),askk(b2,a1),askk(b3,a2);
if(mm[b1]==2)return b1;
else if(mm[b2]==2)return b2;
else if(mm[b3]==2)return b3;
else return b4;
}
else{
for(int i=0;i<2;i++)u[i]=st;
s[0]=find1(st,fa[st]),s[1]=find2(st,fa[st]);
for(int j=1;j<=dd-dep[st];j++){
// printf("2\n");
for(int i=0;i<2;i++){
int stp=s[i];
s[i]=find1(s[i],u[i]);
u[i]=stp;
if(mm[u[i]]==2)return u[i];
}
}
if(mm[u[0]]==3)fa[st]=find1(st,fa[st]);
else fa[st]=find2(st,fa[st]);
dep[fa[st]]=dep[st]-1;
return bfs(fa[st]);
}
}
}
signed main(){
int t;
scanf("%d",&t);
while(t--){
memset(fa,0,sizeof(fa));
memset(dep,0,sizeof(dep));
memset(edge,0,sizeof(edge));
memset(went,0,sizeof(went));
memset(mm,0,sizeof(mm));
dd=read();
n=(1<<dd)-1;
/*for(int i=1;i<n;i++){
int fr=read(),tr=read();
tedge[fr][tmm[fr]++]=tr,tedge[tr][tmm[tr]++]=fr;
}
for(int i=1;i<=n;i++){
printf("***%d %d ",i,tmm[i]);
for(int j=0;j<tmm[i];j++)printf("%d ",tedge[i][j]);
printf("\n");
}*/
if(dd<=4){
for(int i=1;i<=n;i++){
printf("? %d\n",i);
fflush(stdout);
int x,y;
scanf("%d",&x);
for(int j=1;j<=x;j++)scanf("%d",&y);
if(x==2){
printf("! %d\n",i);
fflush(stdout);
break;
}
}
}
else{
askk(1,0);
printf("! %d\n",bfs(1));
fflush(stdout);
}
}
return 0;
}
/*
15
6
39 60
39 59
60 36
60 42
59 52
59 18
36 54
36 28
42 51
42 47
52 1
52 27
18 14
18 13
54 23
54 21
28 25
28 20
51 2
51 16
47 17
47 6
1 61
1 3
27 31
27 55
14 4
14 41
13 24
13 32
23 63
23 12
21 11
21 15
25 35
25 38
20 48
20 33
2 50
2 22
16 40
16 29
17 7
17 45
6 26
6 43
61 8
61 53
3 5
3 10
31 46
31 58
55 19
55 44
4 34
4 57
41 30
41 56
24 49
24 37
32 62
32 9
*/



 浙公网安备 33010602011771号
浙公网安备 33010602011771号