权重随机算法的java实现

一、概述

　　平时，经常会遇到权重随机算法，从不同权重的N个元素中随机选择一个，并使得总体选择结果是按照权重分布的。如广告投放、负载均衡等。

　　如有4个元素A、B、C、D，权重分别为1、2、3、4，随机结果中A:B:C:D的比例要为1:2:3:4。

　　总体思路：累加每个元素的权重A(1)-B(3)-C(6)-D(10)，则4个元素的的权重管辖区间分别为[0,1)、[1,3)、[3,6)、[6,10)。然后随机出一个[0,10)之间的随机数。落在哪个区间，则该区间之后的元素即为按权重命中的元素。

　　实现方法：

利用TreeMap，则构造出的一个树为:
　　　　B(3)
　　　 /      \
        /         \
     A(1)     D(10)
               /
             /
         C(6)

然后，利用treemap.tailMap().firstKey()即可找到目标元素。

当然，也可以利用数组+二分查找来实现。

请尊重作者劳动成果，转载请标明原文链接：https://www.cnblogs.com/waterystone/p/5708063.html

二、源码

package com.xxx.utils;

import com.google.common.base.Preconditions;
import org.apache.commons.math3.util.Pair;
import org.slf4j.Logger;
import org.slf4j.LoggerFactory;

import java.util.List;
import java.util.SortedMap;
import java.util.TreeMap;

public class WeightRandom<K,V extends Number> {
    private TreeMap<Double, K> weightMap = new TreeMap<Double, K>();
    private static final Logger logger = LoggerFactory.getLogger(WeightRandom.class);

    public WeightRandom(List<Pair<K, V>> list) {
        Preconditions.checkNotNull(list, "list can NOT be null!");
        for (Pair<K, V> pair : list) {
            Preconditions.checkArgument(pair.getValue().doubleValue() > 0, String.format("非法权重值：pair=%s", pair));

            double lastWeight = this.weightMap.size() == 0 ? 0 : this.weightMap.lastKey().doubleValue();//统一转为double
            this.weightMap.put(pair.getValue().doubleValue() + lastWeight, pair.getKey());//权重累加
        }
    }

    public K random() {
        double randomWeight = this.weightMap.lastKey() * Math.random();
        SortedMap<Double, K> tailMap = this.weightMap.tailMap(randomWeight, false);
        return this.weightMap.get(tailMap.firstKey());
    }

}

 

测试CASE：

public class WeightRandomTest {
    List<Pair<String, Integer>> list;
    private WeightRandom<String, Integer> random;
    private Logger logger = LoggerFactory.getLogger(this.getClass());


    @Test
    public void random() {
        Map<String, Integer> countMap = Maps.newHashMap();
        for (int i = 0; i < 100000000; i++) {
            String randomKey = random.random();
            countMap.put(randomKey, countMap.getOrDefault(randomKey, 0) + 1);
        }

        for (Pair<String, Integer> pair : list) {
            logger.debug("{}:{}", pair.getKey(), countMap.get(pair.getKey()));
        }
    }

    @Before
    public void init() {
        list = Lists.newArrayList();
        list.add(new Pair("A", 1));
        list.add(new Pair("B", 2));
        list.add(new Pair("C", 3));
        list.add(new Pair("D", 4));
        list.add(new Pair("E", 0));

        this.random = new WeightRandom(list);
    }

}

 

三、性能

4个元素A、B、C、D，其权重分别为1、2、3、4，运行1亿次，结果如下：

元素	命中次数	误差率
A	10004296	0.0430%
B	19991132	0.0443%
C	30000882	0.0029%
D	40003690	0.0092%

从结果，可以看出，准确率在99.95%以上。

 

四、另一种实现

利用B+树的原理。叶子结点存放元素，非叶子结点用于索引。非叶子结点有两个属性，分别保存左右子树的累加权重。如下图：

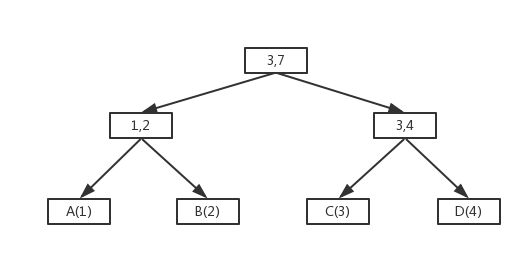
看到这个图，聪明的你应该知道怎么随机了吧。

此方法的优点是：更改一个元素，只须修改该元素到根结点那半部分的权值即可。

end