拜线段树

目录

• 线段树
  • 线段树基础
    • 猫树
  • 普通线段树应用
  • 值域线段树
  • 可持久化线段树
    • 势能分析
  • 吉司机线段树
  • 扫描线
    • 区间问题的反演
    • 换维扫描线
  • 历史和
  • 线段树分裂/合并
    • 单侧递归
  • 李超线段树

线段树

线段树初学者勿入。重新整理一下线段树。可能在后续会陆陆续续地添加一些拓展或者题目。

画线段树的网站 (Segment Tree) - VisuAlgo

线段树基础

线段树是每个节点代表一个区间构成的二叉树结构。

线段树的本质就是大区间的信息代表两个小区间信息合并的信息。

普通线段树就不说了。看看线段树还可以在那些地方做文章。

• 节点的编排顺序

直接编号会发现叶子节点的编号可能不连续，于是空间需要开 4 倍，但是线段树明明只有 2n 的节点。

查理线段树：可以把一个节点的左儿子编号为 mid * 2，右儿子编号为 mid * 2 + 1。可以发现，每个区间的 mid 必然不同，所以不同区间的儿子编号必然不同，除了根节点，每个节点都是作为另一个节点的儿子出现，所以只用把根节点编号为 1 就没有区间编号重了。最大的 mid 是 n - 1（不给叶子的儿子编号），那么节点的最大编号为 \((n-1)*2-1=2*n-1\)，刚好是节点数，这样就没有浪费空间了。

有些时候值域很大，可离线的话可以离散化一下，如果不行使用动态开点线段树解决。

• 递归改为非递归

众所周知，递归常数大。那么线段树是否可以非递归？这就是重口味 zkw 线段树。

总体来说，zkw 线段树与普通线段树最大的区别就是一个是递归一个是递推，然后 zkw 的编号方式也有一点点不同。

普通线段树叶子节点的编号很乱，zkw 的编号方式就略有不同。设 \(N=2^{\left \lfloor \log_2 n \right \rfloor }\) ，原序列第 i 个数对应的叶子节点为 \(i+N\)，然后新填两个节点，0 号节点和 n+1 号节点，然后在这上面建线段树。每个节点的父亲的编号都是儿子编号的一半。（如果不向 2 的次幂取整，就会导致 2 号节点的儿子是 4 和 5，但是这两个节点代表的可能不是连续的区间，感觉有点麻烦，如果是 N 是 2 的整数幂，那么最左边的路径上的数就都是 2 的整数倍，4 和 5 肯定就是同一层的连续区间了）

以一个 [1,4] 的区间为例，这是它的 zkw，

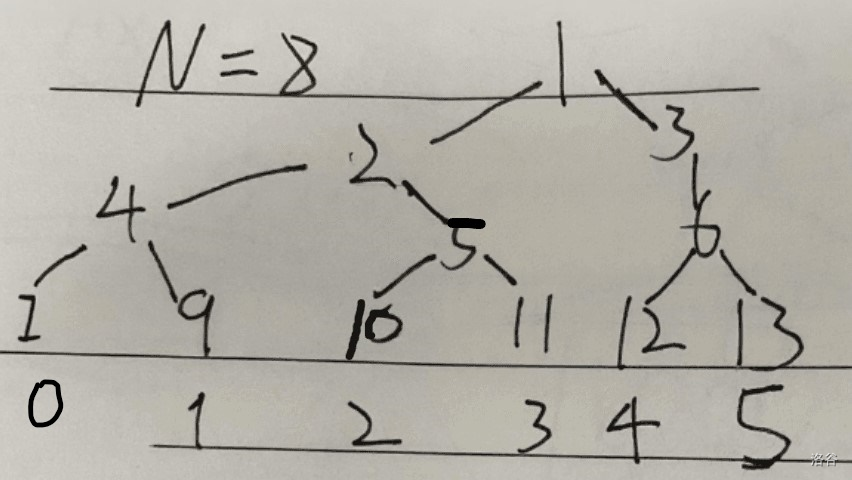
考虑如何不递归地定位区间。

有一个非常人类智慧的做法：对于区间 \([l,r]\) 找到 \(l - 1\) 和 \(r + 1\) 的根链，两条根链中间的大区间就是目标区间。这和递归线段树找到的区间是一摸一样的。然后改打标记打标记，改求和求和。这就是 zkw 线段树的核心思想。

这是它定位区间 [2,4] 的过程，最后找到了 5 号和 12 号节点，

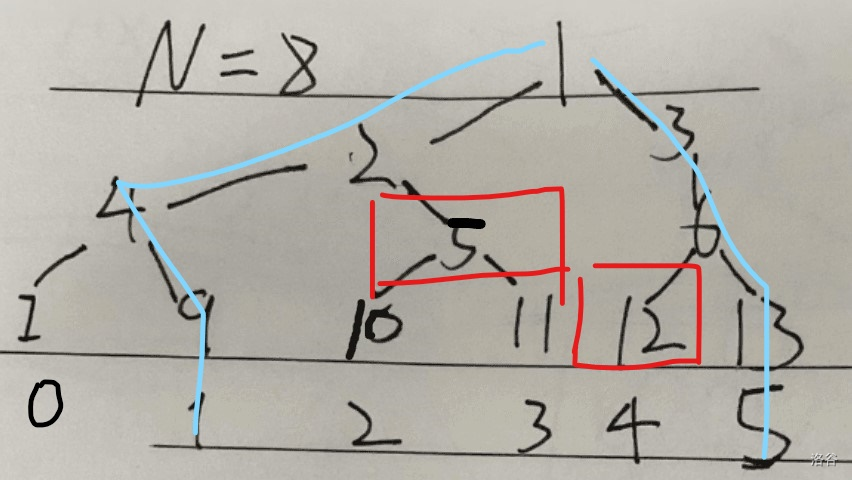
以 modify 为例，

inline void mdf(int l, int r, ll a, ll b) {
    l += nn - 1, r += nn + 1, push_down(l), push_down(r); // 必须把从根往下的 tag 先铺平
    while(l ^ r ^ 1) {// l 和 r 的父亲节点不同，如果相同，l r 只有最后一位相差1
        if(~l & 1) upd(l ^ 1, a, b); // 如果是左儿子，就区间加右儿子
        if(r & 1) upd(r ^ 1, a, b); // 同上
        l >>= 1, r >>= 1, up(l), up(r); // 勿忘 up
    }up(r); while(l) up(l), l >>= 1; // 必须让上面的节点是对的
}

具体来说，

现在还有一个问题，就是祖先节点上可能有标记，但是用这个方法找区间的过程很有可能根本不会下放这些祖先节点的标记，所以开始找区间之前，要先从上到下把 \(l - 1\) 和 \(r + 1\) 的根链上的标记下传了。

现在还有一个问题，就是如果直接按照上述方法实现的话，求区间和的时候，这个区间可能还没被 push_up，也就是儿子节点的值在之前区间加了，但是祖先还没有更新。这其实只需要在找到区间以后一路 push_up 上去就行了。

比递归版快了 4 倍多，冲进了最优解第二页。

线段树2 提交记录

似乎还有一个两倍空间的混沌邪恶 zkw 写法，我研究了很久都没懂。如何写出简单又强势的线段树 - 洛谷专栏。

• 广义线段树

也就是不在中点处划分左右区间。

用处：可以在 mid 向上取 2 的整数次幂，这样复杂度也是对的，不过可拓展性弱，似乎没什么用。还用一个用处就是来出各种混沌邪恶题目，让你维护一个 xjb 乱划分左右区间的线段树。

然而 zkw 的这种思想非常的牛逼，有些时候甚至可以用来做广义线段树的邪恶题目：

例题：校门外歪脖树上的鸽子（某邪恶联考题）可以通过这个读题

大意是区间加区间求和的广义线段树，但是不下传标记，然后问你询问的答案在这种写法下是多少。

按照 zkw 的思想，找到 l - 1 和 r + 1 的根链，对于 l - 1 的根链，统计在它是左儿子时统计右儿子的答案，r + 1 的根链统计它是右儿子时左儿子的答案。如果你理解了 zkw 线段树，这是显然的。所以问题变成了树链打加法标记，树链求和，注意这里的树链求和指的是对区间标记乘上一个关于深度的系数后的和。然后就可以用数剖线段数做了。

zkw 优势：好写，常数小。zkw 劣势：不能动态开点。

猫树

参考：一种神奇的数据结构——猫树 - 洛谷专栏。

用处：满足结合律且支持快速合并的信息，如区间和，区间最大子段和。不过如果是可以差分的信息肯定就直接维护前缀然后差分来做了，猫树做的是合并容易差分难的静态问题。

复杂度：预处理 \(O(n\log n)\)，询问 \(O(1)\)，空间 \(O(n\log n)\)，单点修改 \(O(n)\) ，区间修改 \(O(n\log n)\) （区间修改相当于重构树）

可以看出，猫树不支持修改！

• 大体思路

想办法把询问区间拆成只拆成两个预处理过的区间，问题就在于如何在一个较短的时间内预处理区间信息，并且使得任意一个区间都能被分成两份预处理过的区间。

• 正文

其实就是分治，按照类似线段树的方法分治。对于线段树每个节点代表的区间，为了维护跨过 mid 的答案，维护一个左区间的后缀信息和右区间前缀信息。这样就能把任意询问区间分成两个被预处理过的区间。

以区间求和为例，

对于左边的区间，i 倒序遍历， \(f[i]=f[i+1]+a[i]\)

对于右边的区间，i 正序遍历， \(f[i]=f[i−1]+a[i]\)

因为除了长度为 1 的区间，定位任意一个区间在线段树递归过程中，一定有一次能被分成两个区间继续递归，这就是我们要找的位置。

（偷的图）例如红色区间，就会递归到这里的时候被处理。

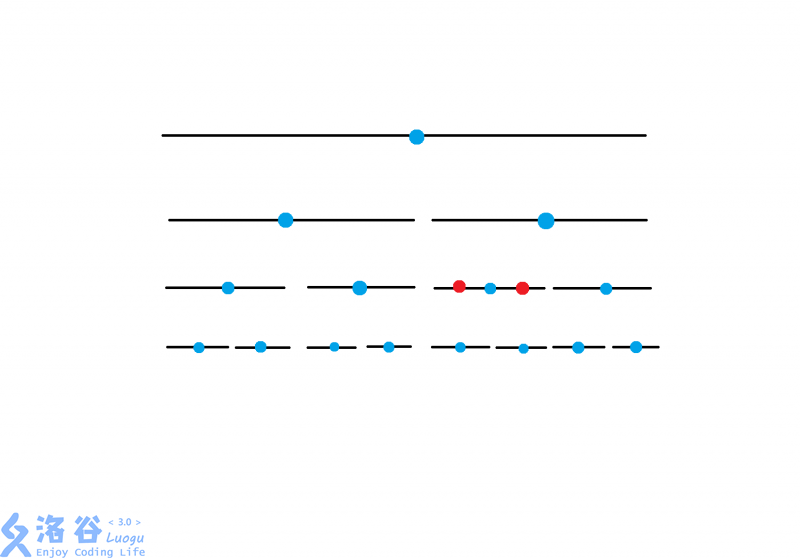
但是如果直接递归地找到这个区间是 \(O(\log n)\) 的，但是通过人类智慧，我们发现这个区间正好就是询问的 l，r 对应的两个叶子节点它们的 LCA ！

这时候可以使用 \(O(1)LCA\) 解决问题，但是又通过人类智慧，我们发现这个节点的深度是 l 和 r 编号在 0-index 下二进制的最长公共前缀的长度。例如 001 和 011，lca 离叶子的距离是 2。

以SP1043 GSS1 - 静态最大子段和为例的代码，有一种非递归 NTT 的美感：

int n, m, a[N], H[N * 2];
struct node{
	int s, sf, pr, sb; // sb is max sum of subsequence
	inline node operator + (const node & v) {
		node tmp; tmp.s = s + v.s, tmp.pr = max(pr, s + v.pr), tmp.sf = max(v.sf, v.s + sf), tmp.sb = max({sb, v.sb, sf + v.pr});
		return tmp;
	} // 注意加的顺序，没有交换律
	inline node (int x = 0) : s(x), sf(x), pr(x), sb(x) {}
}val[N], ct[Ln][N]; // val 是叶子节点
void bt() {
	For(i, 1, n) val[i - 1] = node(a[i]);
	For(i, 1, n * 2) H[i] = __lg(i);
	for(int h = 0, len = 2; len < n * 2; len <<= 1, ++ h) 
		for(int l = 0, mid = (len >> 1) - 1, r = len - 1; mid < n - 1; l += len, mid += len, r += len) {
			r = min(r, n - 1);
			ct[h][mid] = val[mid], ct[h][mid + 1] = val[mid + 1];
			for(int i = mid - 1; i >= l; -- i) ct[h][i] = val[i] + ct[h][i + 1];
			for(int i = mid + 2; i <= r; ++ i) ct[h][i] = ct[h][i - 1] + val[i];
		}
} // 为了方便求 lca 节点，使用的是 0-index
inline int ask(int l, int r) {
	if(l == r) return a[l]; // 记得特判叶子节点
	-- l, -- r; return (ct[H[l ^ r]][l] + ct[H[l ^ r]][r]).sb;
}

注意：下标从 0 开始才方便找 lca

普通线段树应用

• 满足结合律且支持快速合并的信息，如区间和，区间 max，min，区间 gcd，区间最大子段和，甚至矩阵，置换皆可维护。可以带修，可以打标记的操作，如区间加乘，区间推平。不能拘泥于背这些操作，要思考题目中要维护的东西满不满足这些性质。

单点加的话一般用树状数组，某些特殊的单点修改和信息用 zkw 很好写，优势在于打标记。

如果有多个操作，要考虑操作该如何合并。

• 线段树上二分

需要对一个区间，查找第一个满足某个性质的东西。把区间对应的线段树节点找到，按顺序查找目标在那个节点，然后递归这个节点，复杂度 \(O(\log n + \log n) = O(\log n)\)​ ，比直接做快。

• 树剖线段树

树剖以后子树的 dfs 序是一个区间，链的 dfs 序是 log 个连续区间，用线段树维护信息。当然也可以用其他数据结构维护。

• 线段树优化 dp

就是 dp 转移有区间求和，区间推平一类的东西，就用线段树维护。

• 优化建图

这都算是图论的东西了。

比如现在要让 x 节点连向编号在 \([l,r]\) 中的节点，直接连边数爆炸，所以建以颗线段树，每个节点向儿子节点连边，叶子节点是原图中的节点，然后 x 就只用连向区间在线段树上对应的那些节点即可。

值域线段树

就是把值域当成下标开线段树。

是一个换维的思想，有时候有妙用。

比如要动态求 \(\sum \min(a_i,a_j)\) 的时候，可以使用值域线段树，对于每个 \(a_i\) 的贡献就是值域上大于 \(a_i\) 的数的个数，在值域线段树上比较好统计。

可持久化线段树

可持久化的根本。

直接复制一遍原来的数组 / 线段树非常砸缸，所以只维护修改了的地方。

可持久化原则：修改不能修改，必须变成复制原来的节点，然后修改复制出来的节点。具体实现类似于动态开点线段树。

• sm 题目不让你离线，于是要在线解决一些动态问题，有些询问可能需要回溯到之前的位置。

• 需要维护一个动态的数组，但是有回溯操作。

• 查询一个前缀信息的问题。

一个一个地插入每个数，然后对于不同的 \(r\)，认为 \([1,r]\) 是一个历史版本，每次查询到对应版本即可。当然，如果条件允许，应该直接对 \(r\) 扫描线。

• 查询区间中 x 的前驱后继（经典例题）

用可持久化值域线段树，把 r 的限制可持久化掉。对于前驱，找到 \([1,r]\) 的历史版本，就是在值域 \([1,x]\) 中，找到最靠右的下标大于 \(l\) 的数，在值域上开线段树的话，这个问题就转化为了二分找后缀 max 大于 \(l\) 的位置。对于后继，在维护一颗可持久化值域线段树，然后把权值改为 inf - val[i] + 1。

• 一些树上问题，需要维护每个节点的线段树
• 用主席树维护二进制数

进位是一个线段树二分和区间覆盖。

注意到，修改操作多的时候，空间巨大，根据需要定期重构。缺点在于空间消耗和常数。

势能分析

例如取模操作，如果取模成功，这个数一定至少减半，只要没有区间加（或者其他让一堆数突然变大的操作），就可以暴力找到每个值会改变的地方，然后单点修改。找数的过程通常维护一个区间 max。类似可维护的操作有gcd. 例题：[P9989 Ynoi Easy Round 2023] TEST_69 - 洛谷

吉司机线段树

用处，对一个区间，让这个区间于某个数取 min，并且同时要维护加操作。单点修改的话是 \(O(\log^2n)\) 区间修改的话是 \(O(\log^3n)\).

本质上是势能分析。维护一个区间 mx 和次大值 smx ，当 v 大于 smx 是好做的，当它小于(严格小于) smx 时暴力递归更新。分析出来就是这个复杂度。

扫描线

就是枚举某一维，只用维护这其他维的变化，可以降维。

lxl 名言

1. 扫描线是将静态的高自由度问题转换为动态的低自由度问题的方式。
2. 扫描线扫不同的维，扫不同的方向，会将原静态问题转换为不同形式的动态问题。

区间问题的反演

对于询问区间答案的题目，我们反过来考虑点对区间的贡献。具体来说，我们建立以区间左端点 l

为横坐标，r 为纵坐标的平面，这样区间就转化成了平面的点。而包含某一个点的区间会组成一个2-side的矩形，计算点对区间的贡献只用对这个矩形做操作就行了。

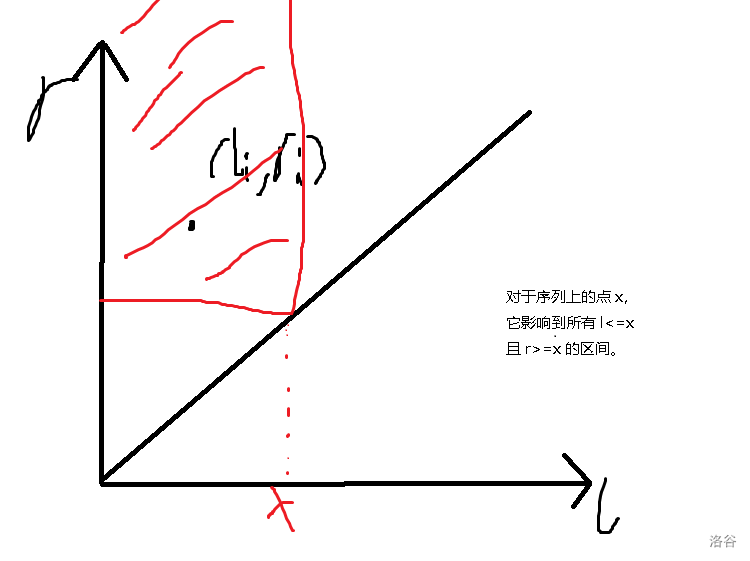
用处：

• 可以二维数点。
• 处理区间子区间

换维扫描线

现在开一个时间维，扫描线扫序列，数据结构维护时间。例题

显然，扫描线其实不一定要用线段树维护。

历史和

可用于矩形求和。

矩形直接扫描线求和一看就非常难做。树套树太慢了。

对于 4-side 矩形直接差分成 3-side 矩形，然后求这个 3-side 矩形内区间加标记的面积。

比如蓝色矩形被差分成了两个绿色矩形。对于深绿色矩形，它的答案是这些红色区间加标记的面积。

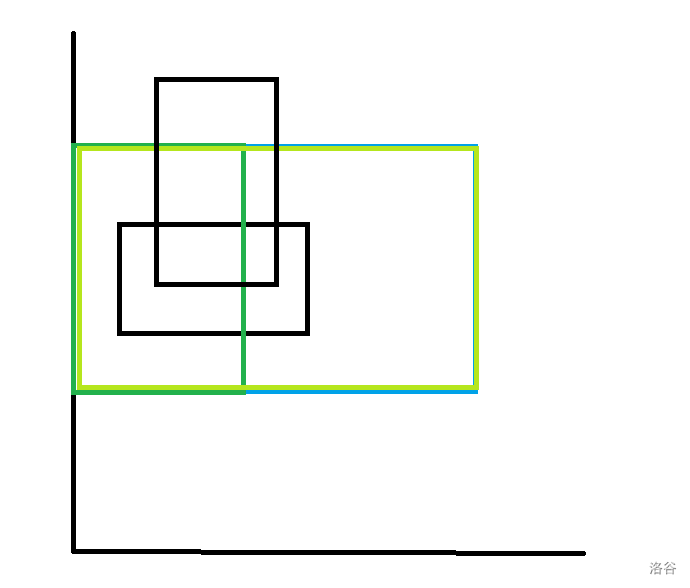
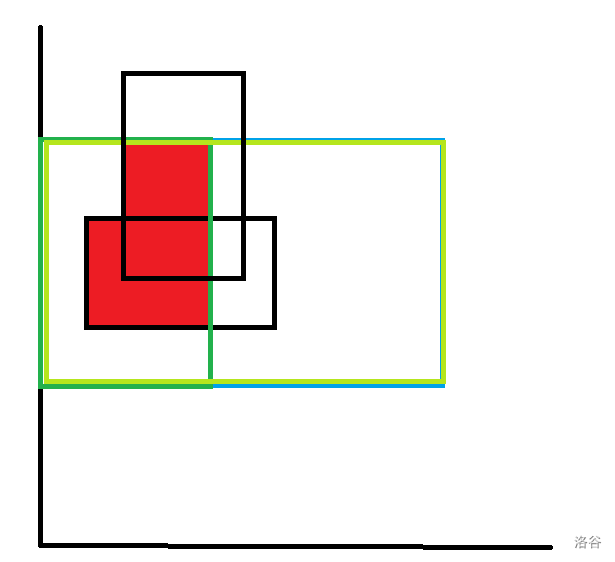
我们用线段树a来表示扫描线维护需要的线段树，这个线段树维护的是真实的区间。

用线段树b来表示历史和区间，表示从刚开始到扫描线的位置，所有的区间加的面积。

假设某一个区间加标记大小为x距离下一个区间加标记的时间跨度是 h，那么历史和线段树就要对加的这个区间加上 \(x\times h\)。 这时候，我们打一个历史和标记 h（ ，下一次要先加历史和再区间加。？）

还有一些普通的a的区间加。合并标记的时候发现历史和标记会对之前的区间加产生一个历史和的区间加。

现在有三种标记：a对b的历史和，a的区间加，b的区间加。

合并 hA aB bC , hD aE bF => h(A+D) a(B+E) b(C+F+DB)

还有一种合并方法是：

对于区间合并：

\[\begin{bmatrix} 1& 0&0 \\ 1& 1&0 \\ 0& 0&1 \end{bmatrix} \begin{bmatrix} suma\\sumb\\len \end{bmatrix} = \begin{bmatrix} suma'\\sumb'\\len \end{bmatrix} \]

对前面的矩阵求h次方就是历史和。

\[\begin{bmatrix} 1& 0&A \\ 0& 1&0 \\ 0& 0&1 \end{bmatrix} \begin{bmatrix} suma\\sumb\\len \end{bmatrix} = \begin{bmatrix} suma'\\sumb'\\len \end{bmatrix} \]

这个就是区间a加A

核心是多维护一个离上次更新历史和的时间标记，只要想清楚标记怎么合并的就行

线段树分裂/合并

分裂不会，似乎用处不大。实在不行就写平衡树吧。。。

对于合并，使用动态开点线段树：

我们通过以下过程来将两个线段树节点 u,v 合并，并以 u 作为新的根。

• 如果 v 为空，结束过程。
• 如果 u 为空，将 v 复制给 u。
• 递归将 u,v 的左右子树对应合并。

就是 TM 暴力剪枝。

复杂度。如果合并两个 n 个节点的线段树，就是 \(O(n\log n)\)。但是一般线段树合并都是合并权值线段树，并且总共有 n 个有效权值。

复杂度证明：如果遍历到某个 u v 都有的节点，发现上述过程相当于删掉了 v 中的节点，如果 u v 之中只有一个在某个位置拥有节点，那么就不会继续搜索下去，而且只有删除了节点才会多搜到这种节点。所以说，删除节点个数与遍历次数同阶。加入一个数（或权值）会导致添加 log 个节点，复杂度等于删除节点个数等于添加节点个数等于 \(O(n\log n)\).

在很多树上统计一些信息的问题里，尤其针对于在每个节点都有信息要统计时，使用 DSU 套数据结构往往是两个 log ，如果没有特殊的限制，线段树合并能做到单 log ，如果之后每个节点都有用，（比如一些 sm 换根题目），则需要可持久化。

例题

注意，如果一个线段树被合并以后就没用了，就用普通动态开点线段树即可。但如果合并以后，仍然可能会被遍历，则需要可持久化线段树。

应用

• 各式各样的树上合并问题
• 维护二进制数
• SAM 维护每个等价类对应的 endpos 集合

单侧递归

有些信息不好直接合并，但是如果可以通过只递归左右子区间的其中之一来实现，可以使用单侧递归。

例如：区间多少位置是区间的前缀最大值。例题.

每个区间维护两个信息，区间的答案 ans 和区间 max，最大值非常好维护，考虑如何合并 ans。

首先左区间的 ans 肯定不会变，然后分讨右区间 max 是否大于左区间，如果小于，那么没有贡献。

如果大于左区间，那么递归右区间，然后比较右区间的左子区间与左区间的大小关系。

如果左区间 max 大于左子区间，那么只用递归右子区间。

否则，左区间的对右子区间的影响弱于左子区间对右子区间的影响，右子区间的答案就是受左子区间影响以后的右区间，就是大区间的 ans 减左区间的 ans，递归左子区间。用 zkw 实现很好写，常数还小。

李超线段树

大量参考，代码

作用：

• 加入一个一次函数，定义域为 [l,r]；
• 给定 k，求定义域包含 k 的所有一次函数中，在 x=k 处取值最大的那个，如果有多个函数取值相同，选编号最小的。

李超线段树使用条件：任意两函数之间最多只能有一个交点。大部分情况下李超线段树维护的是直线。一些其他的某些函数，可以拆成多个单调的函数，然后用李超线段树维护。

李超线段树的每一个节点维护所有经过该值域区间中点的线段中，函数值在区间中点取值最大的函数的解析式。

加入函数部分分成两步

1. 把函数定义域分解成线段树的区间。
2. 对于每个部分去更新维护的线段。

具体来说，设当前区间的中点为 m，我们拿新线段 f 在中点处的值与原最优线段 g 在中点处的值作比较。

如果新线段 f 更优，则将 f 和 g 交换。那么现在考虑在中点处 f 不如 g 优的情况：

• 若在左端点处 f 更优，那么 f 和 g 必然在左半区间中产生了交点，f 只有在左区间才可能优于 g，递归到左儿子中进行下传；
• 若在右端点处 f 更优，那么 f 和 g 必然在右半区间中产生了交点，f 只有在右区间才可能优于 g，递归到右儿子中进行下传；
• 若在左右端点处 g 都更优，那么 f 不可能成为答案，不需要继续下传。

除了这两种情况之外，还有一种情况是 f 和 g 刚好交于中点，在程序实现时可以归入中点处 f 不如 g 优的情况，结果会往 f 更优的一个端点进行递归下传。

第二步应该可以非递归。

合并（还没写过）

类似于普通线段树的合并，我们定义以下过程来将两个李超线段树节点 u,v 合并，并以 u 作为新的根。

• 如果 v 为空，结束过程。
• 如果 u 为空，将 v 复制给 u。
• 将 v 对应线段插入到 u 为根的子树。
• 递归将 u,v 的左右子树对应合并。