高级数据结构

一、线段树

二、树状数组

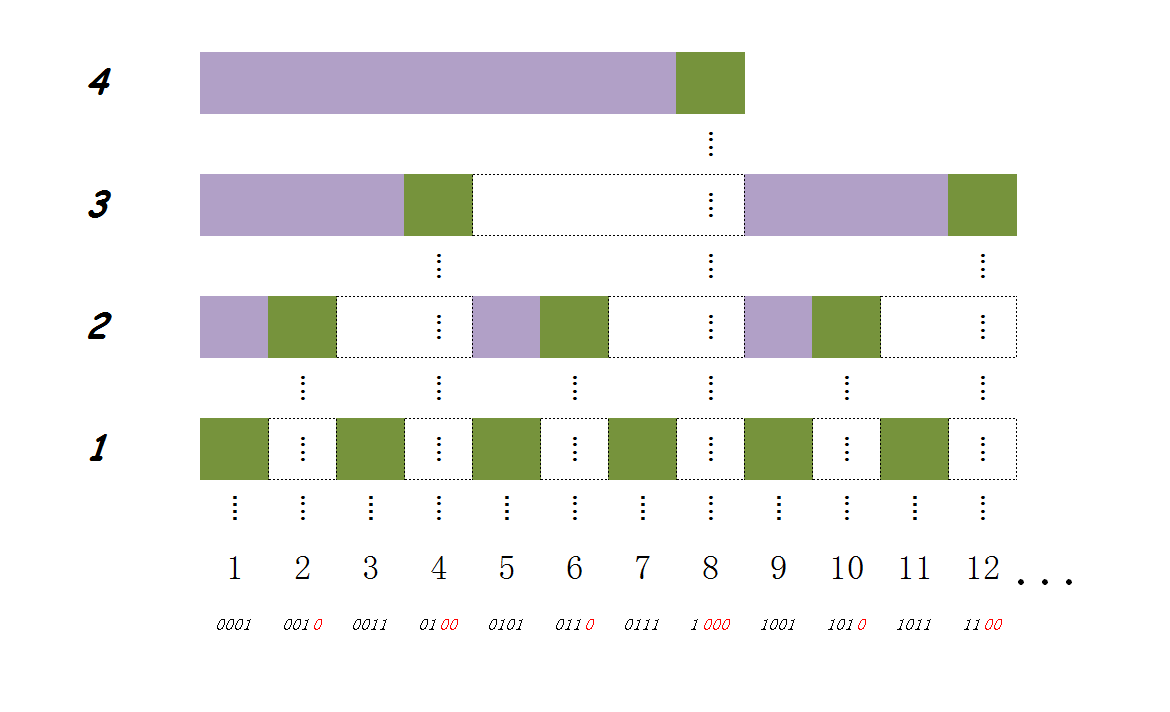
原理

• 我们通过观察这张图可以发现如下性质：
  • 后缀和的长度是 \(2\) 的幂。
  • 上一层后缀和的长度是下一层的 \(2\) 倍。
  • 下面一层只要补上自己的后缀和长度就可以得到上面层的后缀和的长度（即虚线框）。

1. 单点修改

• 从树状数组的原理我们可以看出，假如我们修改一个点的值，则会影响到所有覆盖有该点的线段。例如，我们想修改0011的话，不光会改变其自生的值，还会影响到0100和1000的线段。

2.区间求和

• 给出 \([left,right]\) 区间，求该区间的和。我们可以分别求出 \(Sum_{left-1}\) 和 \(Sum_{right}\) 然后相减。\(Sum_{x}\) 为 \(x\) 所有 \(lowbit(x)\) 段的和。

代码实现

#define lowbit(x) (x&(-x))
class BIT {
private:
	vector<int> tree;
public:
	BIT(int n) :tree(n + 1) {}
	void add(int k, int x) {
		while (x < tree.size()) {
			tree[x] += k;
			x += lowbit(x);
		}
	}
	int query(int x) {
		int ret = 0;
		while (x) {
			ret += tree[x];
			x -= lowbit(x);
		}
		return ret;
	}
	int sum(int left, int right) {
		return this->query(right) - this->query(left);
	}
};

使用树状数组两种情况

• 单点修改与区间求和
• 区间修改与单点查询——在建树的时候使用差分思想。

void add(int pos,int x){
    while(pos<=n) delta[pos]+=x,pos+=lowbit(pos);
}
void modify(int l,int r,int x){
    add(l,x),add(r+1,-x);
}
int getsum(int pos){
    int sum=0;
    while(pos) sum+=delta[pos],pos-=lowbit(pos);
    return sum;
}

进阶

• 我们可以用树状数组实现丐版线段树（实现区间修改&区间查询）

#define lowbit(x) (x&(-x))
typedef long long int64;
class BIT {
private:
    vector<int64> delta_1, delta_2;
public:
    BIT(int n) :delta_1(n + 5), delta_2(n + 5) {}
    void add_for_dif(int64 x, int64 k) {
        const int64 i_k = k * x;
        while (x < arr.size()) {
            delta_1[x] += i_k;
            delta_2[x] += k;
            x += lowbit(x);
        }
    }
    void modify(int left, int right, int64 k) {
        add_for_dif(left, k), add_for_dif(right + 1, -k);
    }
    int64 query_for_dif(int64 x) {
        int64 ret = 0;
        int pos = x;
        while (pos) {
            ret += (x + 1) * delta_2[pos] - delta_1[pos];
            pos -= lowbit(pos);
        }
        return ret;
    }
    int64 sum_for_dif(int left, int right) {
        return this->query_for_dif(right) - this->query_for_dif(left - 1);
    }
};

三、珂朵莉树

1. 珂朵莉树原理

• 详情见经典讲解
• 经典例题——珂学题

接下来我用自己的话大概描述一下思路

• 其实珂朵莉树相当于维护了许多小区间，一般初始化状态与数组差不多，维护了\([i,i]\)值为\(0\)的一颗树，但是当我们的区间操作多起来后（或者数据随机时），这种暴力维护方式的复杂度就会大大降低到可以接受的范围内。

核心操作一：split()函数

• 这是珂朵莉树的灵魂操作，该函数用来切开原有区间，并返回要更新的区间迭代器。

核心操作二：assign()函数

• 该函数用于进行区间推平操作，用于将整个区间值变为\(x\)。

自己的板子（不完全版）

typedef long long int64;
class chtholly_node {
public:
	mutable int64 val;
	mutable int l, r;
	chtholly_node(int L, int R, int64 Val) :l(L), r(R), val(Val) {}
	bool operator<(const chtholly_node& x) const{
		return this->l < x.l;
	}
};
class chtholly_tree: public set<chtholly_node> {
public:
	typedef chtholly_node node;
	typedef set<chtholly_node>::iterator iter;
	set<node> s;
	iter split(int pos) {
		/*
			if find a section whose left boundry is equal to pos
			return this section
		*/ 
		iter iter_l = s.lower_bound(node(pos, -1, 0));
		if (iter_l != s.end() and pos == iter_l->l) {
			return iter_l;
		}
		/*
			jump to the section whose left boundry is smaller than pos,
			then process the split procedure, which is modifying the right boundry to (pos-1)
			as simultaneously insert a new section as (pos,iter->r)
		*/
		--iter_l;  
		iter iter_r = s.insert(node(pos, iter_l->r, iter_l->val)).first;
		/*
			insert function return a pair type value as pair<iter,bool>
			bool reflect whether the insert process is successful
		*/
		iter_l->r = pos - 1;
		return iter_r;
	}
	void assign(int left, int right, int64 x) {
		iter iter_r = this->split(right + 1), iter_l = this->split(left);
		/*
			Erase all the nodes in [left,right+1), 
			which means  all the nodes in [left,right]
			* set::erase(iter_l,iter_r):erase elements in [iter_l,iter_r)
		*/
		s.erase(iter_l, iter_r);
		s.insert(node(left, right, x));
	}
	void insert(int left, int right, int64 x) {
		s.insert(node(left, right, x));
	}
	void add(int left, int right, int64 x) {
		iter iter_r = this->split(right + 1), iter_l = this->split(left);
		for (; iter_l != iter_r; ++iter_l) {
			iter_l->val += x;
		}
	}
	int64 query(int left, int right) {
		int64 ret = 0;
		iter iter_r = this->split(right + 1), iter_l = this->split(left);
		for (; iter_l != iter_r; ++iter_l) {
			ret += (iter_l->r - iter_l->l + 1) * iter_l->val;
		}
		return ret;
	}
};

e,g.1 贴海报——经典珂学题

• 蛮裸的题，加一个\(check\)函数即可

int check(int left,int right){
		iter iter_r=this->split(right+1),iter_l=this->split(left);
		int ret=0;
		vector<bool> vis(m+1);
		for(;iter_l!=iter_r;++iter_l){
			if(iter_l->val>0 and !vis[iter_l->val]){
				vis[iter_l->val]=1;
				ret++;
			}
		}
		return ret;
	}
void solve(){
	chtholly_tree tree;
	tree.insert(1,n,0);
	for(int i=1;i<=m;i++){
		int l=read(),r=read();
		tree.assign(l,r,i);
	}
	ans=tree.check(1,n);
	printf("%d",ans);
}
signed main(){
	n=read(),m=read();

	solve();

	return 0;
}

四、ST表

• ST表是用来查询静态区间最大值的数据结构

class logn {
private:
	vector<int64> log;
	int maxn;
public:
	logn(int n) :log(n + 1),maxn(n) {
		pre();
	}
	void pre() {
		log[2] = 1;
		for (int i = 3; i < maxn; i++) {
			log[i] = log[(i >> 1)] + 1;
		}
	}
	int64 operator[](int x) {
		return log[x];
	}

};
void solve() {
	logn pre(n + 1);
	vector<vector<int64>> st(n + 1, vector<int64>(pre[n]+1));
	for (int i = 1; i <= n; i++) {
		st[i][0] = read();
	}
	for (int j = 1; j <= pre[n]; j++) {
		for (int i = 1; i <= n - (1 << j) + 1; i++) {
			st[i][j] = max(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);
		}
	}
	while (m--) {
		int l = read(), r = read();
		int64 k = pre[r - l + 1];
		printf("%lld\n", max(st[l][k], st[r - (1 << k) + 1][k]));
	}

	return;
}

• 别人写的板子

template<typename T, typename Op>
class SparseTable {
public:
    using value_type = T;
    using size_type = unsigned;

private:
    Op op;
    size_type n;
    std::unique_ptr<value_type[]> data;

    static constexpr size_type log2(size_type n) {
        return 31 - __builtin_clz(n);
    }

    static constexpr size_type log(size_type n) {
        return n > 1 ? log2(n - 1) + 1 : n;
    }

    void build() {
        const auto ptr = data.get();
        for (size_type i = 1;(1 << i) < n;++i) {
            const auto pre = ptr + n * (i - 1);
            const auto cur = ptr + n * i;
            const size_type d = 1 << (i - 1);
            const size_type m = n - (1 << i);
            for (size_type j = 0;j <= m;++j)
                cur[j] = op(pre[j], pre[j + d]);
        }
    }

public:
    template<typename It>
    SparseTable(It s, size_type n, const Op& op = Op{})
        : op(op), n(n), data(std::make_unique<value_type[]>(n * log(n))) {
        const auto ptr = data.get();
        std::copy_n(s, n, ptr);
        build();
    }

    template<typename S>
    SparseTable(const S& s, const Op& op = Op{})
        : SparseTable(std::data(s), std::size(s), op) {}
    
    value_type query(size_type l, size_type r, const value_type& unitary = value_type{}) const {
        if (r <= l) return unitary;
        const size_type h = log(r - l) - 1;
        const auto row = data.get() + n * h;
        return op(row[l], row[r - (1 << h)]);
    }
};

template<typename It, typename Op>
SparseTable(It, std::size_t, const Op&)
    -> SparseTable<typename std::iterator_traits<It>::value_type, Op>;

template<typename S, typename Op>
SparseTable(const S& s, const Op& op)
-> SparseTable<typename std::iterator_traits<decltype(std::begin(s))>::value_type, Op>;

五、对顶堆

• 常用于维护、查询第 \(k\) 大元素（或找到中位数）。
• 由一个大根堆和一个小根堆组成，大根堆维护 \(rank\in [1,k]\) 的元素，堆顶为当中最大（即第 \(k\) 大元素）。

找中位数

• 维护 \(k=\frac{n}{2}\) 的对顶堆即可。

void solve() {
	pq<int, vector<int>, greater<int>> q_2;
	pq<int> q_1;
	int t = read();
	q_1.emplace(t);
	printf("%d\n", t);
	for (int i = 2; i <= n; i++) {
		int tmp=read();
		if (tmp > q_1.top()) {
			q_2.emplace(tmp);
		}
		else {
			q_1.emplace(tmp);
		}
		while (abs(q_1.size() - q_2.size() > 1)) {
			if (q_1.size() > q_2.size()) {
				q_2.emplace(q_1.top());
				q_1.pop();
			}
			else {
				q_1.emplace(q_2.top());
				q_2.pop();
			}
		}
		if (i & 1) {
			printf("%d\n", q_1.size() > q_2.size() ? q_1.top() : q_2.top());
		}
	}

	return;
}