杂项记录

一、格雷码

手动构造方法

\(k\)位格雷码可以由以下方法构造：
1.翻转最低位得到下一个格雷码（e.g. 000->001）
2.将最右位的1的左边的位翻转得到下一个格雷码（e.g. 001->011）
交替上述策略\(2^k-1\)次。

计算方法

观察\(G(n)\)与n的二进制，可以发现如果\(G(n)\)的\(i\)位是1，那么n的\(i\)位是1，\(i+1\)位是0||第\(i\)位是0，\(i+1\)位是1.
用代码实现：

int g(int n) {return n^(n>>1);}

证明

 考虑n和n+1的区别，n+1相当于是将n二进制末尾的k个连续的1变成0，k+1位由0变成1。

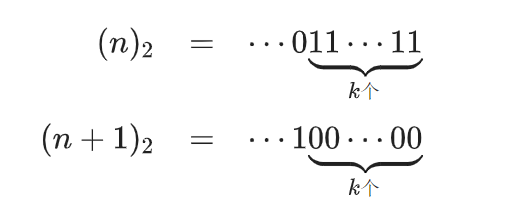
 而经过上文变化后，n和n+1的后k位都会变成10000...0(k个)，而k+1位不同。

代码

class Solution {
public:
    vector<int> grayCode(int n) {
        vector<int> num;
        for(int i=0;i<=((1<<n)-1);i++){
            num.push_back(i^(i>>1));
        }
        return num;
    }
};

格雷码逆变换

二、第二类斯特林数

\(S(n,k)\)，表示将n个两两不同的元素，划分为k个互不区分的非空子集的方案数（即将n个不同小球放在k个相同盒子里）。
递推式为：\(S(i,j)=S(i-1,j)*j+S(i-1,j-1)\)
考虑将\(i-1\)个球放入\(j\)个盒子，可以分为两种情况：

1. 将插入的球放在\(j\)个已经放好的盒子里，有\(j\)种放法。
2. 先将\(i-1\)个球放在\(j-1\)个盒子里，在将插入的球放在剩下的盒子里，由于盒子是不同的，所以加上\(S(i-1,j-1)\)即可。

代码实现

int s[10][10];
int main(){
	int n,m;
	cin>>n>>m;
	s[0][1]=1;
	for(int i=0;i<=n;i++){     
		//从放0个球开始算,最后算到n个球放到n个盒子为止
		for(int j=1;j<=i;j++){
			s[i][j]=s[i-1][j]*j+s[i-1][j-1];
		}
	}
	cout<<s[n][m];
	//cout<<s[n][m]*factory[m];   如果盒子不同要乘上m！
	
	return 0;
}

公式计算

FFT卷积（我不会qwq）

int main() {
  scanf("%d", &n);
  fact[0] = 1;
  for (int i = 1; i <= n; ++i) fact[i] = (ll)fact[i - 1] * i % mod;
  exgcd(fact[n], mod, ifact[n], ifact[0]),
      ifact[n] = (ifact[n] % mod + mod) % mod;
  for (int i = n - 1; i >= 0; --i) ifact[i] = (ll)ifact[i + 1] * (i + 1) % mod;
  poly f(n + 1), g(n + 1);
  for (int i = 0; i <= n; ++i)
    g[i] = (i & 1 ? mod - 1ll : 1ll) * ifact[i] % mod,
    f[i] = (ll)qpow(i, n) * ifact[i] % mod;
  f *= g, f.resize(n + 1);
  for (int i = 0; i <= n; ++i) printf("%d ", f[i]);
  return 0;
}

三、偏序关系

1. 定义与性质

偏序关系 ：对于集\(a\)上的二元关系\(r\)，若具有性质：

• 反自反性：\(\forall x \in a((x, x) \notin r)\)，即\(a\)中元素不能与自身具有关系\(r\)；
• 可递性：\(\forall x,y,z \in a((x,y) \in r \wedge(y,z) \in r \rightarrow(x,y) \in r)\)，即对于\(a\)中三个元素\(x,y,z\)，如果\(x,y\)具有关系\(r\)，且\(y,z\)具有关系\(r\)，则\(x,y\)具有关系\(r\)；
  则\(r\)称为集\(a\)上的偏序关系(partial order relation)
  偏序集：带有偏序\(r\)的集称为\(r\)的偏序集
  偏序结构：偏序集\(a\)与其上的偏序\(r\)共同形成偏序结构，记作\(\langle a,r \rangle\)。
  为了方便起见，\((x,y)\in r\)常简写成\(xry\)。

2.相关算法

一维偏序（逆序对）：对于给定的数列\(\{a_{i}\}\)，求出满足\(i<j\)且\(a_{i}>a_{j}\)的数目。
解决方法：

• 树状数组：对与一个要处理的数列\(\{a_{i}\}\)，逆序取出\(a_{i}\)，每次先进行ans+=query(a_{i})查询该数前缀和，再进行tree[a_{i}]++操作。复杂度为\(O(nlogn)\)
• 归并排序：太经典了，不是重点

二维偏序：对于给定\(n\)个点的坐标，求出满足\(x_{i}<x_{j}\)且\(y_{i}<y_{j}\)的二元组\((i,j)\)的数目。
解决方法：以\(x\)或\(y\)为关键字进行排序，然后转化为一维偏序问题即可。