最小生成树——稠密图——prim算法

#include <algorithm>
#include <cstring>
#include <cstdio>
#include <iostream>

using namespace std;

const int N = 505, INF = 0x3f3f3f3f;
int n, m;
int g[N][N]; //邻接矩阵，储存所有边
int dist[N]; //储存其他点到当前最小生成树这个集合的距离
bool st[N];  //储存每个点是否在最小生成树中

int prim()
{
    int ans = 0;
    for (int i = 0; i < n; i ++ )
    {
        int t = -1;
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[j] < dist[t])) t = j;

        st[t] =true;

        if (i && dist[t] == INF) return INF;//如果是第一次更新那么dist数组就全都为0x3f3f3f3f,此时只是将1号点加进集合中
        if (i) ans += dist[t];

        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], g[t][j]);
    }

    return ans;
}

int main()
{
    memset(g, 0x3f, sizeof g);
    memset(dist, 0x3f,sizeof dist);
    cin >> n >> m;

    while (m -- )
    {
        int a, b, c;
        cin >> a >> b >> c;
        g[a][b] = g[b][a] = min(g[a][b], c);
    }

    int ans = prim();

    if (ans == INF) puts("impossible");
    else cout << ans << endl;
    return 0;
}

dist数组储存的是图中所有的点到最小生成树的距离，由于一个点只能被加入一次那么加入之后这个点到生成树中的距离就可以看成是无穷大，而其他不在生成树中的距离就是生成树中的个点到不在生成树中的点的距离即

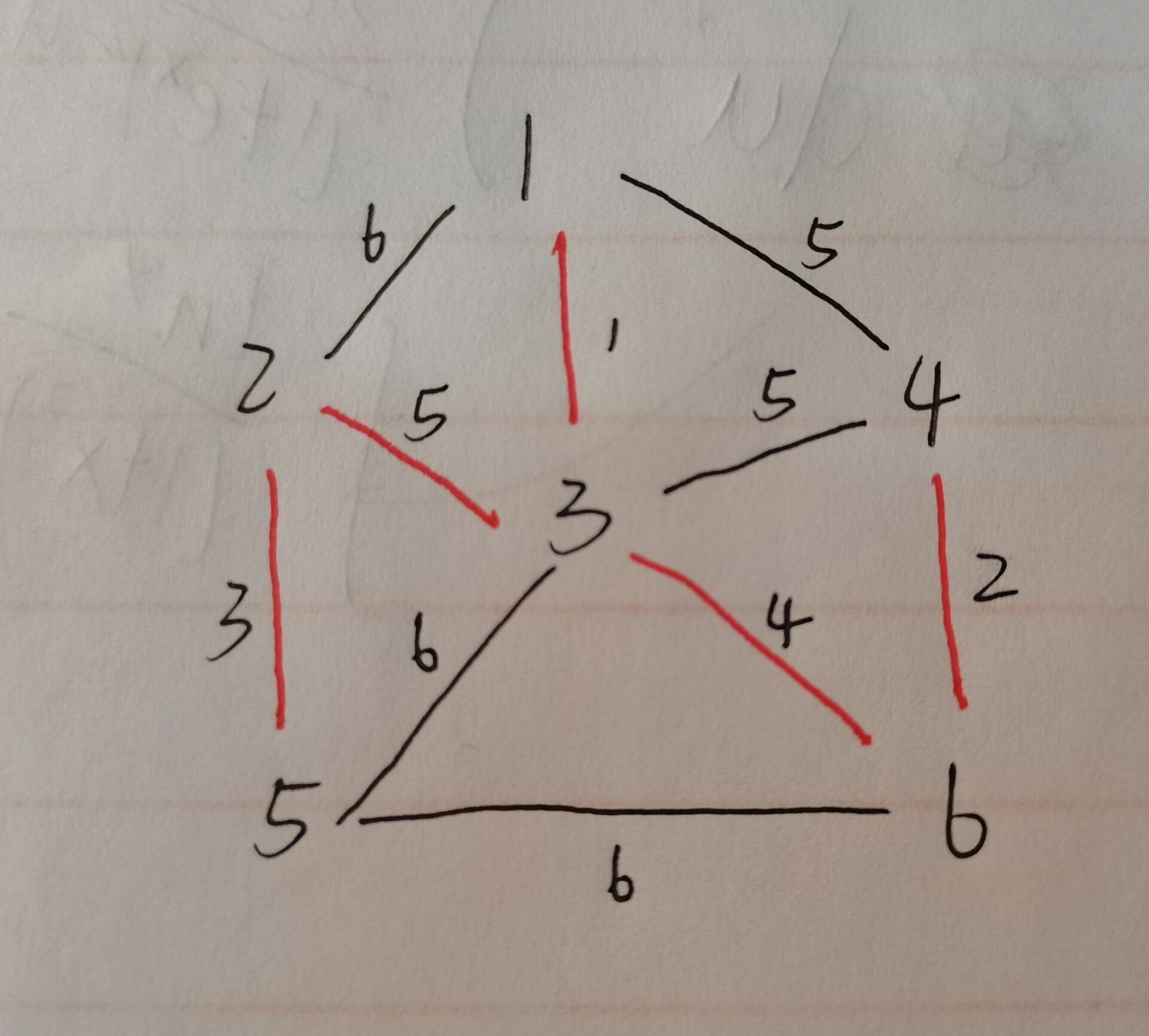
 此时dist数组的变化即为

Max 6   1   5   Max Max 
1   5   1   5   6   4 
1   5   1   2   6   4 
1   5   1   2   6   2 
1   5   1   2   3   2 
1   3   1   2   3   2