随机过程预备知识

一、一维随机变量

1、随机变量

定义：

随机变量的取值随试验的结果而定，在试验之前不能预知它取什么值，且它的取值有一定的概率，这些性质显示了随机变量与普通函数有着本质的差异。随机变量的引人，使我们能用随机变量来描述各种随机现象，并能利用数学分析的方法对随机试验的结果进行深入广泛的研究和讨论。

2、离散型随机变量

有些随机变量，它全部可能取到的值是有限个或可列无限多个，这种随机变量称为离散型随机变量。

例如：某城市120急救电话台一晚上收到的呼唤次数是一个离散型随机变量。

下面介绍三种重要的离散型随机变量：

（1）、两点分布

例如：对新生儿的性别（男or女）进行登记

（2）、二项分布

这里“重复”是指在每次试验中P(A)=p保持不变；“独立”是指各次试验的结果互不影响

例如：

竖(n k)记C^k_n

（3）、泊松分布

例如：一本书一页中的印刷错误数

3、分布函数

4、连续型随机变量

下面介绍三种重要的连续型随机变量：

（1）、均匀分布

（2）、指数分布

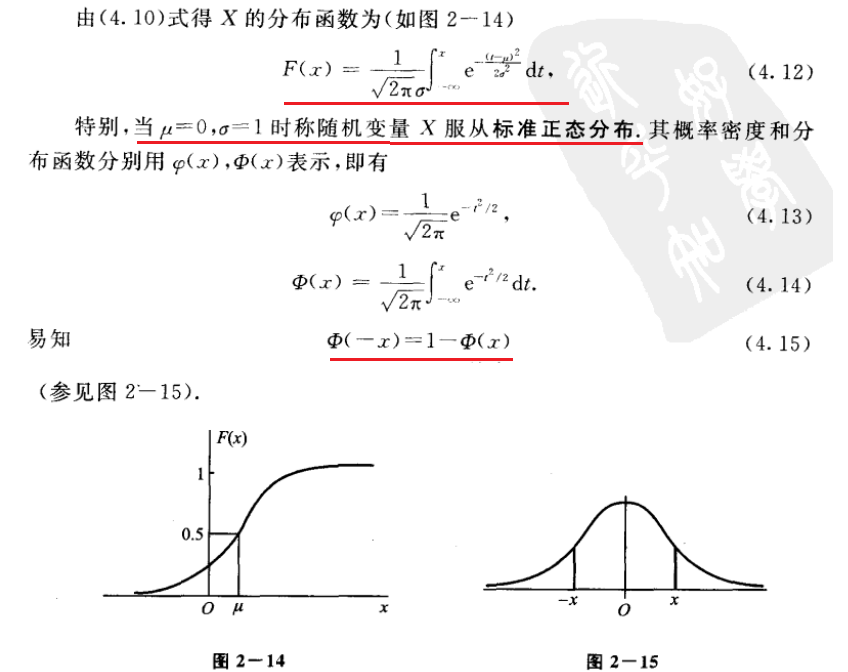
（3）、正态分布

5、随机变量的函数的分布

在实际中，我们常对某些随机变量的函数更感兴趣。例如，在一些试验中，所关心的随机变量往往不能由直接测量得到，而它却是某个能直接测量的随机变量的函数。比如我们能测量圆轴截面的直径d，而关心的却是截面面积A=1/4r(d^2)，这里随机变量A是随机变量d的函数。

二、二维随机变量

1、二维随机变量

定义

联合分布函数

定义

性质

联合分布律

联合概率密度

2、边缘分布

3、条件分布

条件分布律

条件概率密度

4、相互独立的随机变量

非重点

5、两个随机变量的函数的分布

（1）、Z=X+Y的分布

（2）、Z=Y/X的分布、Z=XY的分布

（3）、M=max{X,Y}及N=min{X,Y}的分布

三、随机变量的数字特征

1、数学期望

数学期望(mean)是试验中每次可能结果的概率乘以其结果的总和。它反映随机变量平均取值的大小。

离散型数学期望

连续型数学期望

随机变量函数的数学期望

二维随机变量函数的数学期望

性质

2、方差

定义

计算

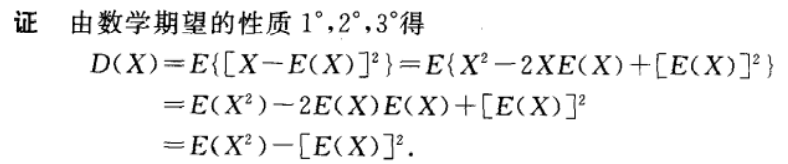
性质

切比雪夫不等式

3、协方差及相关系数

定义

性质

相关系数定理