读书笔记:OpenPBR 规范(4)
3.3 薄膜彩虹色
薄膜彩虹色是指当一层厚度与光波波长相当的薄电介质膜覆盖在材料表面时,由于薄膜内各种电磁反射模式之间的波干涉效应,在反射光中产生类似彩虹的颜色条纹的现象。为模拟此现象,假定在基底(无论是金属还是电介质)上方存在这样一层薄膜,其参数仅由以下几项定义:
- thin_film_weight(薄膜权重):薄膜的覆盖度(存在性)权重。
- thin_film_thickness(薄膜厚度):薄膜的厚度,以微米($ \mu $m)为单位,主要影响颜色条纹的间距。
- thin_film_ior(薄膜折射率):薄膜的折射率,主要影响颜色条纹的色调。
覆盖权重的作用是在存在薄膜和不存在薄膜的 BSDF 之间进行混合,从而允许用户在不改变颜色条纹的形状和饱和度的前提下,调整该效果的强度。
目前推荐的薄膜模型是 Belcour 和 Barla 提出的模型 [Belcour2017]。薄膜反射产生的条纹图案的形状和颜色会受到薄膜上下相邻介质的复折射率的影响(如 Belcour 和 Barla 所述)。通常情况下,薄膜下方是金属和电介质的统计混合介质,而薄膜上方是涂层和环境介质(绒毛层与上方介质折射率匹配)。图 10 展示了取决于薄膜和涂层是否存在而产生的八种可能的不同结构,每种结构都会因界面处不同的折射率而导致不同的菲涅耳效应。
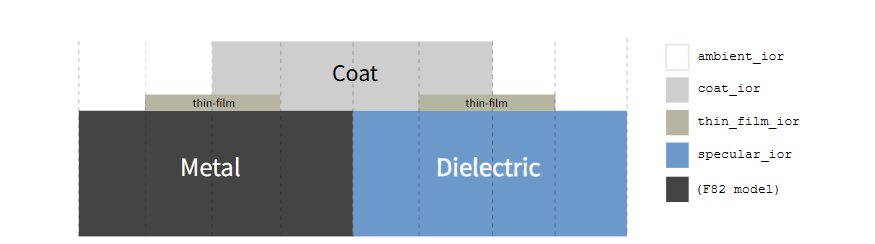
图10:所有8种可能的IOR配置示意图,包括涉及薄膜的那些配置。
原则上,实现应该正确处理所有这些物理配置,尽管精确效果的建模取决于具体实现。在实践中,这种波动光学效应最容易直接并入金属和介质基底层微表面BSDF的菲涅耳因子中。(因此,该效应不是通过将显式薄膜纳入模型来表示的)。
请注意,在介质基底的情况下,薄膜还应在透射波瓣中产生彩色条纹。这在渲染肥皂泡等情况下很重要(参见[Belcour2017])。
在金属基底的情况下,物理特性有些模糊,因为如金属部分所述,金属的菲涅耳因子是根据基于Schlick的"F82-tint"参数化定义的,该参数化未指定底层物理复折射率。我们建议采用某种合理的近似方法,将菲涅耳因子映射到最佳匹配的有效复折射率,例如[Gulbrandsen2014]中描述的方法。

图11:薄膜厚度在0、0.5、1.0微米范围内的变化
3.4 涂层
涂层是一种介电质层,能够透射光线而不发生散射,但可能存在吸收现象。这旨在模拟具有彩色清漆或漆面涂层物体的外观:
界面BSDF f_coat 是一个基于coat_roughness和coat_roughness_anisotropy参数化的GGX微面元介电质模型(参见微面元模型部分)。该介电质层的折射率coat_ior与基础介电质层不同,如下所述。同时假定存在一个纯吸收介质 V_coat。
涂层应用于基础基底之上,覆盖权重 S_coat = coat_weight 如下:

介质 V_coat 的吸收由coat_color参数化,该参数被设定为表示涂层在法向入射时的透射率平方(即 T²_coat = coat_color)。因此,在法向入射时,由于涂层中的吸收沿入射和出射光线路径,观察到的底层基底色调颜色大致由coat_color给出(注意涂层本身的镜面反射不会被着色)。
涂层介质 V_coat 的折射率 S_coat = IOR 将改变涂层顶部界面以及底层金属或介电质的菲涅耳因子。如果存在分数覆盖 S_coat,则基础介电质或金属的周围折射率会在表面统计变化,这取决于涂层是否局部存在(绒毛层可假定具有环境折射率 S_coat)。因此,镜面折射率 S_coat 与周围介质之间的比率可以合理地近似为:
该比率随后决定了镜面菲涅耳因子,如公式modulated_ior所示。(请注意,如涂层全反射部分所述,在模拟涂层内部光线折射时,可能需要对镜面菲涅耳因子的评估进行进一步修改)。

图12:涂层增加了次级高光反射和可选的吸收色调
在完整的光线传输过程中,由于涂层内部的多次内部反射,观察到的涂层基底颜色会变暗并饱和度增加。这些反射使光线多次照射底层材料并经历更多吸收,同时观察到的涂层颜色色调也会随着入射角的变化而变暗,这是由于在涂层介质中光路长度的改变所致。此外,粗糙涂层的存在会增加底层基底BSDF波瓣的表观粗糙度。
我们假设在真实外观中,所有这些物理效应都已被考虑在内。在以下小节中,我们将详细说明实现这些效应的建议方案。
3.4.1 粗糙化
如果涂层粗糙,底层基底(金属和介电质)的微表面BSDF波瓣也会被有效地粗糙化。如果光线传输未另行考虑此效应,可以通过直接改变基底BSDF的法线分布函数(NDF)来合理近似。
我们推荐的公式是通过将每个微表面波瓣的NDF识别为大致对应于斜率空间中的高斯分布,其方差由αt2+αb2=r4给出(使用微表面模型部分的符号)。将粗糙化效应建模为这些高斯NDF的卷积(由于反射两次穿过涂层边界,因此涂层方差被重复计算),基底修正后的粗糙度rB′(考虑涂层的存在权重\(C=coat\_{weight}\))由下式给出:
其中\(r_{\mathrm{B}}=\text{specular\_roughness}\)(基底镜面粗糙度),\(r_{\mathrm{C}}=\text{coat\_roughness}\)(涂层粗糙度)。
3.4.2 变暗效应
图13展示了具有木纹纹理的纹理化漫反射基底和光滑清漆在不同折射率(IOR)下,在法向入射时外观的物理正确变化,显示了基底的变暗效应——这是由于涂层内部的反射造成的——该效应随着IOR的增加而增强。

然而,这种暗化效果在艺术创作中可能并非总是期望的,因为在某些应用场景中,希望涂层后的观察颜色能够"匹配"输入的基础颜色(其精确定义见下文公式62)。为此,我们引入了 coat_darkening 参数 $ \delta $ 来实现这一需求。默认情况下 $ \delta=1 $,此时会正常产生由内部反射引起的物理正确的暗化效果。而当 $ \delta=0 $ 时,基础反照率会被均匀提升,提升量恰好足以抵消暗化效应。该提升因子会随着 $ \delta\to 1 $ 而线性减小至1。
我们所说的"抵消暗化"是指在法线入射方向观察时,涂层基底的反照率 $ E_{c} $ 等于"未暗化"的反照率:
其中 $ E_{b} $ 是法线入射下的基础反照率。这个定义直接解释了涂层基底观察颜色匹配未涂层基底的要求,同时考虑了涂层菲涅耳效应的存在。由于内部反射导致的物理暗化效应,通常需要将基础BSDF通过某个补偿性的均匀"提升"因子 $ B_{0} $ 进行增强,才能使涂层基底达到此未暗化反照率。$ \delta=\text{coat_darkening} $ 的效果则定义为对应用提升因子的以下调制:
虽然这在物理层面定义了行为,但在实践中,实现方需要为涂层暗化效应开发某种特定的近似方法。尽管这可能依赖于具体实现,但我们在此提出一种合理简单、高效的方案,它能捕捉到核心行为。
可以证明,在具有(恒定)反照率 $ E_{b} $ 的朗伯基底和完美光滑的电介质清漆涂层的情况下——即所谓的界面朗伯模型([Elias2001], [d'Eon2021])——涂层基底的确切方向性反照率具有类似反照率缩放的形式(其中 $ \eta_{c} $ 是涂层折射率与环境折射率的比值,F 是相应的涂层菲涅耳因子):
其中 $ \Delta(E_{b},\eta_{c}) $ 是一个暗化因子,由下式给出:
因此,我们可以将所需的提升因子近似为其倒数,即 $ B_{0}\approx\Delta^{-1} $。注意,当 $ E_{b}\to 1 $ 时,暗化因子 $ \Delta\to 1 $,这是符合物理规律的,因为如果基底反射了所有入射能量(在清漆涂层情况下),则没有能量损失。如果基础反照率 $ E_{b} $ 被提升了 $ B(\delta) $ 倍,那么显然在 $ \delta=0 $ 时,暗化因子被抵消,公式62的要求得以满足。
这里的 $ K\in[0,1] $ 是内部漫反射系数,表示离开基底的能量中因涂层内部反射而返回基底的比例。K 值越高,内部反射越多,从而导致更明显的暗化和饱和度增加。在朗伯基底的情况下(这应该是粗糙金属、电介质或漫反射情况的合理近似),$ K=K_{r} $,其中,对于相对涂层折射率 $ \eta_{c} $:
反照率 $ E_{F}(\eta_{c}) $ 是涂层菲涅耳因子的半球(或平均)反照率 $ {}^{10} $。如果基底具有镜面反射(由于光滑的金属或电介质界面),则公式65仍然适用,但内部漫反射系数 K 的适当值应更接近:
这在完美光滑的金属或电介质基底的情况下是精确的。在光滑基底的情况下,暗化效应显著减弱,因为基底的镜面反射不太可能在涂层边界产生全内反射。
因此,我们建议在一般情况下采用公式 65 的暗化因子,但需取:
其中 $ r_{b} $ 是有效基础粗糙度的估计值,该值根据基底金属度 M 在电介质粗糙度 $ r_{d} $ 和金属粗糙度 $ r_{m} $ 之间进行混合:
基础电介质粗糙度 $ r_{d} $ 可以合理地估计为假定的底层基底的高粗糙度与微面元电介质粗糙度 $ r = \text{specular_roughness} $ 的混合,混合权重为由 specular\_weight $ \xi_{s} $ 调制的基础电介质菲涅耳因子(参见公式 25 和公式 26):
而金属粗糙度可取为 $ r_{m}=r $。
给定暗化效应的一般公式 65,一个合理的近似方案是(假设未采用其他补偿方法来近似该效应)将基础 BSDF 乘以经过调制的均匀暗化因子(需考虑存在权重 $ C = \text{coat_weight} $ 和暗化参数 $ \delta = \text{coat_darkening} $):
其中 $ \Delta $ 通过公式 65 计算,其内部漫反射系数(已考虑基础粗糙度)由公式 68 给出。
公式 65 中出现的基础反照率 $ E_{b} $ 表示涂层下方整个基底在法线入射方向的反照率。该反照率可以近似为基底各单独板层在法线入射方向的反照率,根据其混合权重进行混合得到。
3.4.3 视角相关吸收
对于吸收性涂层,由于在涂层介质内的光路长度增加,在掠射角度还会出现额外的暗化和饱和度增加效应。这种效应可以通过在涂层 BRDF 中加入一个因子来模拟:
其中 $ \mu_{i}^{t} $ 是入射光线折射进入涂层后的角度余弦,即:
$ \mu_{o}^{t} $ 的计算方式类似。请注意,在法线入射时,该因子简化为 $ T_{\text{coat}}^{2} \(,我们已将其定义为 `coat_color`。\) {}^{11} $

图14:吸收性涂层在掠射角度下颜色会变得更深且更饱和。
3.4.4 全内反射
在实现带涂层电介质基底的BRDF时,还需提及一个可能引发技术难题的问题。请参见图15,该图示意了一条光线从外部环境介质(折射率 $ n_{a} $)折射进入涂层(折射率 $ n_{c} $),然后再折射进入基底电介质(折射率 $ n_{b} $)的过程:
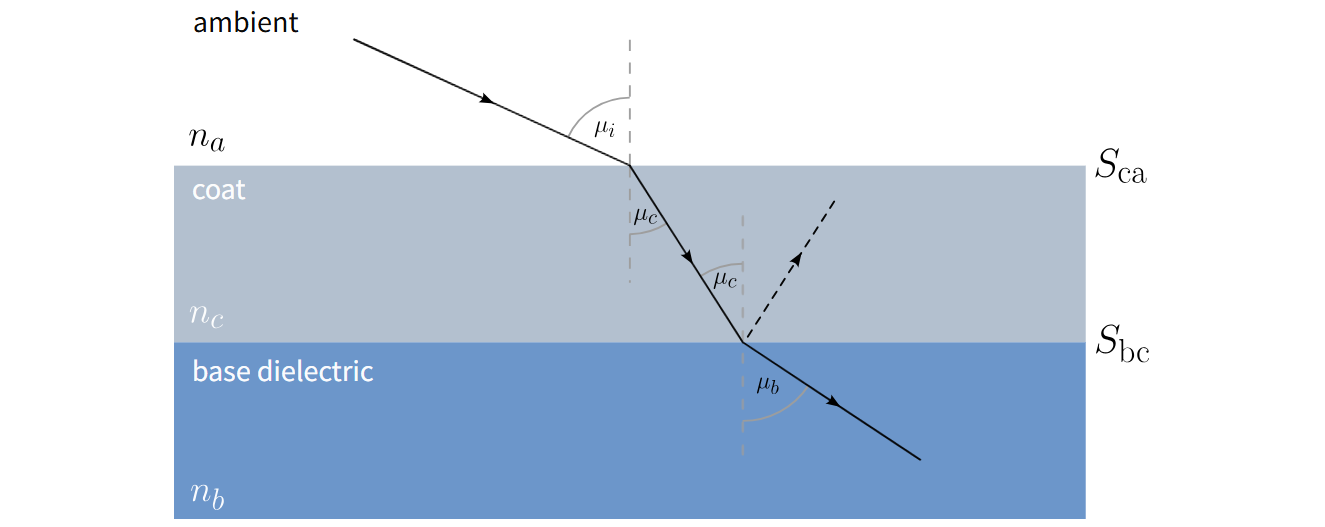
图15:涂层-基底边界处的光线配置。
如果涂层折射率 $ n_{c} $ 大于基底电介质的折射率 $ n_{b} $,那么入射到基底的光线通常会在基底-涂层边界表面 $ S_{bc} $(其折射率比 $ \eta_{bc}=n_{b}/n_{c} $)处发生全内反射。在这种情况下,来自基底的反射(虚线所示)会增强,因为没有光线沿 $ \mu_{b} $ 方向折射进入基底。
然而,如果界面是光滑且平行的,则很容易证明,由于光线在上方涂层-环境介质边界 $ S_{ca} $(其折射率比 $ \eta_{ca}=n_{c}/n_{a} $)处的折射,从外部入射的光线不可能发生此类全内反射。在粗糙界面的一般情况下,全内反射确实可能发生,但随着粗糙度的降低,其发生的可能性会越来越小。因此,如果电介质基底 BSDF 的实现没有考虑入射光线在涂层中的折射,就会产生虚假的全内反射,表现为在接近掠射角时出现明显不正确的明亮"光环"。在将模型简化为作为入射方向函数进行采样的独立波瓣混合的实现中,如何解释这一点并不显而易见。
我们建议采用一种合理的实用近似方法(遵循 [Kutz2021]),即简单地反转涂层-基底边界处的折射率比值,也就是按如下方式替换 $ \eta_{bc} $:
这消除了全内反射,同时合理地保持了镜面反射。然后,为了考虑部分涂层覆盖的情况,在公式 60 中,使用这个修改后的 $ \eta_{bc} $ 来代替 $ n_{b}/n_{c} $ 项。
另一种方法是显式地修改入射到基底的光线的折射角余弦。为简化起见,假设在基底微面元的局部空间中,上覆的涂层微面元具有匹配的微法线,则基底微法线处的角度余弦 $ \mu_{c} $ 由入射角余弦 $ \mu_{i} $ 经如下折射给出:
然后,可以根据涂层的存在权重 $ \mathcal{C} $,将产生的菲涅耳因子近似为在原始入射方向和折射后入射方向处计算的菲涅耳因子的混合:
其中 $ \eta_{\text{ba}}=n_{b}/n_{a} $,然后将这个混合后的菲涅耳因子代入微面元 BRDF(这取代了忽略涂层折射的公式 60 中的菲涅耳计算)。如果 $ \eta_{\text{ca}}<0 $,则可能在 $ S_{\text{ca}} $ 处发生全内反射(即公式 75 中 $ \mu_{c}^{2}\leq 0 $),在这种情况下,可以假设菲涅耳因子 $ F(\mu_{c},\eta_{\text{bc}}) $ 为零。
这两种方案都能产生 plausible 的外观,并消除了虚假的全内反射。更物理正确的方法需要类似于 Weidlich-Wilkie 分层模型 [Weidlich2007] 或《Physically Based Rendering》[Pharr2023] 中描述的分层材质模型的方法,即通过蒙特卡洛模拟显式地对穿过各层的光线散射进行建模。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号