K-D tree 学习笔记
K-D tree 是一种用于处理高维空间信息的数据结构,他的作用就是维护 k 维空间的 n 个点,并且满足平衡树的性质
1. 构建原理
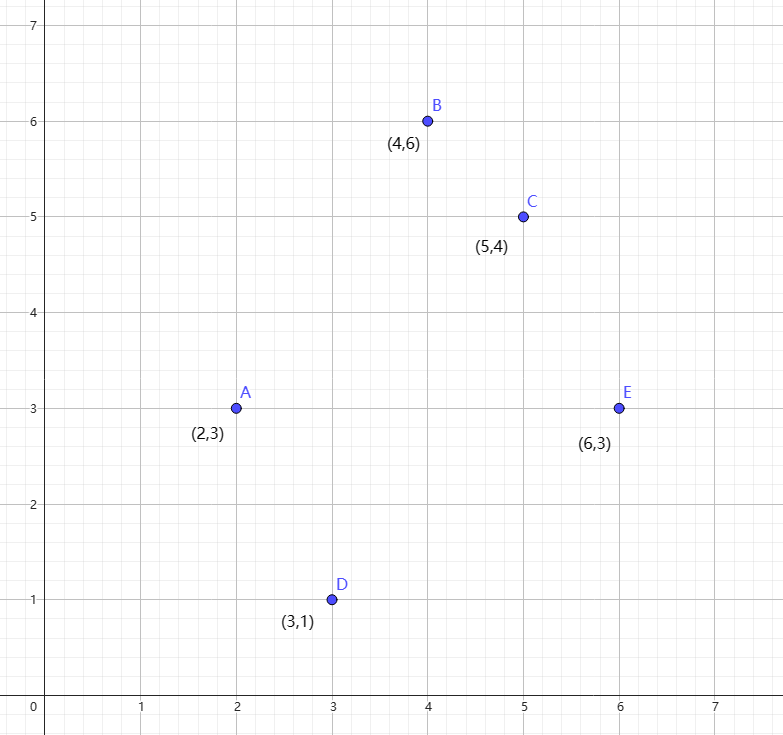
以上面这张图为例,K-D tree 的建立过程是这样的:
首先,以 x 轴为关键字,然后找到中位数,进行划分
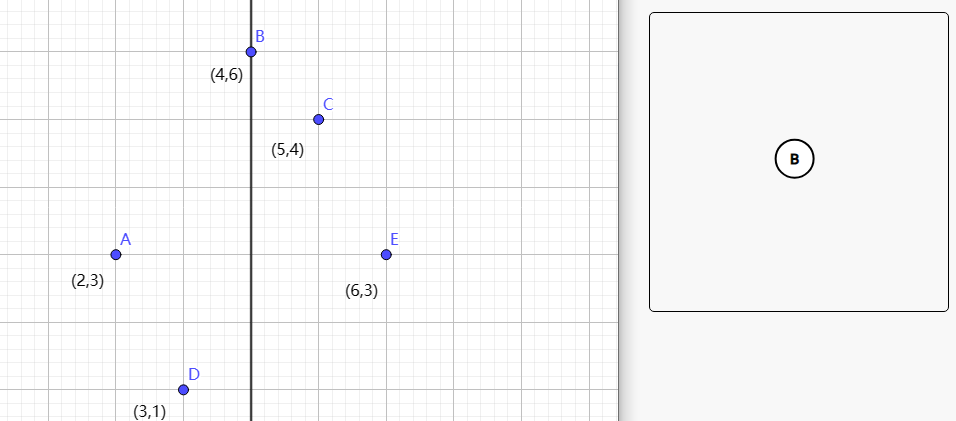
接下来以 y 轴为关键字,分别找到两个块的中位数,此时他们的父亲就是第一次选中的点
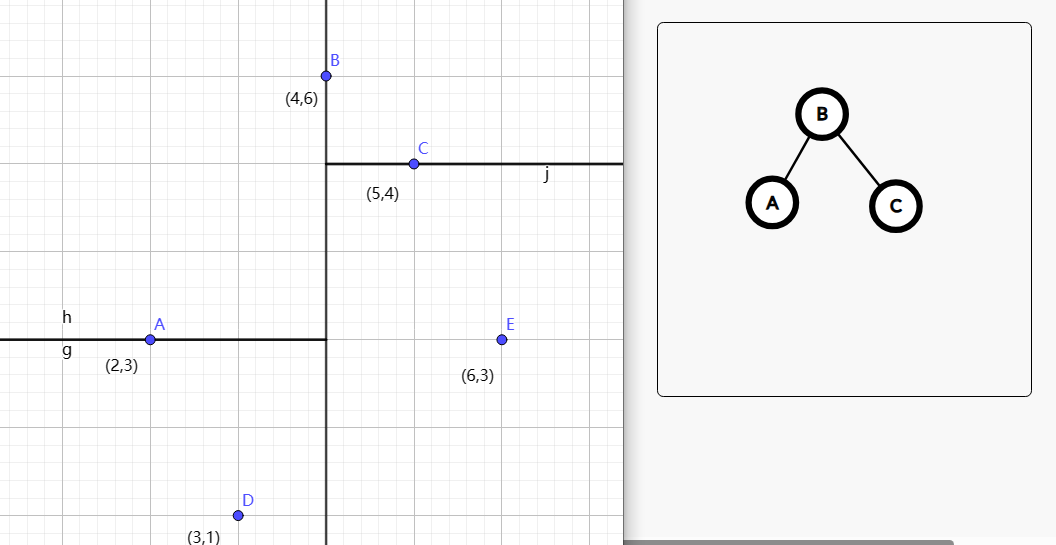
然后以此类推,会得到:
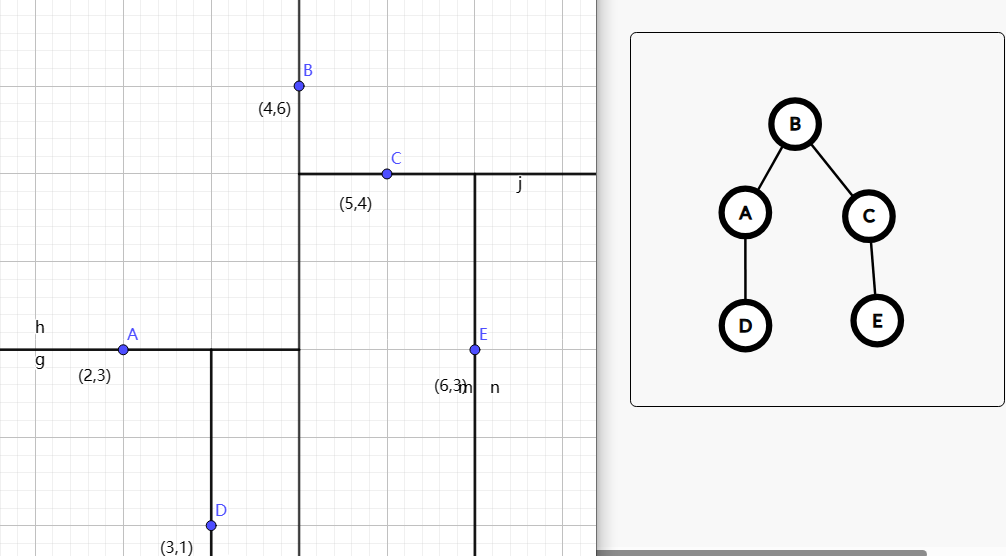
将其推广会得到高维的操作过程:
-
先确定一个维度的中位数,这里的维度尽量轮流选,能够有效防止一维相近,一维差别大的情况
-
将中位数向其父亲连边
-
从当前位置将平面分割,即将当前维度值小于的归到左边,大于的归到右边
-
重复执行如上过程,直到不存在多余的点
性质:
-
同一层关键字相同
-
任意一棵子树都会形成一个矩形,与同一层不会相交
2. 操作
2.1. 建树
最暴力的方法就是跑到每一个点都 sort 一次,但是显然时间复杂度是双 log 的
这里可以考虑快速排序的原理,就是定一个数 mid 将小于它的放到左边,剩下的放到右边
这里有一个函数:nth_element(s+l,s+mid,s+r+1,cmp) 可以让 s[mid] 左边都小于它,右边都大于它
此时从中间分开,就可以不断递归
2.2. 插入/删除
插入可以从根开始 dfs,和每个点对应的维度进行比较划分,然后找到对应位置插入
对于删除,可以采用同样的方法找,然后打上标记即可
2.3. 重构建
观察上面的过程可以发现,如果插入很多,并且碰上 bobo 型 ex 出题人的话,那么就会不平衡
所以可以记录一个数 p 当有一个子树的节点数大于 sum*p 时,对它进行重构
此时可遍历所有点,记录数据,然后build 即可
2.4. 查询
大致分为2种
1. 区域查询
这个和线段树相似,依据性质2,就是如果当前节点子树被完全包含,直接 return,否则继续递归
这里其实不止能查矩形,和一些函数关系式的数量关系组成的域也能查,因为只需要能判断包含关系即可
简单题
为什么叫简单题啊
因为 n 很大,不能树套树,所以 K-D tree 矩形查询
查询具体分为4层判断,如果当前矩形被完全包含,直接加,完全未被包含,退出
当前点被包含,只加点权,最后向存在的儿子递归
点击查看代码
#include<cstdio>
#include<algorithm>
using namespace std;
const double mxs=0.75;
int n;
struct kd_tr{
int ls,rs,sum,val,siz,mx[2],mn[2],d[2];
}tr[500005];
int dim,id[200005],rt,tot;
bool cmp(int a,int b)
{
return tr[a].d[dim]<tr[b].d[dim];
}
void pushup(int p)
{
tr[p].siz=tr[tr[p].ls].siz+tr[tr[p].rs].siz+1;
tr[p].sum=tr[tr[p].ls].sum+tr[tr[p].rs].sum+tr[p].val;
for(int i=0;i<2;i++)
{
tr[p].mx[i]=max(tr[p].d[i],max(tr[tr[p].ls].mx[i],tr[tr[p].rs].mx[i]));
tr[p].mn[i]=min(tr[p].d[i],min(tr[tr[p].ls].mn[i],tr[tr[p].rs].mn[i]));
}
}
void build(int &p,int l,int r,int k)
{
p=0;
if(l>r) return;
int mid=(l+r)>>1;
dim=k;
nth_element(id+l,id+mid+1,id+r+1,cmp);
p=id[mid],tr[p].sum=tr[p].val;
tr[p].mx[0]=tr[p].mn[0]=tr[p].d[0];
tr[p].mx[1]=tr[p].mn[1]=tr[p].d[1];
build(tr[p].ls,l,mid-1,k^1);
build(tr[p].rs,mid+1,r,k^1);
pushup(p);
}
int pos[2],cnt;
void dfs(int p)
{
if(!p) return;
id[++cnt]=p;
dfs(tr[p].ls);
dfs(tr[p].rs);
}
void rebuild(int &p,int k,int v)
{
cnt=0;
id[++cnt]=++tot;
tr[tot].siz=1,tr[tot].val=tr[p].sum=v;
tr[tot].d[0]=pos[0],tr[tot].d[1]=pos[1];
dfs(p);
build(p,1,cnt,k);
}
void insert(int &p,int k,int v)
{
if(!p)
{
// printf("a");
p=++tot;
tr[p].siz=1,tr[p].val=tr[p].sum=v;
tr[p].mx[0]=tr[p].mn[0]=tr[p].d[0]=pos[0];
tr[p].mx[1]=tr[p].mn[1]=tr[p].d[1]=pos[1];
return;
}
if(pos[k]<tr[p].d[k])
{
if(mxs*tr[p].siz<tr[tr[p].ls].siz*1.0) rebuild(p,k,v);
else insert(tr[p].ls,k^1,v);
}
else
{
if(mxs*tr[p].siz<tr[tr[p].rs].siz*1.0) rebuild(p,k,v);
else insert(tr[p].rs,k^1,v);
}
pushup(p);
}
int query(int p,int a,int b,int c,int d)
{
// printf("%d %d %d %d %d\n",p,tr[p].mn[0],tr[p].mn[1],tr[p].mx[0],tr[p].mx[1]);
if(!p) return 0;
if(tr[p].mn[0]>=a&&tr[p].mn[1]>=b&&tr[p].mx[0]<=c&&tr[p].mx[1]<=d)
{
return tr[p].sum;
}
if(tr[p].mn[0]>c||tr[p].mx[0]<a||tr[p].mn[1]>d||tr[p].mx[1]<b) return 0;
int ans=0,l=tr[p].ls,r=tr[p].rs;
if(tr[p].d[0]>=a&&tr[p].d[1]>=b&&tr[p].d[0]<=c&&tr[p].d[1]<=d) ans+=tr[p].val;
if(l) ans+=query(l,a,b,c,d);
if(r) ans+=query(r,a,b,c,d);
return ans;
}
int main()
{
tr[0].mn[0]=tr[0].mn[1]=1e9;
scanf("%d",&n);
int lst=0;
while(1)
{
int opt,a,b,c,d;
scanf("%d",&opt);
if(opt==3) return 0;
if(opt==1)
{
scanf("%d%d%d",&pos[0],&pos[1],&c);
pos[0]^=lst,pos[1]^=lst,c^=lst;
insert(rt,0,c);
}
else
{
scanf("%d%d%d%d",&a,&b,&c,&d);
a^=lst,b^=lst,c^=lst,d^=lst;
// printf("%d",rt);
lst=query(rt,a,b,c,d);
printf("%d\n",lst);
}
}
return 0;
}
2. 邻域查询
一般是解决点对距离的问题,dfs 遍历整棵树,然后用估价函数,按照价值大小搜索
但是会有运气成分,最大的单次查询复杂度为 \(O(n)\)
[SDOI2010] 捉迷藏
https://www.gxyzoj.com/d/gxyznoi/p/P161
就是分别查出每个点到所有点的最大/最小曼哈顿距离即可
点击查看代码
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
int n,id[100005],rt;
struct kd_tr{
int ls,rs,mx[2],mn[2],d[2];
}tr[100005];
int dim;
bool cmp(int a,int b)
{
return tr[a].d[dim]<tr[b].d[dim];
}
void pushup(int p)
{
int l=tr[p].ls,r=tr[p].rs;
for(int i=0;i<2;i++)
{
tr[p].mx[i]=max(tr[p].d[i],max(tr[l].mx[i],tr[r].mx[i]));
tr[p].mn[i]=min(tr[p].d[i],min(tr[l].mn[i],tr[r].mn[i]));
}
}
void build(int &p,int l,int r,int k)
{
p=0;
if(l>r) return;
int mid=(l+r)>>1;
dim=k;
nth_element(id+l,id+mid+1,id+r+1,cmp);
p=id[mid];
tr[p].mx[0]=tr[p].mn[0]=tr[p].d[0];
tr[p].mx[1]=tr[p].mn[1]=tr[p].d[1];
build(tr[p].ls,l,mid-1,k^1);
build(tr[p].rs,mid+1,r,k^1);
pushup(p);
}
int ans_max,ans_min;
int get(int x,int now)
{
return abs(tr[now].d[0]-tr[x].d[0])+abs(tr[now].d[1]-tr[x].d[1]);
}
int get_min(int x,int now)
{
if(!x) return 2e9;
return max(tr[now].d[0]-tr[x].mx[0],0)+max(tr[x].mn[0]-tr[now].d[0],0)+max(tr[now].d[1]-tr[x].mx[1],0)+max(tr[x].mn[1]-tr[now].d[1],0);
}
int get_max(int x,int now)
{
if(!x) return 0;
return max(tr[now].d[0]-tr[x].mn[0],tr[x].mx[0]-tr[now].d[0])+max(tr[now].d[1]-tr[x].mn[1],tr[x].mx[1]-tr[now].d[1]);
}
void query_min(int p,int now)
{
if(!p) return;
if(p!=now) ans_min=min(ans_min,get(p,now));
int vl=get_min(tr[p].ls,now),vr=get_min(tr[p].rs,now);
if(vl<vr)
{
if(ans_min>vl) query_min(tr[p].ls,now);
if(ans_min>vr) query_min(tr[p].rs,now);
}
else
{
if(ans_min>vr) query_min(tr[p].rs,now);
if(ans_min>vl) query_min(tr[p].ls,now);
}
}
void query_max(int p,int now)
{
if(!p) return;
if(p!=now) ans_max=max(ans_max,get(p,now));
int vl=get_max(tr[p].ls,now),vr=get_max(tr[p].rs,now);
if(vl>vr)
{
if(ans_max<vl) query_max(tr[p].ls,now);
if(ans_max<vr) query_max(tr[p].rs,now);
}
else
{
if(ans_max<vr) query_max(tr[p].rs,now);
if(ans_max<vl) query_max(tr[p].ls,now);
}
}
int main()
{
tr[0].mn[0]=tr[0].mn[1]=1e9;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
id[i]=i;
scanf("%d%d",&tr[i].d[0],&tr[i].d[1]);
}
build(rt,1,n,0);
int ans=2e9;
// printf("1");
for(int i=1;i<=n;i++)
{
ans_min=2e9,ans_max=0;
query_min(rt,i),query_max(rt,i);
ans=min(ans,ans_max-ans_min);
// printf("%d %d\n",ans_min,ans_max);
}
printf("%d",ans);
return 0;
}
3. 例题
巧克力王国
https://www.gxyzoj.com/d/gxyznoi/p/P162
看到两个限制条件,应当是 2-D tree,将两者的含量当坐标,放在平面直角坐标系上考虑
这个显然就是一条与 x 轴交于 \((\frac{c}{a},0)\),与 y 轴交于 \((\frac{c}{b},0)\) 的直线下方的权值之和
此时,直接求和即可
JZPFAR
https://www.gxyzoj.com/d/gxyznoi/p/P163
用小根堆存储即可,每次和根进行比较判断能否加入
崂山白花蛇草水
https://www.gxyzoj.com/d/gxyznoi/p/P167
表面上是用优先队列维护前 k 个,但是 k 的范围很大,无法统计
考虑什么能够做到修改和第 k 大查询,考虑权值线段树上二分
在每个节点建立一棵 2-D tree,此时,就可以求出值域在 \([l,r]\) 之间的数的个数
这里因为是不断插入更新,所以要重构建
点击查看代码
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1e5+5,inf=1e9;
const double mxs=0.63;
int n,q,ls[N*8],rs[N*8],rt[N*8],idx,tot;
int pos[2],id[N*2],dim,root;
struct kd_tr{
int ls,rs,siz,d[2],mn[2],mx[2];
}tr[N*35];
bool cmp(int a,int b)
{
return tr[a].d[dim]<tr[b].d[dim];
}
void pushup(int p)
{
int l=tr[p].ls,r=tr[p].rs;
tr[p].siz=tr[l].siz+tr[r].siz+1;
for(int i=0;i<2;i++)
{
tr[p].mn[i]=min(tr[p].d[i],min(tr[l].mn[i],tr[r].mn[i]));
tr[p].mx[i]=max(tr[p].d[i],max(tr[l].mx[i],tr[r].mx[i]));
}
}
void build(int &p,int l,int r,int k)
{
p=0;
if(l>r) return;
int mid=(l+r)>>1;
dim=k;
nth_element(id+l,id+mid+1,id+r+1,cmp);
p=id[mid],tr[p].siz=1;
tr[p].mn[0]=tr[p].mx[0]=tr[p].d[0];
tr[p].mn[1]=tr[p].mx[1]=tr[p].d[1];
build(tr[p].ls,l,mid-1,k^1);
build(tr[p].rs,mid+1,r,k^1);
pushup(p);
}
int cnt,tim;
void dfs(int p)
{
if(!p) return;
id[++cnt]=p;
dfs(tr[p].ls);
dfs(tr[p].rs);
}
void rebuild(int &p,int k)
{
cnt=0,tim++;
id[++cnt]=++tot;
tr[tot].siz=1;
tr[tot].d[0]=pos[0],tr[tot].d[1]=pos[1];
dfs(p);
build(p,1,cnt,k);
}
void insert(int &p,int k)
{
if(!p)
{
p=++tot;
tr[p].siz=1;
tr[p].mn[0]=tr[p].mx[0]=tr[p].d[0]=pos[0];
tr[p].mn[1]=tr[p].mx[1]=tr[p].d[1]=pos[1];
return;
}
if(pos[k]<tr[p].d[k])
{
if(tr[p].siz*mxs<tr[tr[p].ls].siz*1.0) rebuild(p,k);
else insert(tr[p].ls,k^1);
}
else
{
if(tr[p].siz*mxs<tr[tr[p].rs].siz*1.0) rebuild(p,k);
else insert(tr[p].rs,k^1);
}
pushup(p);
}
void update(int &p,int l,int r,int x)
{
if(!p) p=++idx;
insert(rt[p],0);
if(l==r) return;
int mid=(l+r)>>1;
if(x<=mid) update(ls[p],l,mid,x);
else update(rs[p],mid+1,r,x);
}
int query(int p,int a,int b,int c,int d)
{
if(!p) return 0;
if(tr[p].mn[0]>=a&&tr[p].mn[1]>=b&&tr[p].mx[0]<=c&&tr[p].mx[1]<=d)
{
return tr[p].siz;
}
if(tr[p].mn[0]>c||tr[p].mx[0]<a||tr[p].mn[1]>d||tr[p].mx[1]<b) return 0;
int ans=0,l=tr[p].ls,r=tr[p].rs;
if(tr[p].d[0]>=a&&tr[p].d[1]>=b&&tr[p].d[0]<=c&&tr[p].d[1]<=d) ans++;
if(l) ans+=query(l,a,b,c,d);
if(r) ans+=query(r,a,b,c,d);
return ans;
}
int getans(int p,int l,int r,int a,int b,int c,int d,int k)
{
if(l==r) return l;
// if(!p||l>r) return 0;
int tmp=query(rt[ls[p]],a,b,c,d);
int mid=(l+r)>>1;
if(tmp>=k) return getans(ls[p],l,mid,a,b,c,d,k);
else return getans(rs[p],mid+1,r,a,b,c,d,k-tmp);
}
int main()
{
tr[0].mn[0]=tr[0].mn[1]=1e8;
scanf("%d%d",&n,&q);
int lst=0;
while(q--)
{
int opt,x,y,a,b,k;
scanf("%d%d%d%d",&opt,&x,&y,&a);
x^=lst,y^=lst,a^=lst;
if(opt==1)
{
pos[0]=x,pos[1]=y;
update(root,1,inf,a);
}
else
{
scanf("%d%d",&b,&k);
b^=lst,k^=lst;
// printf("%d\n",query(rt[1],x,y,a,b));
int tmp=query(rt[root],x,y,a,b);
if(tmp<k)
{
lst=0;
printf("NAIVE!ORZzyz.\n");
}
else
{
lst=getans(root,1,inf,x,y,a,b,tmp-k+1);
printf("%d\n",lst);
}
}
// printf("%d %d %d\n",tim,cnt,query(rt[1],3769,2510,6455,3216));
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号