第二次作业——个人项目实战之随机数独生成
第二次作业——个人项目实战之随机数独生成
遇到的困难及解决方法
- 解题思路以及中间编程过程描述以及相关代码
在刚刚看到这个题目的时候,第一印象是觉得很难,因为数独在我看来就是一个非常神奇的东西,不是一般的人能破解和构造的。
- 而我在解这个题目时的第一个想法就是:从数组第一个数按照开始往下遍历,并利用一个函数IsSuitable(int row, int col)判断该数在该位置是否合适,IsSuitable的具体实现就是去满足数独的3个规则,满足1-9数字在行和列以及所在九宫格的不重复性,以此寻找可能的解法。但是第一次我便碰壁了,因为我没有考虑的一种情况,天真的我想当然的认为只要遍历一次便能生成整个数独,没有想到一个位置可能1-9这9个数字都不满足的情况,这个时候便需要回溯,尝试修改前一个位置的值去满足这个位置的需求。这便要利用到递归函数和随机函数了。第一种想法可以满足极大的随机性,构造的数独矩阵可以有非常之多,甚至是全部。
- 但是由于一遍一遍的回溯速度可能会非常的慢,因此我又萌生了第二种想法(参考博客请戳),这里我们首先将9X9矩阵按顺序编号为9个3X3矩阵,然后以中间的矩阵为中心,利用列变换生成2号和8号矩阵(我们将所有子矩阵按照行优先的顺序从1-9进行编号),再使用行变换生成4号和6号矩阵,最后分别用4号和6号矩阵利用列变换生成1号、7号矩阵和3号9号矩阵。这样就形成了一个合法的数独。这种方法虽然简单,运行效率也高,但是有一个弊端就是生成的矩阵太有规律,而且生成的矩阵种数大不如第一种想法。
- 因此第三种想法算是第二种想法的一种改变,可以在9X9矩阵中先预设一个模板,如下
只要事先使用随机数给a,b,c,d,e,f,g,h,i赋1-9的数字值,然后在填入如图所示模板上即可生成合理的数独,理论上给9个字母赋值有9的阶层种,但由于本次作业i是固定的,因此只有8的阶层种情况,可以看出,这种方法效率很高,但有局限性,即生成的矩阵总数仍有限制。
- 最后第四种想法是这样子的,也是前面矩阵变换法和回溯法的一个变种结合,即首先随机初始化1,5,9号矩阵,因为1,5,9号矩阵本身是不冲突的,不需要再增加任何判断语句,之后再利用回溯法生成剩下的矩阵。随机生成矩阵的代码如下:
void generate1to9(){
for(int k = 0;k < 9;k++){
temp[k]=0;
}//初始化数组
for(int i=0;i<9;i++){
temp[i]=1+rand()%9; //得到随机数(范围在1-9之间)
for(int j=0;j<i;j++) //判断和前面的数是否重复
if(temp[i]==temp[j]) {i--;break;}//如果重复,重新生随机数
}//产生9个随机数
}// 随机产生1-9不重复的数,结果填到temp数组
- 当然还有**其他种方法**,比如先随机成一行或者一列的数据,然后用回溯法去补充剩下的格子,另外可以先手动填充一个9X9矩阵,然后根据列变换或者行变换去构造更多矩阵,但往往只能构造出少数的几十种罢了。初始的数独终盘生成规则 1、按顺序将1~9填入宫格中; 2、检查所在行、列及小九宫格是否存在相同数字 3、若存在相同数字则将数字加1 ,重复第2步 参考自[博客链接](http://www.cnblogs.com/JasonBourn/p/7279164.html) 当然还有其他的生成算法,有待研究。
设计实现过程
本次设计一共实现两种方法,回溯和模板算法,一共有四个函数
void inti();利用generate1to9()初始化
void generate1to9(); 随机产生1-9不重复的数
bool IsSuitable(int row, int col); 判别数填在该位置是否合适
bool generate(int row, int col);回溯递归实现核心算法
void output();输出函数
(其中回溯法仅仅用到后三个,而模板算法则只用前两个以及最后一个即可)
关键代码分析说明
当然,最关键的还是代码了,以上几种思路我都有尝试过实现,但是大同小异,核心还是在于回溯思想的实现,当然纯矩阵变换以及上述提到的模板算法思想可以除外,这两种相对比较容易实现。
最终我采用了直接回溯法+模板算法的思想,以下是的算法相关组件函数的实现:
(注:因为事先生成随机矩阵的随机性大,运气好的话可以减少时间消耗,运气不好的话也会耗费很多不必要的时间,因为你不知道中间是否会卡住而需要向上回溯,而当你回溯到事先生成的矩阵时,又会多出很多判断~~~我尝试了很久,最终还是没有成功实现)bool Gen::generate(int row, int col) {
int nextrow, nextcol;
vector<int> number;
for (int i = 1; i <= 9; i++)
number.push_back(i);//将1-9装入容器
while (!number.empty()) {
int randindex = rand() % number.size(); //随机产生1到(size-1)里的 1 个 数字randindex
number.erase(number.begin() + randindex); //删除索引位置的数据
num[row][col] = number[randindex]; //将数据填在第row行,第col列
if (!IsSu.IsSuitable(row, col)) continue; //如果 randnum不能填在number[row][col]这个位置,则继续循环找一个合适的数
if (row == SIZE - 1 && col == SIZE - 1) {
return true;
} //如果最右下角的空也填上了,返回ture,成功生成数独矩阵
if (col == SIZE - 1) {
nextrow = ++row;
nextcol = 0;
} //如果探索到最后一列,则换行
else {
nextrow = row;
nextcol = ++col;
} //nextrow,nextcol指向下一个空格
bool next = generate(nextrow, nextcol); //递归遍历整个数独矩阵
if (next) return true; //当返回ture时 矩阵成功生成
}
if (number.empty()) {
return false;
} //生成的时候卡住了便回溯上一层
}
[参考自](http://blog.csdn.net/bupt8846/article/details/43503447) 其中一种模板算法如下:#include<iostream>
#include<cstdlib>
#include<cstdio>
#include<ctime>
#include<vector>
#include<fstream>
using namespace std;
int temp[9];
int num[9][9];
void generate1to9() {
for (int k = 0; k < 9; k++) {
temp[k] = 0;
}//初始化数组
for (int i = 0; i<9; i++) {
temp[i] = 1 + rand() % 9; //得到随机数(范围在1-9之间)
for (int j = 0; j<i; j++) //判断和前面的数是否重复
if (temp[i] == temp[j]) { i--; break; } //如果重复,重新产生随机数
}//产生9个随机数
}// 随机产生1-9不重复的数,结果填到temp数组中
char model[9][9] = {
{ 'i','g','h','c','a','b','f','d','e' },{ 'c','a','b','f','d','e','i','g','h' },{ 'f','d','e','i','g','h','c','a','b' },{ 'g','h','i','a','b','c','d','e','f' },{ 'a','b','c','d','e','f','g','h','i' },{ 'd','e','f','g','h','i','a','b','c' },{ 'h','i','g','b','c','a','e','f','d' },
{ 'b','c','a','e','f','d','h','i','g' },{ 'e','f','d','h','i','g','b','c','a' }
};
void init()
{
generate1to9();
for (int i = 0; i<9; i++) {
if (temp[i] == 6) {
temp[i] = temp[8];
temp[8] = 6;
}
}
}
void generator()
{
for (int i = 0; i<9; i++)
{
for (int j = 0; j<9; j++)
{
if (model[i][j] == 'a') num[i][j] = temp[0];
else if (model[i][j] == 'b') num[i][j] = temp[1];
else if (model[i][j] == 'c') num[i][j] = temp[2];
else if (model[i][j] == 'd') num[i][j] = temp[3];
else if (model[i][j] == 'e') num[i][j] = temp[4];
else if (model[i][j] == 'f') num[i][j] = temp[5];
else if (model[i][j] == 'g') num[i][j] = temp[6];
else if (model[i][j] == 'h') num[i][j] = temp[7];
else if (model[i][j] == 'i') num[i][j] = temp[8];
}
}
}
void output()
{
for (int i = 0; i<9; i++)
{
for (int j = 0; j<9; j++)
{
printf(" %d", num[i][j]);
}
printf("\n");
}
}
int main()
{
clock_t start, finish;
double totaltime;
start = clock();
int n;
printf("请输入您要生成的数独矩阵个数:\n");
int CharJduge = scanf_s("%d", &n);
for (int i = 0; i<n; i++)
{
init();
generator();
output();
printf("\n");
}
finish = clock();
totaltime = (double)(finish - start) / CLOCKS_PER_SEC;
cout << "\n此程序的运行时间为" << totaltime << endl;
system("pause");
return 0;
}
[源码请戳](https://github.com/MarcsOne/gitLearning/tree/master/%E6%A8%A1%E6%9D%BF%E7%AE%97%E6%B3%95) 而结合**回溯法与模板算法**的具体实现思路是这样子的:首先回溯算法生成的不再是直接的数独矩阵,而是数独矩阵的模板,再产生随机的9个随机数填入模板中,一个模板矩阵可以生成 **8!**个随机数独,但是模板算法的一大弊端是**生成的随机矩阵有很大的可能会产生重复,但是结合模板算法可以很大的提高性能**,因此我采用了折中的方法,即**每个模板只产生k个随机矩阵,k越小重复的概率就越低,但是运行时间会加大;然而k越大重复的概率就越高,运行时间会变小。** **在代码中,每个模板矩阵的生成矩阵规模GRAND我取30,经过概率论的相关计算得出,0.0744%的概率会产生重复的矩阵,即如果要生成100万个数独,平均重复数独个数为744个。** [相关代码请戳](https://github.com/MarcsOne/gitLearning/tree/master/SudokuProject1)
测试运行以及相关说明
- 纯回溯法的情况下:
详细代码请戳- 模板算法的情况下:
由于第二种只是临时写了简单的代码,便没有加上文件的输出,经过网上查阅,文件的输出比cmd的输出快得多,因此总体上,第二种方法的速度是比第一种高的多的,但是第二种仅能生成40320种数独(在右上角第一个数固定的情况下,如果没有固定则可以生成9X40320种数独)。
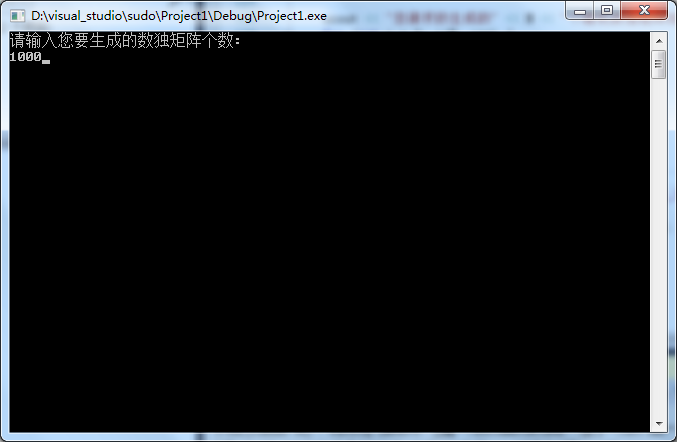
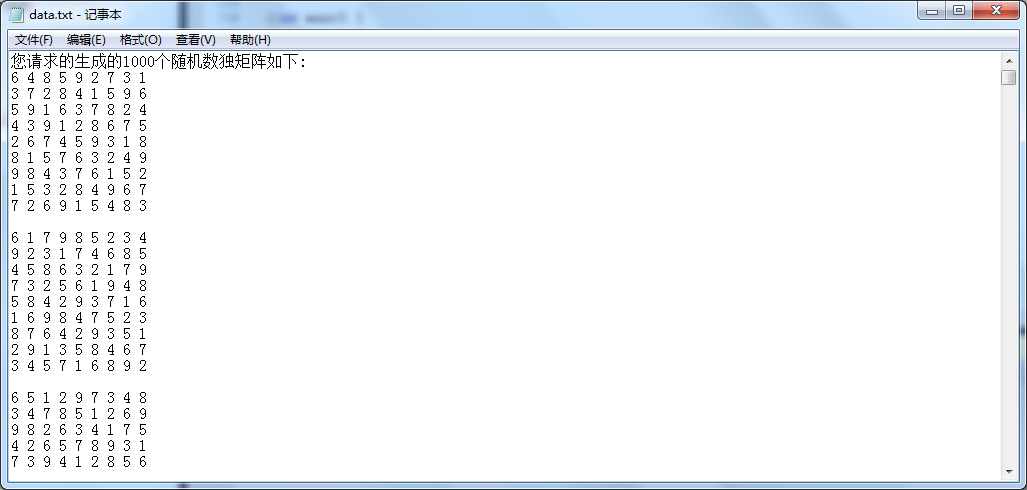
现在来看看回溯法+模板法,并且在重复概率为0.0744%的情况下的运行生成100万个随机矩阵的结果:
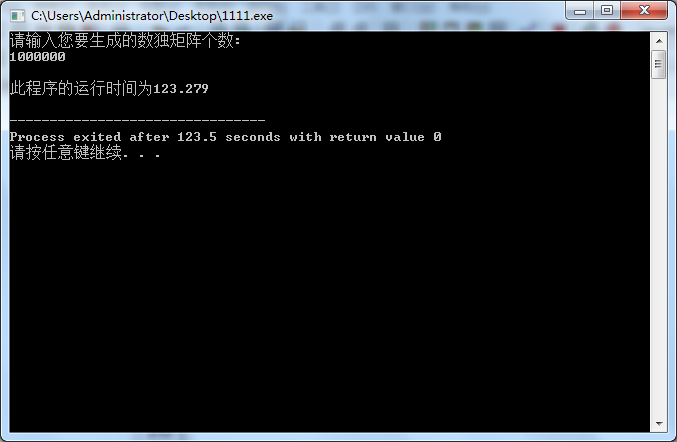
单元测试以及性能分析和改进
针对于回溯法,单元测试如下:
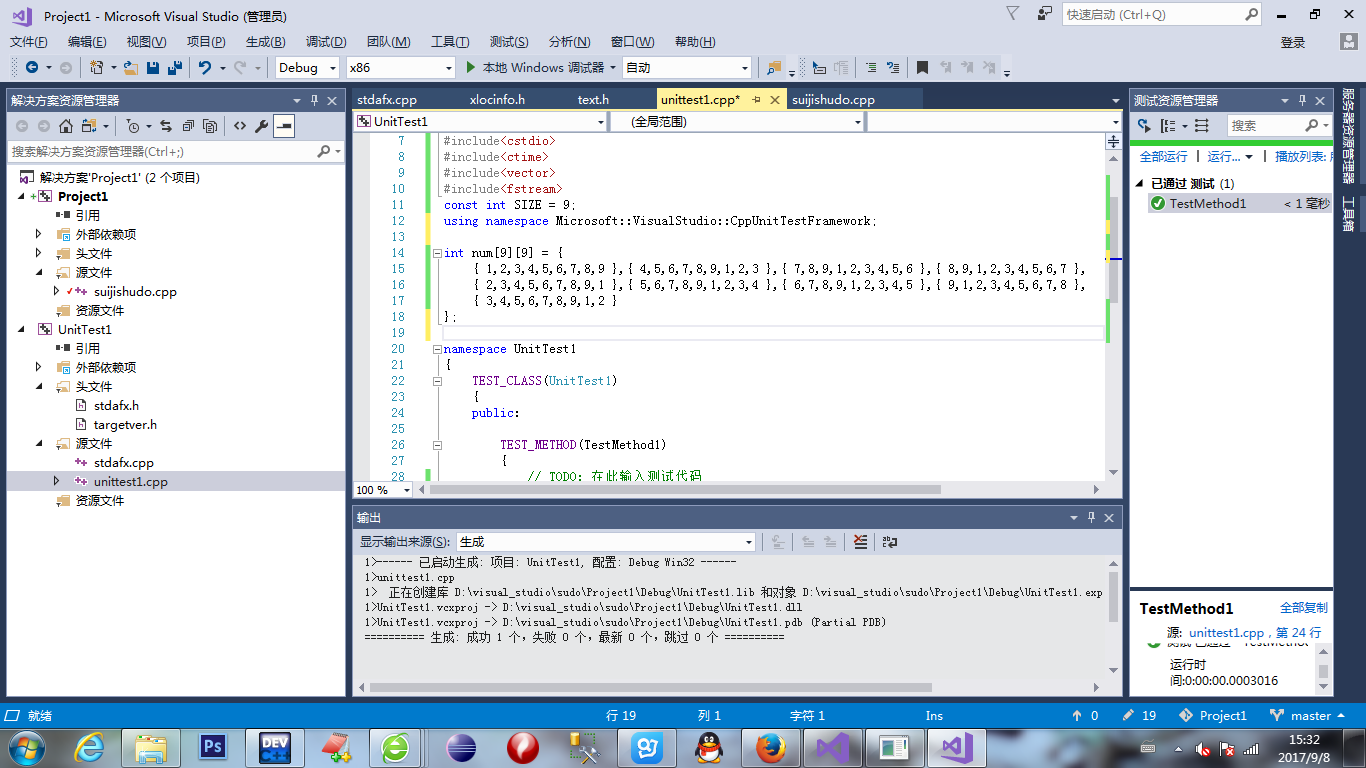
性能分析如下:
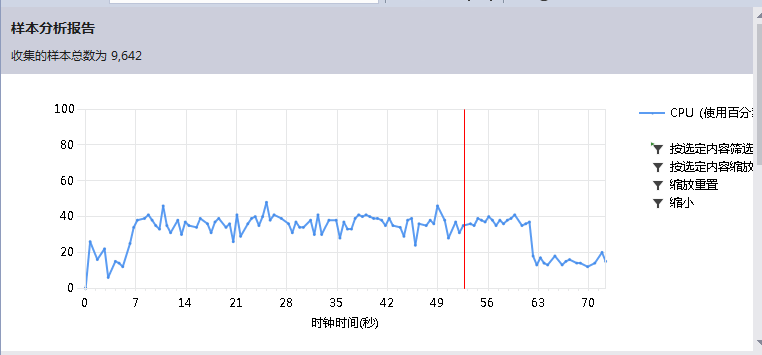
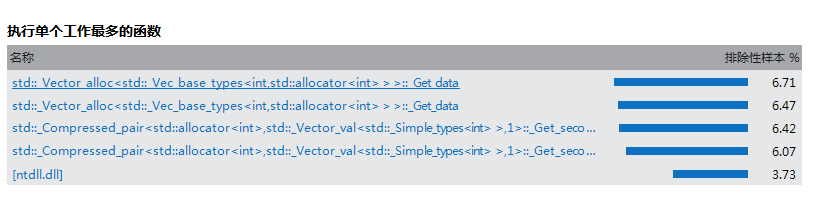
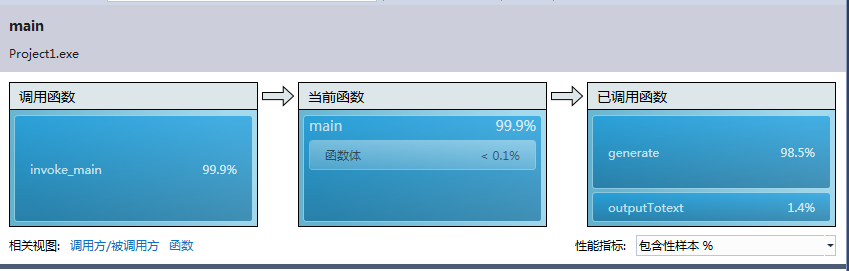
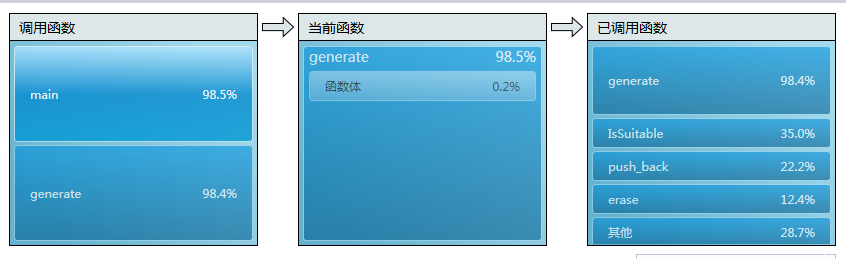
从图中可以看出generator占用极大,IsSuitable次之,其中generator主要在递归时占用最大,其中采用如上矩阵变化+回溯法的思想,成功实现话可以降低generator的递归次数以此来提高效率(很可惜由于个人能力有限,我未能实现出来),另外IsSuitable中尽量避免变量的重复定义也可以提高效率,其中有实现的就是之前写代码的时候前面num[0][0]每次都重新判断是否i0并且j0,现在直接初始化的时候就固定num[0][0]的值。原本考虑提高vector 的push_back的速度,但是经网上查阅无果。
改动:已实现回溯法+模板法思路如上所示。
代码见我的github。
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 40 | 45 |
| · Estimate | · 估计这个任务需要多少时间 | 1200 | 2520 |
| Development | 开发 | 180 | 235 |
| · Analysis | · 需求分析 (包括学习新技术) | 35 | 45 |
| · Design Spec | · 生成设计文档 | 20 | 15 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 15 | 20 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 15 | 20 |
| · Design | · 具体设计 | 60 | 75 |
| · Coding | · 具体编码 | 320 | 260 |
| · Code Review | · 代码复审 | 20 | 40 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 120 | 98 |
| Reporting | 报告 | 120 | 180 |
| · Test Report | · 测试报告 | 23 | 35 |
| · Size Measurement | · 计算工作量 | 15 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 35 | 60 |
| 合计 | 2218 | 3668 |
总结
这次项目实践算是在计算机软件这条路上走的第一步吧,虽然自我感觉难度有点大(毕竟很多东西不了解,比如git,github,markdown,以及visual studio以及单元测试,性能分析等工具的使用,大神忽略),可能做得不够圆满,但是至少我独立算是勉强完成了一次实践,希望自己在以后的路上可以越走越远,学到更多东西,丰富自己。(感谢助教和老师们的指导)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号