「杂题乱刷2」CF750F

题目链接

CF750F New Year and Finding Roots *2800

解题思路

hint1

考虑将不同的节点类型分类。

hint2

考虑将不同度数的节点分类。

算法 1：

首先我们注意到度数为 \(2\) 的节点为根，于是我们直接 check 每个节点，特别的，可以不用 check 最后一个节点，因为若前面的节点均不为答案，则最后一个节点一定为答案，那么这样操作次数是 \(2^h - 2\) 次，可以通过 \(h \le 4\) 的数据。

hint3

我们可以知道一个节点的深度吗？

hint4

我们可以知道一个节点是否是另一个节点的祖先吗？

算法 2：

结合 hint3 思考，发现我们完全可以知道一个节点的深度是多少，我们只需要找到两个叶子节点即可，那么这样即可知道这条路径上的所有节点的深度，具体实现方式就是先顷定从这个点开始的行走路径不经过重复的节点，然后按照这个约束直接跑 dfs 即可，细节要注意开始询问的第一个节点就是叶子结点。

考虑 hint4 中如何判断一个点 \(x\) 是否是另一个点 \(y\) 的父亲，我们只需要在 \(x\) 上搜一个路径，直到搜到一个叶子结点为止，如果搜的次数多，说明往上爬了，不劣，否则一定是一直往更深的节点走的，因为你是从父亲开始搜下来的，那么判断是否为父亲的方式就是你设点 \(y\) 的深度为 \(d\)，从 \(x\) 开始搜索时搜索序列长度是否最终不是 \(d - 1\) 即可。

因为如果 \(x\) 是 \(y\) 的父亲的话，那么这个搜索序列长度不可能是 \(d - 1\)，因为此时 \(x\) 到叶子节点的距离为 \(d - 1\)，整个路径至少需要遍历 \(d\) 个点。

否则，若 \(x\) 不是 \(y\) 的父亲。那么此时 \(y\) 为 \(x\) 的父亲，那么从 \(x\) 这个点开始往下搜显然不可能再次往上，因为父亲为 \(y\)，路径上不能有重复的节点。

考虑这个做法操作次数是多少，考虑到当 \(h = 7\) 且你得到的 lca 深度为 \(5\) 的时候这个做法是很劣的，具体操作次数为 \(5 + 4 + 5 + 6 + 1 = 21\) 次。

hint5

发现当一个节点深度较小的时候我们判断一个节点是否是另一个节点的祖先所需要的代价是非常高的，考虑优化这个东西。

算法 3：

我们可以发现当我们搜到了深度 \(\le 3\) 的节点时，后面再执行找叶子结点的操作显然已经不优了，发现我们直接 bfs 与当前这个点距离 \(\le 2\) 的节点即可。

那么此时我们的具体操作次数为 \(6 + 11 = 17\) 次，仍然不能通过此题。

然后为了便于大家理解，我就放张图片吧，加粗的节点为需要询问的节点，这张图片为初始询问节点为叶子结点的情况，容易发现这种情况操作次数是最多的，数一下也能发现询问次数是 \(17\) 次。

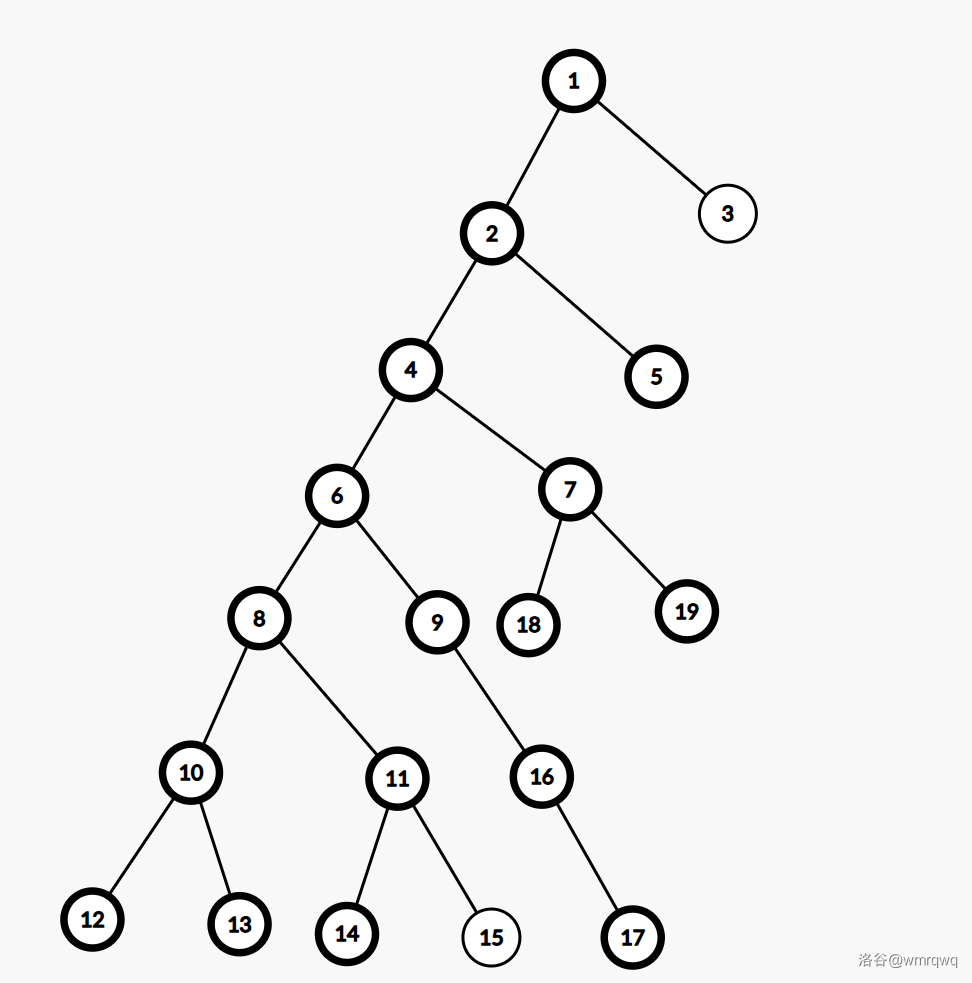
hint6

你注意到算法 1 中加粗的文字了吗，考虑用这种方式优化。

算法 4：

保留算法 3 的做法，发现最后一次询问是一个无效操作，你的最后一次询问一定是根节点，于是你在 \(\ge 17\) 次之后的所有询问都顷定这次询问的节点为答案即可。

询问次数为 \(17 - 1 = 16\) 次，可以通过此题。

参考代码

ll h;
ll S;
vector<ll>G[100010];
vector<ll>ask(ll x)
{
    if(!G[x].empty())
        return G[x];
    S++;
    if(S>16)
    {
        vector<ll>v;
        v.pb(0);
        v.pb(0);
        return v;
    }
    cout<<"? "<<x<<endl;
    ll k;
    cin>>k;
    vector<ll>v;
    forl(i,1,k)
        v.pb(rd());
    for(auto i:v)
        G[x].pb(i);
    return v;
}
vector<ll>now1,now2;
ll Dfs(ll x)
{
    now1.pb(x);
    vector<ll>v=ask(x);
    if(v.size()==2)
        return x;
    for(auto i:G[x])
        if(G[i].empty())
            return Dfs(i);
    return 0;
}
ll bfs(ll x)
{
    ll rt;
    for(auto i:G[x])
        if(G[i].empty())
            rt=i;
    queue<ll>q;
    q.push(rt);
    forl(i,1,h*2)
    {
        ll now=q.front();
        q.pop();
        vector<ll>V=ask(now);
        if(V.size()==2)
            return now;
        if(i>=h)
            continue;
        for(auto i:G[now])
            if(G[i].empty())
                q.push(i);
    }
    return 0;
}
void solve()
{
    S=0;
    cin>>h;
    forl(i,1,pw(h)-1)
        G[i].clear();
    vector<ll>v1=ask(1);
    if(v1.size()==2)
    {
        cout<<"! "<<1<<endl;
        return ;
    }
    ll st=1,d=h;
    if(v1.size()==3)
    {
        now1.clear();
        now2.clear();
        for(auto i:v1)
        {
            ll now=Dfs(i);
            if(now)
            {
                cout<<"! "<<now<<endl;
                return ;
            }
            if(now2.empty())
                swap(now1,now2);
            else
            {
                if(now1.size()<now2.size())
                    swap(now1,now2);
                d=h-now2.size();
                if(now1.size()==now2.size())
                    break;
                st=(h-d+now1.size())/2-(h-d)-1;
                d-=st+1;
                st=now1[st];
                break;
            }
        }
    }
    ll lim=min(4ll,h);
    while(d>lim)
    {
        now1.clear();
        ll now=Dfs(st);
        if(now)
        {
            cout<<"! "<<now<<endl;
            return ;
        }
        st=(h-d+now1.size())/2-(h-d);
        d-=st;
        st=now1[st];
    }
    ll ans=bfs(st);
    cout<<"! "<<ans<<endl;
}