BalticOI 2014「Three Friends」

Three Friends

这是一道HASH练习题，但我觉得十分有历史记录价值，（因为这是我第一次通过手推出一些公式来达到O（n））

题目大意

把一个字符串复制一遍接到原串后面，再插入一个字符到这个新串的某个位置。现在告诉你新串及插入的字符，求原串。

思路

根据题目意思，我们可以先求出字符串的HASH是，再枚举插入字符的位置然后判断字符串去掉这个字符后，用HASH计算两串是否相等的办法，判断能否分成两个相同部分。
这时，会有三种情况，如图：

我们枚举插入字符的位置并判断左半串和右半串是否相等。

（\(i\)表示当前枚举到的位置，\(A\)数组为\(S\)串的HASH值，\(len\)为\(S\)的长度，\(P_{i}\)表示\(b\)(常数)的\(i\)次方）

1、插入字符在左半边时：\(A[i-1]*P[(len+1)/2-i]+A[(len+1)/2]-A[i]*P[(len+1)/2-i]\)应等于\(A[len]-A[(len+1)/2]*P[len/2]\)>

2、插入字符在左半边时：\(A[len/2]\)应等于\((A[i-1]-A[len/2]*P[i-1-len/2])*P[len-i]+A[len]-A[i]*P[len-i]\)

3、插入字符在中间时：\(A[len/2]\)应等于\(A[len]-A[(len+1)/2]*P[len-i]\)
为什么呢？

让我们来看看情况1的左半串：
\(A[i-1]*P[(len+1)/2-i]+A[(len+1)/2]-A[i]*P[(len+1)/2-i]\)

它是如何组合出来的呢？

首先我们已经求出了\(S\)串的HASH值\(A\)，

如图：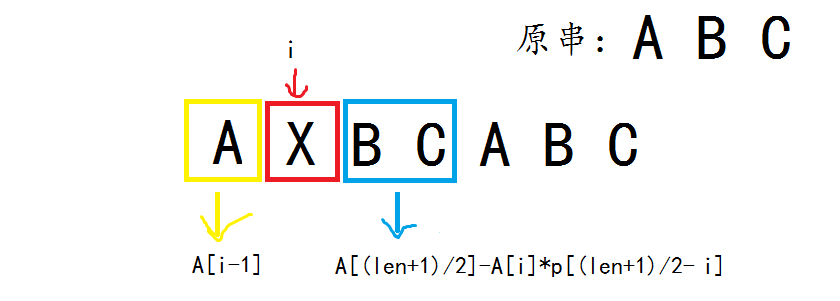
当我们已经得到黄框框和蓝框框的HASH值时(设为\(X\)和\(Y\))，如何把他们合并成为一个串呢？让我们回想一下一开始求原串的HASH值时的做法：先将黄框框的值乘以\(b\)（常数），再加上蓝框框的第一个字符，然后再乘\(b\)，再加上下一个字符。现在，已经知道蓝框框的HASH值了，设蓝框框的长度为\(l\)，那原来的计算式子\(((X*b+Y_{1})*b+Y_{2})*b+...+Y_{l}\)就变成了\(X*P_{l} +(Y_{1}*b+Y_{2})*b+...+Y_{l}\),其中，\((Y_{1}*b+Y_{2})*b+...+Y_{l}\)正好是蓝框框的HASH值，所以我们只要预处理好\(P\)数组，就可以\(O（1）\)组合出一个串的HASH并进行比较了。

其余的情况也类似，有插入字符的一边用上述方法组合成一个串，另一边直接用普通的计算HASH值的方法求出HASH值，再比较就能判断当前的\(i\)是不是插入字符的位置了。

code

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef unsigned long long ll;
char s[2100000];
ll len,ans,sum,x,b=1e9+7,p[2100000],a[2100000];
int main()
{
	scanf("%lld%s",&len,s+1);
	if(len%2==0)
	{
		printf("NOT POSSIBLE\n");
		return 0;
	}
	p[0]=1;
	a[0]=ans=0;
	for(int i=1;i<=len+10;i++)
	p[i]=p[i-1]*b;
	for(int i=1;i<=len;i++)
	a[i]=a[i-1]*b+s[i];
	for(int i=1;i<=len;i++)
	{
		bool bk=false;
		if(i<(len+1)/2)
		{
			if(a[i-1]*p[(len+1)/2-i]+a[(len+1)/2]-a[i]*p[(len+1)/2-i]
			==a[len]-a[(len+1)/2]*p[len/2])
			sum=a[len]-a[(len+1)/2]*p[len/2],x=i,bk=true;
		}
		else
		if(i>(len+1)/2)
		{
			if(a[len/2]
			==(a[i-1]-a[len/2]*p[i-1-len/2])*p[len-i]+a[len]-a[i]*p[len-i])
			sum=a[len/2],x=i,bk=true;
		}
		else
		if(i==(len+1)/2)
		{
			if(a[len/2]==a[len]-a[(len+1)/2]*p[len-i])
			sum=a[len/2],x=i,bk=true;
		}
		if(ans&&bk)
		{
			if(ans!=sum)
			{
				printf("NOT UNIQUE\n");
				return 0;
			}
		}
		else
		ans=sum;
	}
	if(!ans)
	printf("NOT POSSIBLE\n");
	else
	{
		for(int i=1;i<=len/2;i++)
		{
			if(i<x)
			printf("%c",s[i]);
			else
			printf("%c",s[i+1]);
		}
		printf("\n");
	}
	return 0;
}