函数对称性的应用及判断

前言

当你学习了本篇博文后，如果感觉还需要深入学习，可以阅读函数的对称性习题；

常见结论

• 注意：此时只涉及一个函数，是函数自身具有的对称性，而不是两个函数之间的对称；

1、若函数\(y=f(x)\)关于原点\((0，0)\)对称，则\(f(-x)=-f(x)\)或\(f(x)+f(-x)=0\)，反之亦成立；

2、若函数\(y=f(x)\)关于直线\(x=a\)对称，则\(f(a+x)=f(a-x)\)，反之亦成立；

3、若函数\(y=f(x)\)满足\(f(a+x)=f(b-x)\)，则其图像关于直线\(x=\cfrac{a+b}{2}\)对称，反之亦成立；

4、若函数\(y=f(x)\)图像是关于点\(A(a，b)\)对称，则充要条件是\(f(x)+f(2a-x)=2b\)。

给出方式

• 1、以图像的形式给出；

解读图像，从图像中我们就可以找出对称轴。

• 2、以奇偶性的形式给出[奇偶性是对称性的特例]；

比如奇函数，\(f(-x)=-f(x)\)或者\(f(-x)+f(x)=0\Longrightarrow\) 对称中心为\((0，0)\)

比如偶函数，\(f(-x)=f(x)\)或者\(f(-x)-f(x)=0\Longrightarrow\) 对称轴为\(x=0\)

• 3、以奇偶性的拓展形式给出；

比如\(f(2+x)+f(-x)=2\)，则对称中心为\((1，1)\)；

比如\(f(x)=f(4-x)\)，则对称轴为\(x=2\)，原因解释

• 4、以周期性+奇偶性的形式给出；

如，已知函数\(f(x)\)是奇函数，且满足\(f(x+4)=-f(x)\)，

则由\(\begin{align*} f(x+4)&=-f(x) \\ f(-x)&=-f(x)\end{align*}\) \(\big\}\Longrightarrow f(x+4)=f(-x)\Longrightarrow\)对称轴是\(x=2\)

对称性应用

【2016高考理科数学全国卷2第12题】【共用对称中心】已知函数\(f(x)(x\in R)\)满足\(f(-x)=2-\) \(f(x)\)，若函数\(y=\cfrac{x+1}{x}\)与函数\(y=f(x)\)图像的交点为\((x_1，y_1)\)，\((x_2，y_2)\)，\(\cdots\)，\((x_m，y_m)\)，则\(\sum\limits_{i=1}^m{(x_i+y_i)}\)的值为【\(\qquad\)】

$A.0$ $B.m$ $C.2m$ $D.4m$

分析：由题目可知\(f(x)+f(-x)=2\)，即函数\(f(x)\)图像关于点\((0，1)\)对称，

而函数\(y=\cfrac{x+1}{x}=1+\cfrac{1}{x}\)图像也关于点\((0，1)\)对称，即两个函数图像有相同的对称中心，

那么二者的交点个数一定有偶数个，如图所示， 可知对横坐标而言有\(\sum\limits_{i=1}^m{x_i}=0\)，

而对纵坐标而言，成对的点的个数是\(\cfrac{m}{2}\)个，他们中的每一对满足\(\cfrac{y_1+y_m}{2}=1\)，

即\(y_1+y_m=2\)，故\(\sum\limits_{i=1}^m{y_i}=2\cdot \cfrac{m}{2}=m\)，

故\(\sum\limits_{i=1}^m{(x_i+y_i)}=\sum\limits_{i=1}^m{x_i}+\sum\limits_{i=1}^m{y_i}=m\)，故选 \(B\) .

【2016高考文科数学全国卷2第12题】【共用对称轴】已知函数\(f(x)(x\in R)\)满足\(f(x)=\) \(f(2-x)\)，若函数\(y=|x^2-2x-3|\)与函数\(y=f(x)\)图像的交点为\((x_1，y_1)\)，\((x_2，y_2)\)，\(\cdots\)，\((x_m，y_m)\)，则\(\sum\limits_{i=1}^m{x_i}\)的值为 【\(\qquad\)】

$A.0$ $B.m$ $C.2m$ $D.4m$

分析：函数\(f(x)(x\in R)\)满足\(f(x)=f(2-x)\)，则函数的对称轴是直线\(x=1\)，

而函数\(y=|x^2-2x-3|=|(x-1)^2-4|\)的对称轴也是直线\(x=1\)，作出函数的图像如右图所示，

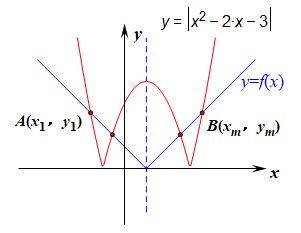
则二者的交点个数\(m\)一定是偶数个，两两配对的个数为\(\cfrac{m}{2}\)，比如\(A\) \(B\)配对，

则有\(\cfrac{x_1+x_m}{2}=1\)，\(x_1+x_m=2\)，故\(\sum\limits_{i=1}^m{x_i}=\cfrac{m}{2}\cdot 2=m\)，故选\(B\)。

对称性判断

【2017全国卷1文科第9题高考真题】已知函数\(f(x)=lnx+ln(2-x)\)，则【\(\qquad\)】

$A.$在$(0，2)$上单调递增

$B.$在$(0，2)$上单调递减

$C.y=f(x)$的图像关于直线$x=1$对称

$D.y=f(x)$的图像关于点$(1，0)$对称

分析：由于函数\(f(x)\)是复合函数，定义域要使\(x>0，2-x>0\)，即定义域是\((0，2)\)，

又\(f(x)=ln[x(2-x)]=ln[-(x-1)^2+1]\)，则由复合函数的单调性法则可知，

在\((0，1)\)上单增，在\((1，2)\)上单减，故排除\(A\)，\(B\)；

若函数\(y=f(x)\)关于点\((1，0)\)对称，则函数\(f(x)\)必然满足关系：\(f(x)+f(2-x)=0\)；

若函数\(y=f(x)\)关于直线\(x=1\)对称，则函数\(f(x)\)必然满足关系：\(f(x)=f(2-x)\)；

接下来我们用上述的结论来验证，由于\(f(x)=lnx+ln(2-x)\)，

\(f(2-x)=ln(2-x)+ln(2-(2-x))=ln(2-x)+lnx\)，即满足\(f(x)=f(2-x)\)，故函数\(y=f(x)\)的图像关于直线\(x=1\)对称，选\(C\)；

再来验证\(D\)，发现\(f(x)+f(2-x)=2[lnx+ln(2-x)]\neq 0\)，\(D\)选项不满足。故选\(C\)。

【2019会宁模拟】已知函数\(f(x)\)的定义域为\(R\)，且在\([0,+\infty)\)上单调递增，\(g(x)=-f(|x|)\)，若\(g(lgx)>g(1)\)，则\(x\)的取值范围为【\(\qquad\)】

$A.(0,10)$ $B.(10,+\infty)$ $C.(\cfrac{1}{10},10)$ $D.(0,\cfrac{1}{10})\cup (10,+\infty)$

分析：由于函数\(f(x)\)的定义域为\(R\)，且在\([0,+\infty)\)上单调递增，

故函数\(g(x)=-f(|x|)\)在\([0,+\infty)\)上单调递减，且为偶函数，

故\(g(lgx)>g(1)\)即可以变形为\(g(|lgx|)>g(1)\)，则由单调性可知，

\(|lgx|<1\)，即\(-1<lgx<1\)，解得\(\cfrac{1}{10}<x<10\)，故选\(C\)。

【2019届高三理科数学三轮模拟题】已知函数\(f(x)=e^x+e^{2-x}\)，则\(f(x)\) 【\(\qquad\)】

$A.$在$R$上递增

$B.$在$R$上递减

$C.$关于点$(1，2e)$对称

$D.$关于直线$x=1$对称

提示：由于函数满足\(f(x)=f(2-x)\)，故函数\(f(x)\)关于直线\(x=1\)对称，选\(D\)。

引申：\(f(x)=e^x+e^{1-x}\)；\(g(x)=e^x+e^{-x}\)；

【2018高三文科训练题】已知函数\(f(x)=lg(4x-x^2)\)，则【\(\qquad\)】

$A.f(x)$在$(0，4)$上单调递增

$B.f(x)$在$(0，4)$上单调递减

$C.y=f(x)$的图像关于直线$x=2$对称

$D.y=f(x)$的图像关于点$(2，0)$对称

分析：令内函数\(g(x)=4x-x^2>0\)，得到定义域\((0，4)\)，又\(g(x)=-(x-2)^2+4\)，故内函数在\((0，2]\)单减，在\([2，4)\)单增，外函数只有单调递增，故复合函数\(f(x)\)在\((0，2]\)单减，在\([2，4)\)单增，故排除\(A\)、\(B\)；

要验证\(C\)选项，只需要验证\(f(x)=f(4-x)\)即可，这是\(y=f(x)\)的图像关于直线\(x=2\)对称的充要条件；

而\(f(4-x)=lg[4(4-x)-(4-x)^2]=lg(16-4x-16+8x-x^2)=lg(4x-x^2)=f(x)\)，故选\(C\)。

若要验证\(D\)选项，只需要利用\(y=f(x)\)的图像关于点\((2，0)\)对称的充要条件，即验证\(f(x)+f(4-x)=0\)即可。自行验证，不满足。

故本题目选\(C\).

已知函数 \(f(x)=\ln x+\ln (a-x)\) 的图象关于直线 \(x=1\) 对称， 则函数 \(f(x)\) 的值域为 【\(\qquad\)】

$A.(0,2)$ $B.[0,+\infty)$ $C.(-\infty,2]$ $D.(-\infty, 0]$

解: 根据题意， 对于函数 \(f(x)=\ln x+\ln (a-x)\)，

有 \(f(a-x)=\ln (a-x)+\ln [a-(a-x)]=\ln x+\ln (a-x)=f(x)\)，即\(f(a-x)=f(x)\)，

则函数 \(f(x)\) 的图象关于直线 \(x=\frac{a}{2}\) 对称，

若函数 \(f(x)=\ln x+\ln (a-x)\) 的图象关于直线 \(x=1\) 对称，则有 \(\cfrac{a}{2}=1\)， 则 \(a=2\)，

则 \(f(x)=\ln x+\ln (2-x)=\ln \left(2 x-x^{2}\right)\)，其定义域为 \((0,2)\)，

设 \(t=2 x-x^{2}\)， 则 \(y=\ln t\)，

又由 \(t=-(x-1)^{2}+1\)，\(0<x<2\)， 则有 \(0<t\leqslant 1\)， 则 \(y=\ln t\leqslant 0\)，

即函数 \(f(x)\) 的值域为 \((-\infty, 0]\)， 故选: \(D\) .