复合函数
前言
复合函数是高中数学中的一大难点,那么什么是复合函数呢?就像我们学习集合的交集运算时,有 \(A\cap(B\cap C)\)一样(求完交集再求交集),由 \(x\rightarrow g(x)\)(对应),再由\(g(x)\rightarrow f[g(x)]\)(对应完后再对应),这样我们得到的函数 \(y=f[g(x)]\)就是复合函数。
复习准备
- 基本初等函数,可以类比原子是构成物质的最基本的不可再分的微粒一样,来理解基本初等函数和其他函数的关系。高中阶段所学习的函数中,只有前五种基本初等函数,需要学生切实掌握。第六种现在不需要学生学习。
①常函数\(f(x)=c(c\)为常数) ;
②幂函数\(f(x)=x^{\alpha}\) ;
③指数函数\(f(x)=a^x(a>0\)且\(a\neq 1)\) ;
④对数函数\(f(x)=log_ax(a>0\)且\(a\neq 1)\) ;
⑤三角函数\(f(x)=sinx\)或\(f(x)=cosx\) ;
⑥反三角函数\(f(x)=arcsinx,x\in[-\cfrac{\pi}{2},\cfrac{\pi}{2}]\)等 ,
- 初等函数:由基本初等函数经过四则运算所构成的函数。如一次函数,二次函数等。比如,一次函数\(f(x)=kx+b(k\neq 0)\),其实是常函数\(y=k\)与幂函数\(y=x\)相乘,再与常函数\(y=b\)求和得到的;比如,指数型函数\(y=3\cdot 2^x+1\),其实是常函数\(y=3\)与指数函数\(y=2^x\)相乘,再与常函数\(y=1\)求和得到的。
复合函数
高中阶段涉及到的复合函数,一般就由以上的基本初等函数或初等函数复合而成。为控制难度,一般大多只复合一次。
定义:设函数\(y=f(u)\)和\(u=g(x)\),则函数\(y=f[g(x)]\)称为由\(y=f(u)\)和\(u=g(x)\)复合而成的复合函数,其中函数\(y=f(u)\)常常称为外函数,函数\(u=g(x)\)常常称为内函数,其中内函数的值域必须是外函数的定义域的子集。
如何拆分
有时候,我们却需要将复合函数拆分开,以便于解决相应的问题。此时我们应该注意,要尽可能将函数拆分为为基本初等函数或初等函数。比如,给定函数如\(y=(\cfrac{1}{2})^{2x^2+3x-1}\),我们就拆分为\(y=(\cfrac{1}{2})^u\)和\(u=2x^2+3x-1\)两个函数。
典例剖析
- 涉及复合函数+抽象函数的定义域,需要注意以下几点:
①比如 \(f(x)\) 与 \(f(x+2)\) 和 \(f(2^x-3)\) 中,由于自变量 \(x\) 与 \(x+2\) 和 \(2^x-3\) (此处需要将 \(x+2\) 和 \(2^x-3\)分别看成一个整体对待,比如 \(t=x+2\) 或 \(t=2^x-3\))接受同样的对应关系的作用,故所受的限制应该是一样的,即三个自变量(或自变量的整体)的取值范围应该是一样的;举个实际例子,三个自变量 \(x\) 与 \(x+2\) 和 \(2^x-3\)就类似一个班级里的某个单个人,某个小组,某个组织等,它们都应该接受这个班级的纪律约束(就类似对应关系 \(f\) )一样.
②已知定义域或求解定义域都是针对单独的自变量 \(x\) 而言。
分析:解决这类题目需要牢牢抓住两点:其一接受对应法则\(f\)作用的\(x\)和\(2x+1\)是处于对等位置的,其二不论是给定函数的定义域还是求解函数的定义域,都是针对单独的自变量\(x\)而言,
据此可知由于\(-1\leq x\leq 1\),
故\(-1\leq 2x+1\leq 1\),解得\(x\in [-1,0]\),
故复合函数\(f(2x+1)\)的定义域是\(x\in [-1,0]\)。
分析:这里同样你得清楚\(x+1\)和\(2^x-2\)是对等的,
先由\(x\in[0,1]\),计算得到\(1\leq x+1\leq 2\),故\(1\leq 2^x-2\leq 2\),
解得\(3\leq 2^x\leq 4\),同时取以2为底的对数得到\(log_2^3\leq x\leq 2\),
则所求定义域是\(x\in [log_2^3,2]\)。
分析:由上面的例子分析可知,所给函数的定义域是\([-1,1]\),
即函数\(f(2x+1)\)的自变量\(x\)的取值范围是\([-1,1]\),
故内函数\(2x+1\)的取值范围这样求解,
由\(-1\leq x \leq 1\),得到\(-2\leq 2x \leq 2\),
所以\(-1=-2+1\leq 2x+1 \leq 2+1=3\),
又由于\(2x+1\)和\(x\)对等(你可以理解为这两个接受同样的纪律约束也行),
所以\(f(x)\)的\(x\)的取值范围应该是\(-1\leq x\leq 3\),
故函数\(f(x)\)的定义域是\([-1,3]\)。
- 复合函数的值域
分析:设\(g(x)=sinx+cos^2x-1\),\(x\in (0,\cfrac{\pi}{2})\),则\(g(x)=sinx-sin^2x=-(sinx-\cfrac{1}{2})^2+\cfrac{1}{4}\),
又\(0<sinx<1\),故当\(sinx=\cfrac{1}{2}\)时,\(g(x)_{max}=\cfrac{1}{4}\),即\(0<g(x)\leqslant \cfrac{1}{4}\),
故\(f(x)=log_{0.5}g(x)\geqslant log_{0.5}\cfrac{1}{4}=2\),故\(f(x)\in [2,+\infty)\)。
解: 根据题意, 对于函数 \(f(x)=\ln x+\ln (a-x)\),
有 \(f(a-x)=\ln (a-x)+\ln [a-(a-x)]=\ln x+\ln (a-x)=f(x)\),即\(f(a-x)=f(x)\),
则函数 \(f(x)\) 的图象关于直线 \(x=\frac{a}{2}\) 对称,
若函数 \(f(x)=\ln x+\ln (a-x)\) 的图象关于直线 \(x=1\) 对称,则有 \(\cfrac{a}{2}=1\), 则 \(a=2\),
则 \(f(x)=\ln x+\ln (2-x)=\ln \left(2 x-x^{2}\right)\),其定义域为 \((0,2)\),
设 \(t=2 x-x^{2}\), 则 \(y=\ln t\),
又由 \(t=-(x-1)^{2}+1\),\(0<x<2\), 则有 \(0<t\leqslant 1\), 则 \(y=\ln t\leqslant 0\),
即函数 \(f(x)\) 的值域为 \((-\infty, 0]\), 故选: \(D\) .
- 复合函数的单调性
分析:令\(u=x^2-3x+2\),则原复合函数拆分为外函数\(y=f(u)=log_2u\)和内函数\(u=x^2-3x+2\)
由\(u=x^2-3x+2>0\),解得\(x\in (-\infty,1)\cup(2,+\infty)\),
即此复合函数的定义域为\(x\in (-\infty,1)\cup(2,+\infty)\)。
那么要研究其单调性,必须先在上述定义域范围内,定义域优先原则。
然后由\(u=x^2-3x+2=(x-\cfrac{3}{2})^2-\cfrac{1}{4}\),
则内函数\(u(x)\)在区间\((-\infty,1)\)上单调递减,在区间\((2,+\infty)\)上单调递增,
而外函数\(y=f(u)=log_2u\)只是单调递增的,
故复合函数\(f(x)\)在区间\((-\infty,1)\)上单调递减,在区间\((2,+\infty)\)上单调递增。
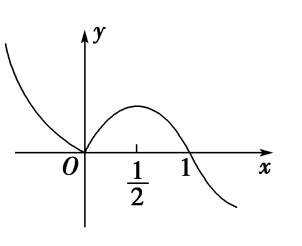
分析:由图可知,外函数\(f(x)\)在区间\((-\infty,0)\)和\([\cfrac{1}{2},+\infty)\)上单调递减,在区间\([0,\cfrac{1}{2}]\)上单调递增,
又\(0<a<1\)时,内函数\(y=log_ax\)在区间\((0,+\infty)\)上单调递减,
故要使得复合函数函数\(g(x)=f(log_ax)(0<a<1)\)单调递减,
则需要\(log_ax\in [0,\cfrac{1}{2}]\),即\(0\leq log_ax\leq \cfrac{1}{2}\),
解得\(x\in [\sqrt{a},1]\),故选\(B\)。
- 已知复合函数的单调性求参数的取值范围
分析:内函数\(g(x)=-(x-2)^2+9\),若要在区间\((a-1,a+1)\)上单调递减,
则内函数需要满足条件\(a+1\leq 2\)①;
又由于内函数必须恒为正,故需要满足\(-(a-1-2)^2+9\ge 0\)②,
联立①②可得,\(0\leq a\leq 1\);故选\(A\)。
分析:令\(g(x)=(a^2-3a)x\),由于\(g(x)>0\)在区间\((-\infty,0)\)上要恒成立,
则有\(a^2-3a<0\),这样内函数\(g(x)\)只能单调递减,复合函数\(f(x)=log_{3a}g(x)\)是单调递减的,
所以外函数必须是单调递增的,故\(3a>1\),由\(\begin{cases}a^2-3a<0\\3a>1\end{cases}\),
解得\(\cfrac{1}{3}<a<3\),故\(a\in(\cfrac{1}{3},3)\)。
解析:由于外函数的特性,\(a>0\) 且 \(a\neq 1\),且复合函数 \(f(x)=\log _{a}(6-ax)\) 为减函数,
故由复合函数的性质得 \(a>1\), 则由定义域可知 当 \(x \in[1,2]\) 时,由 \(6-a x>0\) 恒成立,
得到, \(6-2a>0\), 解得 \(a<3\);
又由于 \(2f(x)\leqslant 3^{\log _{3} 4}\) 恒成立, 即 \(f(x)\leqslant 2\) 恒成立.
即\(f(x)_{max}\leqslant 2\),又 \(f(x)_{max}=f(1)\),即得到 \(\log _{a}(6-a)\leqslant 2\)
即 \(\log _{a}(6-a)\leqslant \log_{a}a^2\),由于 \(a>1\),
得到 \(6-a\leqslant a^2\),解得 \(a\leqslant -3\)或 \(a\geqslant 2\)
综上所述,实数 \(a\) 的取值范围为 \([2,3)\).
分析:令内函数为\(g(x)=\cfrac{4x^2+m}{x}=4x+\cfrac{m}{x}\),借助对勾函数可知,
函数\(g(x)\)在\((0,\cfrac{\sqrt{m}}{2}]\)上单调递减,在\([\cfrac{\sqrt{m}}{2},+\infty)\)上单调递增;
由于复合函数\(f(x)\)在\([2,3]\)上单调递增,则可能有两种情形:
其一为外函数单调递减且内函数单调递减,其二为外函数单调递增且内函数单调递增,
则只需要满足\(\left\{\begin{array}{l}{0<m<1}\\{3\leqslant \cfrac{\sqrt{m}}{2}}\end{array}\right.\)或\(\left\{\begin{array}{l}{m>1}\\{\cfrac{\sqrt{m}}{2}\geqslant 2}\end{array}\right.\)
解得\(m\in \varnothing\)或\(1<m\leqslant 16\),即\(m\in (1,16]\),故选\(D\).
分析:令\(g(x)=6-ax\),像这类题目既要考虑单调性,还要考虑定义域,
易错之处就是只考虑单调性而不顾及定义域。
由题目可知必有\(a>0\),故函数\(g(x)\)单调递减,
考虑定义域时只要最小值\(g(2)>0\)即可,再考虑外函数必须是增函数,故\(a>1\),
结合\(g(2)>0\),解得\(1<a<3\),故选\(D\)。
- 复合函数的求导
分析:我们目前一般只涉及一次复合的函数如\(y=f(u)\)和\(u=g(x)\),则复合函数为\(y=f[g(x)]\),\([f(g(x))]'=f'[g(x)]\cdot g'(x)\);
令\(\phi=2x+1\),则\(y=f(x)=sin\phi\),故\(f'(x)=y'_x=y'_{\phi}\cdot \phi'_x=cos\phi\cdot 2=2cos(2x+1)\);
②设\(g(x)=ln(x^2+3x)\),求导函数\(g'(x)\);
分析:\(g'(x)=\cfrac{1}{x^2+3x}\cdot (x^2+3x)'=\cfrac{2x+3}{x^2+3x}\);
说明:函数\(f(x)=x^2\pm lnx\),不是复合函数,只是两个函数\(y=x^2\)与函数\(y=lnx\)之间用四则运算构成的一个新函数。
③[抽象复合函数的求导]设\(g(x)=x\cdot f(2x)\),求\(g'(x)\)
分析:\(g'(x)=[x\cdot f(2x)]'=x'\cdot f(2x)+x\cdot f'(2x)\cdot (2x)'=f(2x)+2x\cdot f'(2x)\)
- 注意:复合函数求导时的运算,如对\(y=ln(\cfrac{1+x}{1-x})\)直接求导,不如变形为\(y=ln(1+x)-ln(1-x)\)后求导;
若\(f(x)=cos(2x+\cfrac{\pi}{3})\),则\(f'(x)=-2sin(2x+\cfrac{\pi}{3})\);
若已知\(f(2x+3)\),则\([f(2x+3)]'=2f'(2x+3)\);
- 已知复合函数的定义域或值域为\(R\),求参数的取值范围;
①如果函数的定义域是\(R\),求参数\(a\)的取值范围;
预备:先想一想,这个函数的定义域应该怎么求解?
分析:由于函数的定义域是\(R\),说明对任意的\(x\in R\),都能使得\(g(x)=x^2+2ax-a>0\),
转化为二次函数恒成立问题了,(此时至少可以考虑数形结合或者恒成立分离参数)
这里用数形结合,函数\(g(x)\)开口向上,和\(x\)轴没有交点,则\(\Delta <0\),
即\(\Delta=(2a)^2-4\times 1\times(-a)<0\),解得\(a\in (-1,0)\)。
②如果函数的值域是\(R\),求参数\(a\)的取值范围;
分析:如右图所示,要使得函数\(f(x)\)的值域是\(R\),说明内函数\(g(x)=x^2+2ax-a\)必须要能取遍所有的正数,结合下图,
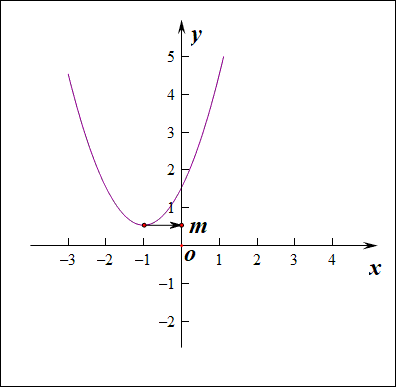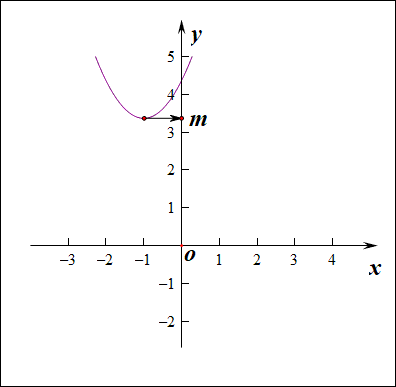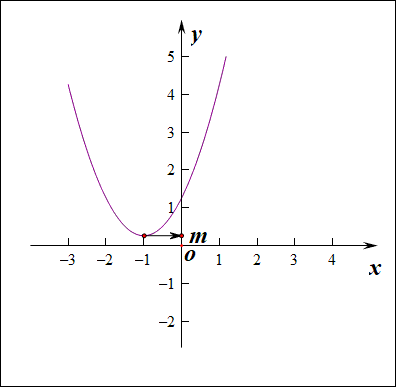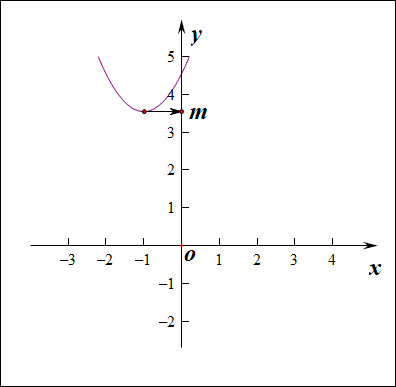
如果有一部分正实数不能取到,那么函数\(f(x)\)的值域就不会是\(R\),这样只能是函数\(g(x)\)的\(\Delta \ge 0\),
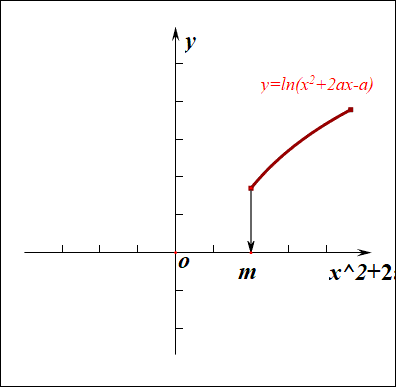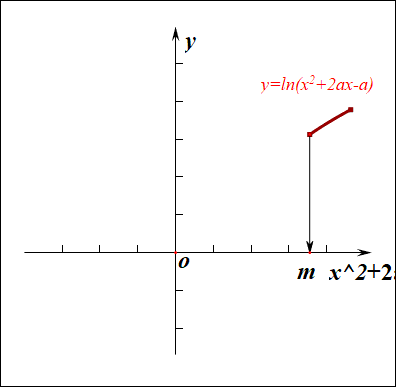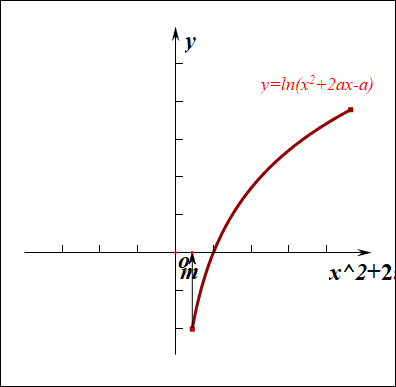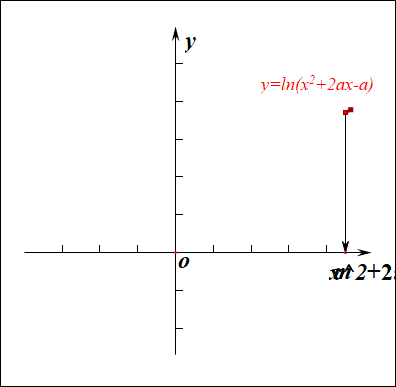
而不能是\(\Delta <0\),注意现在题目要求是值域为\(R\),而不是定义域为\(R\),
因此必须满足条件\(\Delta=(2a)^2-4\times 1\times(-a)\ge 0\),解得\(a\in \{a\mid a\leq -1 ,a\ge 0\}\)。
下图是参数\(a\in [-3,3]\)时的两个函数图像的动态变化情况;
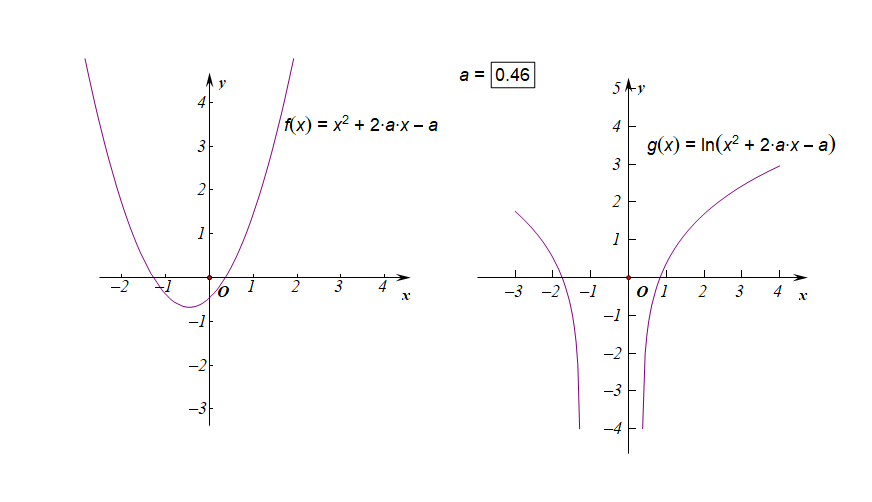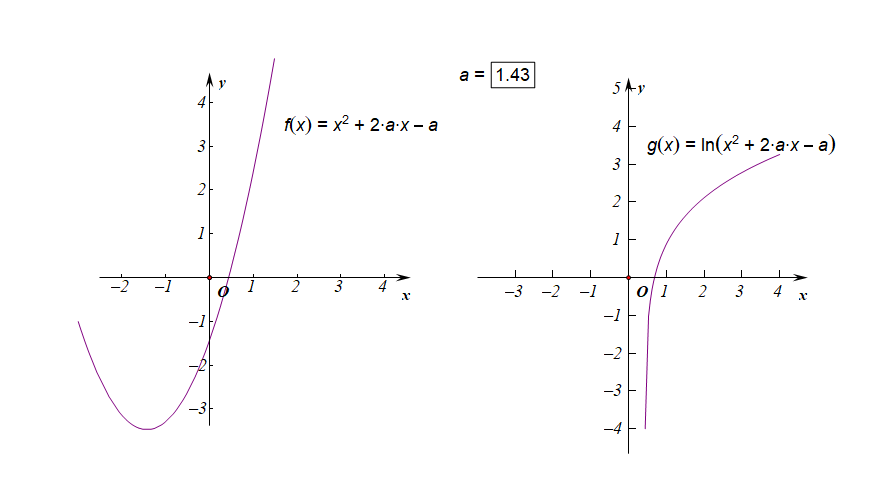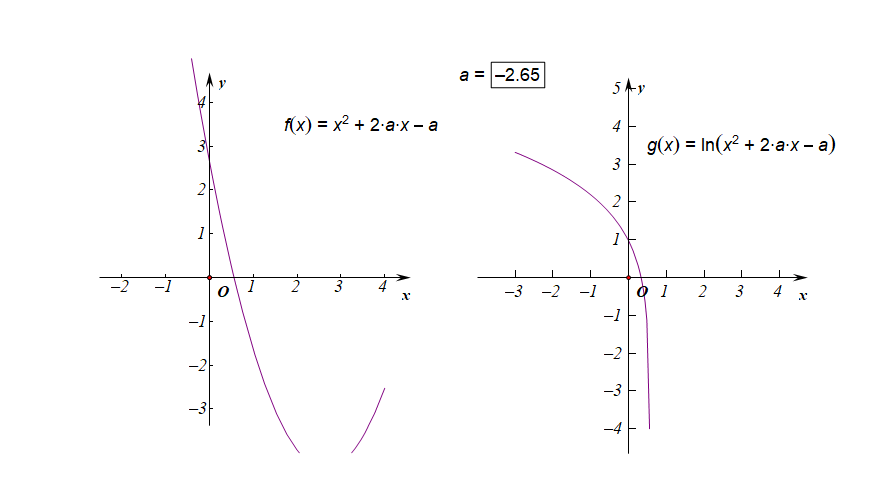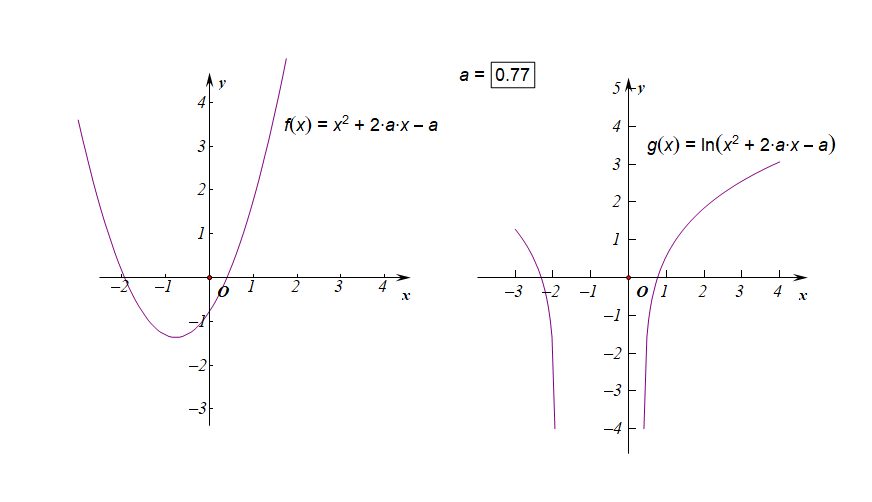
下图是参数\(a\in (-1,0)\)时的两个函数图像的动态变化情况;
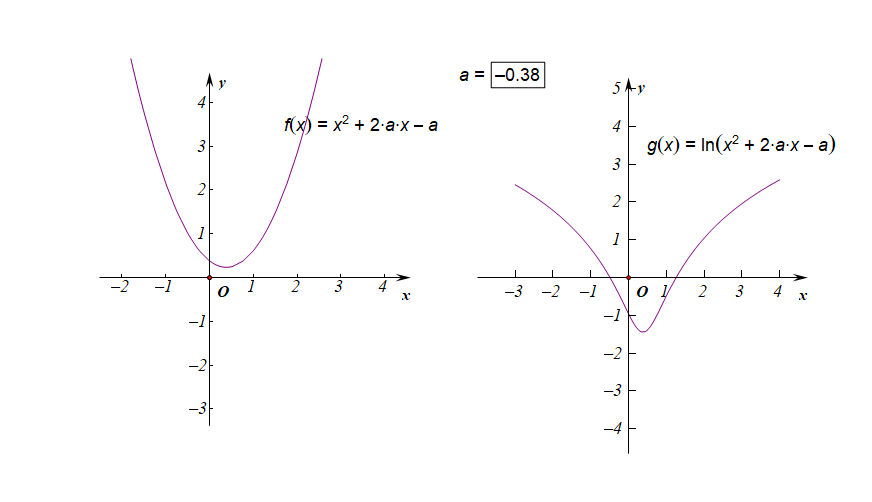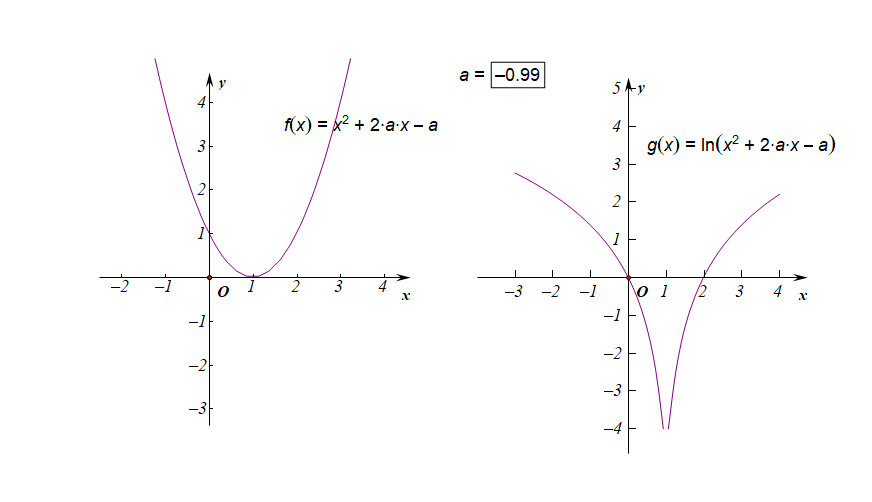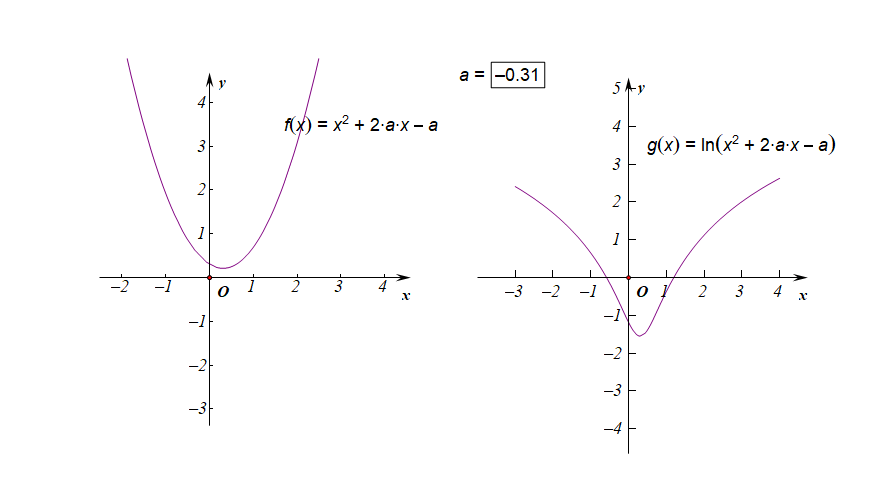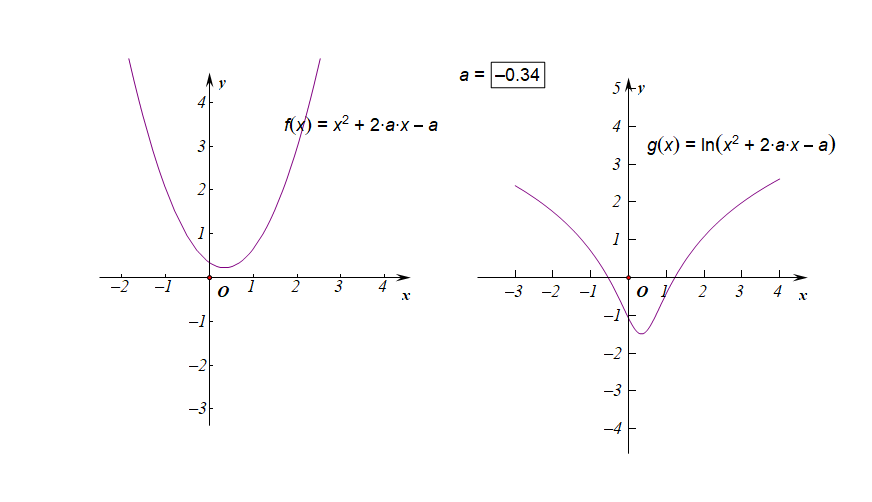

 将函数$y=f(u)$和$u=g(x)$经过一次复合而成$y=f[g(x)]$的形式,称为复合函数。
将函数$y=f(u)$和$u=g(x)$经过一次复合而成$y=f[g(x)]$的形式,称为复合函数。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号