三角函数知识点
前言
梳理、总结三角函数的常用的知识点,有助于相关运算。
人教2019版的正弦函数 \(y=\sin x\) 图象得到后,使用 \(\cos x=\sin(\cfrac{\pi}{2}+x)\) 将 \(y=\sin x\) 向左平移 \(\cfrac{\pi}{2}\) 得到 \(y=\cos x\) 的图象,不使用 \(\cos x=\sin(\cfrac{\pi}{2}-x)\) 的原因是,后者既涉及平移变换,还涉及对称变换,比较复杂。
必须熟记
- 特殊角的三角函数值,是三角函数学习的基础,必须熟练掌握。
| $$\theta(rad)$$ | \(0\)\(=\)\(0^{\circ}\) | \(\cfrac{\pi}{12}\)\(=\)\(15^{\circ}\) | \(\cfrac{\pi}{6}\)\(=\)\(30^{\circ}\) | \(\cfrac{\pi}{4}\)\(=\)\(45^{\circ}\) | \(\cfrac{\pi}{3}\)\(=\)\(60^{\circ}\) | \(\cfrac{5\pi}{12}\)\(=\)\(75^{\circ}\) |
|---|---|---|---|---|---|---|
| \(sin\theta\) | \(0\) | \(\cfrac{\sqrt{6}-\sqrt{2}}{4}\) | \(\cfrac{1}{2}\) | \(\cfrac{\sqrt{2}}{2}\) | \(\cfrac{\sqrt{3}}{2}\) | \(\cfrac{\sqrt{6}+\sqrt{2}}{4}\) |
| \(cos\theta\) | \(1\) | \(\cfrac{\sqrt{6}+\sqrt{2}}{4}\) | \(\cfrac{\sqrt{3}}{2}\) | \(\cfrac{\sqrt{2}}{2}\) | \(\cfrac{1}{2}\) | \(\cfrac{\sqrt{6}-\sqrt{2}}{4}\) |
| \(tan\theta\) | \(0\) | \(2-\sqrt{3}\) | \(\cfrac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | \(2+\sqrt{3}\) |
钝角的三角函数值需要注意负号;
| $$\theta(rad)$$ | $$\cfrac{\pi}{2}=90^{\circ}$$ | $$\cfrac{7\pi}{12}=105^{\circ}$$ | $$\cfrac{2\pi}{3}=120^{\circ}$$ | $$\cfrac{3\pi}{4}=135^{\circ}$$ | $$\cfrac{5\pi}{6}=150^{\circ}$$ | $$\pi=180^{\circ}$$ |
|---|---|---|---|---|---|---|
| \(sin\theta\) | \(1\) | \(\cfrac{\sqrt{6}+\sqrt{2}}{4}\) | \(\cfrac{\sqrt{3}}{2}\) | \(\cfrac{\sqrt{2}}{2}\) | \(\cfrac{1}{2}\) | \(0\) |
| \(cos\theta\) | \(0\) | \(-\cfrac{\sqrt{6}-\sqrt{2}}{4}\) | \(-\cfrac{1}{2}\) | \(-\cfrac{\sqrt{2}}{2}\) | \(-\cfrac{\sqrt{3}}{2}\) | \(-1\) |
| \(tan\theta\) | \(\infty\) | \(-(2+\sqrt{3})\) | \(-\sqrt{3}\) | \(-1\) | \(-\cfrac{\sqrt{3}}{3}\) | \(0\) |
记忆方法
| \(rad\) | \(0\) | \(\cfrac{\pi}{6}\) | \(\cfrac{\pi}{4}\) | \(\cfrac{\pi}{3}\) | \(\cfrac{\pi}{2}\) | \(\cfrac{2\pi}{3}\) | \(\cfrac{3\pi}{4}\) | \(\cfrac{5\pi}{6}\) | \(\pi\) |
|---|---|---|---|---|---|---|---|---|---|
| \(deg\) | \(0^{\circ}\) | \(30^{\circ}\) | \(45^{\circ}\) | \(60^{\circ}\) | \(90^{\circ}\) | \(120^{\circ}\) | \(135^{\circ}\) | \(150^{\circ}\) | \(180^{\circ}\) |
| \(sin\theta\) | \(0=\frac{\sqrt{0}}{2}\) | \(\frac{1}{2}=\frac{\sqrt{1}}{2}\) | \(\cfrac{\sqrt{2}}{2}\) | \(\cfrac{\sqrt{3}}{2}\) | \(1=\cfrac{\sqrt{4}}{2}\) | \(\cfrac{\sqrt{3}}{2}\) | \(\cfrac{\sqrt{2}}{2}\) | \(\cfrac{1}{2}\) | \(0\) |
| \(cos\theta\) | \(1=\frac{\sqrt{4}}{2}\) | \(\frac{\sqrt{3}}{2}\) | \(\cfrac{\sqrt{2}}{2}\) | \(\cfrac{1}{2}=\cfrac{\sqrt{1}}{2}\) | \(0=\cfrac{\sqrt{0}}{2}\) | \(-\cfrac{1}{2}=-\cfrac{\sqrt{1}}{2}\) | \(-\cfrac{\sqrt{2}}{2}\) | \(-\cfrac{\sqrt{3}}{2}\) | \(-1=-\frac{\sqrt{4}}{2}\) |
| \(tan\theta\) | \(0\) | \(\cfrac{\sqrt{3}}{3}\) | \(1\) | \(\sqrt{3}\) | \(\infty\) | \(-\sqrt{3}\) | \(-1\) | \(-\cfrac{\sqrt{3}}{3}\) | \(0\) |
常用结论
- 高频变形公式
\(2sin\theta cos\theta=sin2\theta\);\(2cos^2\theta-1=1-2sin^2\theta=cos2\theta\);
\(asin\theta+bcos\theta=\sqrt{a^2+b^2}\left(\cfrac{a}{\sqrt{a^2+b^2}}sin\theta+\cfrac{b}{\sqrt{a^2+b^2}}cos\theta\right)\)
\(=\sqrt{a^2+b^2}(cos\phi\cdot sin\theta+sin\phi\cdot cos\theta)\)
\(=\sqrt{a^2+b^2}sin(\theta+\phi)\;\;(备注:tan\phi=\cfrac{b}{a})\)
-
再把\(\theta\Longrightarrow (2x+\cfrac{\pi}{3})\)试试看,考查整体思想。同角三角函数基本关系:\(sin^2(2\theta+\cfrac{\pi}{3})+cos^2(2\theta+\cfrac{\pi}{3})=1\),
-
常用的勾股数\(3n,4n,5n(n\in N^*)\);\(5,12,13\);\(7,24,25\);\(8,15,17\);\(9,40,41\);
如已知\(\alpha\)为第二象限角,\(\sin\alpha+\cos\alpha=\cfrac{1}{5}\),则可知,\(\sin\alpha=\cfrac{4}{5}\),\(\cos\alpha=-\cfrac{3}{5}\),
再如已知\(\alpha\)为第二象限角,\(\sin\alpha+\cos\alpha=-\cfrac{1}{5}\),则可知,\(\sin\alpha=\cfrac{3}{5}\),\(\cos\alpha=-\cfrac{4}{5}\),
- 需要我们烂熟于心的三角变形:
\(sin\theta\pm cos\theta=\sqrt{2}sin(\theta\pm\cfrac{\pi}{4})\);\(\sqrt{2}sin\theta\pm \sqrt{2}cos\theta=2sin(\theta\pm\cfrac{\pi}{4})\);
\(\cfrac{\sqrt{3}}{2}sin\theta\pm\cfrac{1}{2}cos\theta=sin(\theta\pm\cfrac{\pi}{6})\);\(\cfrac{1}{2}sin\theta\pm\cfrac{\sqrt{3}}{2}cos\theta=sin(\theta\pm\cfrac{\pi}{3})\);
\(\sqrt{3}sin\theta\pm cos\theta=2sin(\theta\pm\cfrac{\pi}{6})\);\(sin\theta\pm\sqrt{3}cos\theta=2sin(\theta\pm\cfrac{\pi}{3})\);
-
在\(\Delta ABC\)中,已知\(\angle A=\cfrac{\pi}{3}\),求\(sinB+sinC=sinB+sin(\cfrac{2\pi}{3}-B)\);\(sinB\cdot sinC=sinB\cdot sin(\cfrac{2\pi}{3}-B)\);
-
三角函数的单调区间的演示
- 在锐角\(\Delta ABC\)中,\(sinA>cosB\),\(cosA<sinB\)。
证明:由于在锐角\(\Delta ABC\)中,故\(A+B>\cfrac{\pi}{2}\),即\(A>\cfrac{\pi}{2}-B\),此时\(A\in(0,\cfrac{\pi}{2})\),\(\cfrac{\pi}{2}-B\in(0,\cfrac{\pi}{2})\),而函数\(y=sinx\)在\((0,\cfrac{\pi}{2})\)上是单调递增的,故\(sinA>sin(\cfrac{\pi}{2}-B)=cosB\),即\(sinA>cosB\),
同理,函数\(y=cosx\)在\((0,\cfrac{\pi}{2})\)上是单调递减的,故\(cosA<cos(\cfrac{\pi}{2}-B)=sinB\),即\(cosA<sinB\)。
- 在\(\Delta ABC\)中,$A>B\Leftrightarrow sinA>sinB\Leftrightarrow a>b $(利用正弦定理和大角对大边可证明)
在\(\Delta ABC\)中,\(A>B\Leftrightarrow cosA<cosB\)(利用余弦函数的单调性可证明)
- “\(a^2+b^2>c^2\)”是“\(\triangle ABC\)是锐角\(\triangle\)”的必要不充分条件;
“\(a^2+b^2<c^2\)”是“\(\triangle ABC\)是钝角\(\triangle\)”的充分不必要条件;
“\(a^2+b^2=c^2\)”是“\(\triangle ABC\)是\(Rt\triangle\)”的充分不必要条件;
- 求值:\(sin^21^{\circ}+sin^22^{\circ}+sin^23^{\circ}+\cdots+sin^288^{\circ}+sin^289^{\circ}=\)
分析:\(sin^21^{\circ}+sin^289^{\circ}=1\),\(sin^22^{\circ}+sin^288^{\circ}=1\),\(\cdots\),\(sin^244^{\circ}+sin^246^{\circ}=1\),\(sin^245^{\circ}=\cfrac{1}{2}\),
故原式=\(44+\cfrac{1}{2}=44.5\)。
\(cos^21^{\circ}+cos^22^{\circ}+cos^23^{\circ}+\cdots+cos^288^{\circ}+cos^289^{\circ}=44.5\)
\((1+tan22^{\circ})(1+tan23^{\circ})=2\)
5、已知\(tan\alpha=\cfrac{1}{2}\),求\(sin^4\alpha-cos^4\alpha\)的值。
【法1】:方程组法,由\(\left\{\begin{array}{l}{\cfrac{sin\alpha}{cos\alpha}=\cfrac{1}{2}}\\{sin^2\alpha+cos^2\alpha=1}\end{array}\right.\),
解得\(sin^2\alpha=\cfrac{1}{5}\),\(cos^2\alpha=\cfrac{4}{5}\),
代入得到\(sin^4\alpha-cos^4\alpha=-\cfrac{3}{5}\);
【法2】:齐次式法,\(sin^4\alpha-cos^4\alpha=(sin^2\alpha-cos^2\alpha)(sin^2\alpha+cos^2\alpha)=sin^2\alpha-cos^2\alpha\)
\(=-cos2\alpha=-\cfrac{cos^2\alpha-sin^2\alpha}{sin^2\alpha+cos^2\alpha}=\cfrac{1-tan^2\alpha}{1+tan^2\alpha}=-\cfrac{3}{5}\);
【法3】:由\(\cfrac{sin\alpha}{cos\alpha}=\cfrac{1}{2}\),引入比例因子,可设\(sin\alpha=k\),\(cos\alpha=2k(k\neq 0)\),
由\(k^2+(2k)^2=1\),可得\(k^2=\cfrac{1}{5}\),故\(k^4=\cfrac{1}{25}\),
则\(sin^4\alpha-cos^4\alpha=k^4-(2k)^4=-15k^4=-\cfrac{3}{5}\);
6、三角函数章节中的重要不等式:\(\theta\in (0,\cfrac{\pi}{2})\)时,\(sin\theta<\theta<tan\theta\)。
【证法1】:三角函数线法,如图所示为单位圆,则\(sin\theta=MP\),\(tan\theta=AT\),\(\overset{\frown}{AP}=\theta\cdot 1=\theta\)
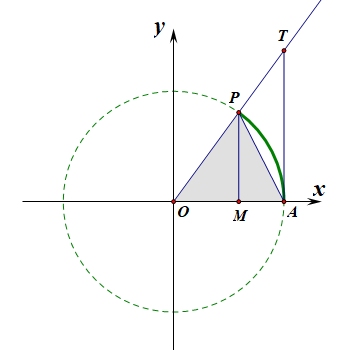
由图可知,\(S_{\Delta OAP}<S_{扇形 OAP}<S_{\Delta OAT}\)
即\(\cfrac{1}{2}\cdot |OA|\cdot MP<\cfrac{1}{2}\cdot \theta \cdot |OA|<\cfrac{1}{2}\cdot |OA|\cdot AT\)
则有\(MP<\theta< AT\),即\(sin\theta<\theta<tan\theta\)。
故\(\theta\in (0,\cfrac{\pi}{2})\)时,\(sin\theta<\theta<tan\theta\)。
【证法2】:构造函数法,如令\(g(x)=sinx-x\),\(x\in (0,\cfrac{\pi}{2})\),
则\(g'(x)=cosx-1\leq 0\)恒成立,故\(g(x)\)在\(x\in (0,\cfrac{\pi}{2})\)上单调递减,
故\(g(x)<g(0)=0\),即\(sinx<x\),同理可证\(x<tanx\),
故\(\theta\in (0,\cfrac{\pi}{2})\)时,\(sin\theta<\theta<tan\theta\)。
7、已知角\(\theta\)是第Ⅲ象限角,求\(\cfrac{\theta}{2}\)所在的象限。
【法1】:计算法,由于角\(\theta\)是第Ⅲ象限角,
则\(2k\pi+\pi<\theta<2k\pi+\cfrac{3\pi}{2}(k\in Z)\),
则\(k\pi+\cfrac{\pi}{2}<\cfrac{\theta}{2}<k\pi+\cfrac{3\pi}{4}(k\in Z)\),以下针对\(k\)分奇偶讨论:
①当\(k=2n,n\in Z\)时,\(2n\pi+\cfrac{\pi}{2}<\cfrac{\theta}{2}<2n\pi+\cfrac{3\pi}{4}(n\in Z)\),故\(\cfrac{\theta}{2}\)是第Ⅱ象限的角;
②当\(k=2n+1,n\in Z\)时,\(2n\pi+\pi+\cfrac{\pi}{2}<\cfrac{\theta}{2}<2n\pi+\pi+\cfrac{3\pi}{4}(n\in Z)\),故\(\cfrac{\theta}{2}\)是第Ⅳ象限的角;
【法2】:八卦图法,有人对上述解法图形化如下:先将每一个象限都二等分,然后每一个小部分都作以标记,如图所示,最后在图中寻找标号为\(3\)的部分,从而找到所在的象限。
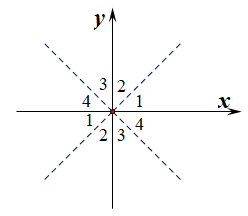
如图,\(\cfrac{\theta}{2}\)是第Ⅱ象限的角或是第Ⅳ象限的角;
8、三角函数中的齐次式
比如:\(\cfrac{a\sin\theta+b\cos\theta}{c\sin\theta+d\cos\theta}\xlongequal[分子分母是sin\theta,cos\theta的一次齐次式]{分子分母同除以cos\theta}\cfrac{a\tan\theta+b}{c\tan\theta+d}\) (\(a,b,c,d\)为常数);
小结:实现了二元\(sin\theta、cos\theta\)向一元\(tan\theta\)的转化;
比如:\(\cfrac{\sin2\theta-\cos^2\theta}{1+\sin^2\theta}=\cfrac{2sin\theta cos\theta-cos^2\theta}{2sin^2\theta+cos^2\theta}\xlongequal[分子分母是sin\theta,cos\theta的二次齐次式]{分子分母同除以cos^2\theta}\cfrac{2tan\theta-1}{2tan^2\theta+1}\)
小结:实现了二元\(sin\theta、cos\theta\)向一元\(tan\theta\)的转化;
再比如:\(a\sin2\theta+b\cos2\theta=\cfrac{a\sin2\theta+b\cos2\theta}{sin^2\theta+cos^2\theta}=\cfrac{a\tan\theta+b-b\tan^2\theta}{tan^2\theta+1}\),
其余留作思考:\(\sin2\theta\), \(\cos2\theta\),\(1+\sin2\theta\), \(2-\cos2\theta\),\(3\sin2\theta-2\cos2\theta\) 等等
9、三角公式的扩展:
\(1+cos\theta=2cos^2\cfrac{\theta}{2}\);\(1-cos\theta=2sin^2\cfrac{\theta}{2}\)
\(1+sin\theta=(sin\cfrac{\theta}{2}+cos\cfrac{\theta}{2})^2\);\(1-sin\theta=(sin\cfrac{\theta}{2}-cos\cfrac{\theta}{2})^2\);
\(1+sin\theta+cos\theta=1+cos\theta+sin\theta=2cos^2\cfrac{\theta}{2}+2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}=2cos\cfrac{\theta}{2}(cos\cfrac{\theta}{2}+sin\cfrac{\theta}{2})\)
\(1+sin\theta-cos\theta=1-cos\theta+sin\theta=2sin^2\cfrac{\theta}{2}+2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}=2sin\cfrac{\theta}{2}(cos\cfrac{\theta}{2}+sin\cfrac{\theta}{2})\)
\(1-sin\theta+cos\theta=1+cos\theta-sin\theta=2cos^2\cfrac{\theta}{2}-2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}=2cos\cfrac{\theta}{2}(cos\cfrac{\theta}{2}-sin\cfrac{\theta}{2})\)
\(1-sin\theta-cos\theta=1-cos\theta-sin\theta=2sin^2\cfrac{\theta}{2}-2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}=2sin\cfrac{\theta}{2}(sin\cfrac{\theta}{2}-cos\cfrac{\theta}{2})\)
在\(\Delta ABC\)中,\(sin(A+B)=sinC\);\(cos(A+B)=-cosC\);\(tan(A+B)=-tanC\);
\(sin\cfrac{A+B}{2}=cos\cfrac{C}{2}\);\(cos\cfrac{A+B}{2}=sin\cfrac{C}{2}\);
10、平方关系的应用
\(sin\alpha+cos\alpha\),\(sin\alpha-cos\alpha\),\(sin\alpha\cdot cos\alpha\),知一求二意味着知道其中的一个,就能表达另外的两个式子;方程思想;
如求函数\(h(x)=sinx\pm cosx\pm sinx\cdot cosx\)类型的值域;
求函数\(f(x)=sinx+cosx+sinx\cdot cosx\)的值域;
令\(sinx+cosx=t\),则\(t=\sqrt{2}sin(x+\cfrac{\pi}{4})\),则\(t\in [-\sqrt{2},\sqrt{2}]\);
给\(sinx+cosx=t\)两边平方,整理得到\(sinx\cdot cosx=\cfrac{t^2-1}{2}\),
故原函数\(f(x)=g(t)=t+\cfrac{t^2-1}{2}\),\(t\in [-\sqrt{2},\sqrt{2}]\);
转化划归为二次函数在给定区间上的值域问题;
再比如\(g(x)=\cfrac{2sinx cosx}{sinx+cosx},x\in [0,\cfrac{\pi}{2}]\)的值域;

 总结梳理三角函数知识点。
总结梳理三角函数知识点。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号