数列习题
解析:令\(a_n=3n-63\leq 0\),则\(n\leq 21\),
故数列\(\{|a_n|\}\)的通项公式为\(|a_n|= \begin{cases}63-3n &n\leq 21 \\ 3n-63 &n\ge22 \end{cases}\)
[备注:由于数列的通项公式是分段函数,所以其前\(n\)项和自然也应该用分段函数来表达刻画]
\(1^。\) 当\(n\leq 21\),\(T_n=|a_1|+|a_2|+\cdots+|a_n|\)
\(=-a_1-a_2-\cdots-a_n\)
\(=-\cfrac{(a_1+a_n)\times n}{2}\)
\(=-\cfrac{[-60+(3n-63)]\times n}{2}\)
\(=-\cfrac{3n^2-123n}{2}=\cfrac{123n-3n^2}{2}\).
\(2^。\) 当\(n\ge 22\),\(T_n=|a_1|+|a_2|+\cdots+|a_n|\)
\(=-a_1-a_2-\cdots-a_{21}+a_{22}+\cdots+a_n\)
\(=(a_1+a_2+\cdots+a_{21}+a_{22}+\cdots+a_n)-2(a_1+a_2+\cdots+a_{21})\)
\(=S_n-2S_{21}\)\(=\cfrac{[-60+(3n-63)]n}{2}-2\times\cfrac{[(3\times 1-63)+(3\times 21-63)]\times 21}{2}\)
$=\cfrac{3n^2-123n}{2}+1260 $.
故数列\(\{|a_n|\}\)的前\(n\)项和\(T_n=\begin{cases}\cfrac{123n-3n^2}{2} &n\leq 21 \\ \cfrac{3n^2-123n}{2}+1260 &n\ge 22\end{cases}\)
(1)求\(a_4\)的值。
分析:(1)简单的数字运算,不过你得注意必须用\(S_n\)的定义式,
即\(S_n=a_1+a_2+\cdots+a_n\),
不能用等差或等比的前\(n\)项和公式,因为题目没有告诉你数列的性质。
当\(n=2\)时\(4S_4+5S_2=8S_3+S_1\),
即\(4(a_1+a_2+a_3+a_4)+5(a_1+a_2)=8(a_1+a_2+a_3)+a_1\),
将已知条件代入,解得\(a_4=\cfrac{7}{8}\)。
(2)证明:\(\{a_{n+1}-\cfrac{1}{2}a_n\}\)为等比数列。
分析:题目告诉的条件是关于\(S_n\)类的,而要求解的是关于\(a_n\)类的,
所以变形的方向肯定是要消去\(S_n\)类的,全部转化为\(a_n\)类的。
但是这里有了两个变形思路和变形方向:纵向变形和横向变形,
思路一:纵向变形,\(n\ge 2\)时,\(4S_{n+2}+5S_n=8S_{n+1}+S_{n-1}\).
仿此构造如下式子
\(n\ge 1\)时,\(4S_{n+3}+5S_{n+1}=8S_{n+2}+S_n\).两式相减得到
\(n\ge 2\)时,\(4a_{n+3}+5a_{n+1}=8a_{n+2}+a_n\). 到此思路受阻,
打住。为什么?
我们证明到最后肯定会得到
\((a_{n+2}-\cfrac{1}{2}a_{n+1})=k(a_{n+1}-\cfrac{1}{2}a_n)\)
或者\((a_{n+1}-\cfrac{1}{2}a_{n})=k(a_n-\cfrac{1}{2}a_{n-1})\),
这两个式子都只是涉及到\(a_n\)类的三项,而我们思路一的涉及到了四项,
所以变形的思路受阻了,得到启示,我们变化如下,
思路二:横向变形,由题目结论的指向作用知道,
不是纵向构造式子做差,应该是就此式子横向做变形,
\(n\ge 2\)时,\(4S_{n+2}+5S_n=8S_{n+1}+S_{n-1}\),
即就是\((4S_{n+2}-4S_{n+1})=(4S_{n+1}-4S_n)-(S_n-S_{n-1})\),
得到\(4a_{n+2}=4a_{n+1}-a_n\),变形得到,
\(a_{n+2}=a_{n+1}-\cfrac{1}{4}a_n\),
比照题目结论,尝试给两边同时加上\(-\cfrac{1}{2}a_{n+1}\),整理得到
当\(n\ge 2\)时,\((a_{n+2}-\cfrac{1}{2}a_{n+1})=\cfrac{1}{2}(a_{n+1}-\cfrac{1}{2}a_n)\),
这样基本的等比数列的大样有了,接下来是细节的验证,
其一验证\((a_3-\cfrac{1}{2}a_2)=\cfrac{1}{2}(a_2-\cfrac{1}{2}a_1)\),
其二还得说明\(a_2-\cfrac{1}{2}a_1\ne 0\),
才能说明这是个等比数列。
是否将\((a_{n+2}-\cfrac{1}{2}a_{n+1})=\cfrac{1}{2}(a_{n+1}-\cfrac{1}{2}a_n)\)改写为分式形式,
不是必要的。
(3)求数列\(\{a_n\}\)的通项公式。
分析:由第二问知道,\(\{a_{n+1}-\cfrac{1}{2}a_n\}\)为首项为1,公比为\(\cfrac{1}{2}\)的等比数列,
故\(a_{n+1}-\cfrac{1}{2}a_n=1\cdot(\cfrac{1}{2})^{n-1}\)
即\(a_{n+1}=\cfrac{1}{2}a_n+1\cdot(\cfrac{1}{2})^{n-1}\),两边同乘以\(2^{n+1}\)得到,
所以\(2^{n+1}\cdot a_{n+1}-2^n\cdot a_n=4\),
数列\(\{2^n\cdot a_n\}\)是首项为\(2^1\cdot a_1=2\),公差为4的等差数列,
所以\(2^n\cdot a_n=2+4(n-1)=4n-2\),
故\(a_n=\cfrac{2n-1}{2^{n-1}}\)。
解析:由已知可得\(S_n=1-(-\cfrac{1}{3})^n=1-(-1)^n(\cfrac{1}{3})^n\)
当\(n\)为奇数时,\(S_n=1+(\cfrac{1}{3})^n\),则\(S_n\searrow\),\(1< S_n\leq \cfrac{4}{3}\);
当\(n\)为偶数时,\(S_n=1-(\cfrac{1}{3})^n\),则\(S_n\nearrow\),\(\cfrac{8}{9}\leq S_n<1\);
故\(\cfrac{8}{9}\leq S_n \leq \cfrac{4}{3}\)(在区间内是离散取值的,不是连续取值,我们其实关注的是两个端点值)
又\(A\leq S_n-\cfrac{1}{S_n}\leq B\);
\(f(x)=x-\cfrac{1}{x}\)在区间\((0,+\infty)\)上单调递增,则在区间\([\cfrac{8}{9},\cfrac{4}{3}]\)上也递增,故可得
\((S_n-\cfrac{1}{S_n})_{min}=A=\cfrac{8}{9}-\cfrac{9}{8}=-\cfrac{17}{72}\);\((S_n-\cfrac{1}{S_n})_{max}=B=\cfrac{4}{3}-\cfrac{3}{4}=\cfrac{7}{12}\)
所以\(B-A\)的最小值为\(\cfrac{7}{12}-(-\cfrac{17}{72})=\cfrac{59}{72}\)。
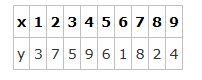
数列\(\{x_n\}\)满足:\(x_1=1\),且对于任意的\(n\in N_*\),点\((x_n,x_{n+1})\)都在函数\(y=f(x)\)的图像上,
则\(x_1+x_2+\cdots+x_{2015}=?\)
分析:这是一个很新颖的数列题目,但是和函数的列表法紧密结合,要顺利解答还需要一定的数学素养。
由题目可知\(y=f(x),x_{n+1}=f(x_n),x_1=1\),
则有\(x_2=f(x_1)=f(1)=3\);\(x_3=f(x_2)=f(3)=5\);\(x_4=f(x_3)=f(5)=6\);
\(x_5=f(x_4)=f(6)=1\);\(\cdots,T=4\);
\(\sum\limits_{k=1}^{2015}{x_k}=503(x_1+x_2+x_3+x_4)+(x_1+x_2+x_3)=503\times 15+9=7554\)
法1:【迭代递推】
\(a_1=f(2^1)=2\),即\(f(2)=2\),
\(a_n=f(2^n)=f(2\cdot2^{n-1})=2f(2^{n-1})+2^{n-1}f(2)\)
\(=2^1\cdot f(2^{n-1})+2^n\cdot 1=2[2f(2^{n-2})+2^{n-2}f(2)]+2^n\cdot 1\)
\(=2^2\cdot f(2^{n-2})+2^n\cdot 2\)
\(=2^3\cdot f(2^{n-3})+2^n\cdot 3\)
\(=2^4\cdot f(2^{n-4})+2^n\cdot 4\)
\(=2^{n-1}\cdot f(2^1)+2^n \cdot (n-1)=n\cdot 2^n\);
法2:【赋值法】
由题目\(a_n=f(2^n)\)可知,\(a_{n+1}=f(2^{n+1})\),且\(a_1=f(2)=2\)
由于对任意的\(x,y\in R\)都有\(f(xy)\)\(=xf(y)\)\(+yf(x)\)成立,
令\(x=2^n\),\(y=2\),则有\(f(2^{n+1})=f(2^n\cdot 2)=2^nf(2)+2f(2^n)\),
即\(a_{n+1}=2a_n+2\times 2^n\),即\(a_{n+1}=2a_n+2^{n+1}\),
接下来两边同时除以\(2^{n+1}\),得到
\(\cfrac{a_{n+1}}{2^{n+1}}=\cfrac{a_{n}}{2^{n}}+1\)
则数列\(\{\cfrac{a_n}{2^n}\}\)是首项为\(1\),公差为\(1\)的等差数列,
则有\(\cfrac{a_n}{2^n}=1+(n-1)\times 1=n\),
即所求通项公式为\(a_n=n\cdot 2^n\)。
法1:可以计算出数列的前有限项,归纳猜想得到通项公式从而求解;
由题目可知\(f_1(x)=\cfrac{2}{1+x},f_{n+1}(x)=f_1(f_n(x))\),
将\(f_n(x)\)代入\(f_1(x)\)得到,\(f_{n+1}(x)=\cfrac{2}{1+f_n(x)}\),
用此式依次计算得到:
\(f_1(x)=\cfrac{2}{1+x},f_1(0)=2,a_1=\cfrac{f_1(0)-1}{f_1(0)+1}=\cfrac{1}{4}\);
\(f_2(x)=\cfrac{2(1+x)}{3+x},f_2(0)=\cfrac{2}{3},a_2=\cfrac{f_2(0)-1}{f_2(0)+1}=-\cfrac{1}{8}\);
\(f_3(x)=\cfrac{2(3+x)}{5+3x},f_3(0)=\cfrac{6}{5},a_3=\cfrac{f_3(0)-1}{f_3(0)+1}=\cfrac{1}{16},\cdots\);
由此猜想数列\(\{a_n\}\)是首项为\(\cfrac{1}{4}\),公比为\(-\cfrac{1}{2}\)的等比数列,
通项公式为\(a_n=\cfrac{1}{4}\cdot(-\cfrac{1}{2})^{n-1}\),
则\(a_{2017}=\cfrac{1}{4}\cdot(-\cfrac{1}{2})^{2017-1}=\cfrac{1}{2^{2018}}\).
法2:由上式得到启发,我们可以直接计算如下:
\(\cfrac{a_{n+1}}{a_n}=\cfrac{\cfrac{f_{n+1}(0)-1}{f_{n+1}(0)+2}}{\cfrac{f_n(0)-1}{f_n(0)+2}}=\cfrac{\cfrac{f_1(f_n(0))-1}{f_1(f_n(0))+2}}{\cfrac{f_n(0)-1}{f_n(0)+2}}\)
\(=\cfrac{\cfrac{\frac{2}{1+f_n(0)}-1}{\frac{2}{1+f_n(0)}+2}}{\cfrac{f_n(0)-1}{f_n(0)+2}}=\cfrac{\cfrac{1-f_n(0)}{2(f_n(0)+2)}}{\cfrac{f_n(0)-1}{f_n(0)+2}} =-\cfrac{1}{2}\),
即\(q=-\cfrac{1}{2}\),再计算\(a_1=\cfrac{f_1(0)-1}{f_1(0)+1}=\cfrac{1}{4}\);
故数列\(\{a_n\}\)是首项为\(\cfrac{1}{4}\),公比为\(-\cfrac{1}{2}\)的等比数列,
通项公式为\(a_n=\cfrac{1}{4}\cdot(-\cfrac{1}{2})^{n-1}\),则\(a_{2017}=\cfrac{1}{4}\cdot(-\cfrac{1}{2})^{2017-1}=\cfrac{1}{2^{2018}}\).
分析:由\(S_n=pn^2-2n,n\in N^*\)[常数项为零的二次函数]可知,数列\(\{a_n\}\)必为等差数列,
由题目可知\(b_2-b_1=2\),即\(\cfrac{a_1+2a_2}{3}-a_1=2\),推出\(a_2-a_1=3\),则数列\(\{a_n\}\)的公差\(d=3\),
再由\(S_n=\cfrac{d}{2}n^2+(a_1-\cfrac{d}{2})=pn^2-2n\)得到\(a_1-\cfrac{d}{2}=-2\),解得\(a_1=-\cfrac{1}{2}\),
故通项公式\(a_n=-\cfrac{1}{2}+(n-1)3=3n - \cfrac{7}{2}\).
法1:常规方法,先求得\(n\ge 2\)时,\(a_{n+1}=3a_n+2\),
再变形为\(a_{n+1}+1=3(a_n+1)\),
再验证,当\(n=1\)时,\(a_2=8\),\(a_2+1=9=3(a_1+1)\),满足上式;
故数列\(\{a_n+1\}\)是首项为3,公比为3的等比数列,
故\(a_n+1=3\cdot3^{n-1}=3^n\),所以\(a_n=3^n-1\),
从而求得\(S_n=\cfrac{3^{n+1}}{2}-n-\cfrac{3}{2}\).
法2:将\(a_{n+1}=S_{n+1}-S_n\)代入\(a_{n+1}=2S_n+2n+2\),整理得到\(S_{n+1}=3S_n+2n+2\),
再变形为\(S_{n+1}+p(n+1)+q=3(S_n+pn+q)(p、q为常数)\),可解得\(p=1,q=\cfrac{3}{2}\),
即\(S_{n+1}+(n+1)+\cfrac{3}{2}=3(S_n+n+\cfrac{3}{2})\),
则数列\(\{S_n+n+\cfrac{3}{2}\}\)是首项为\(a_1+1+\cfrac{3}{2}=\cfrac{9}{2}\),公比为3的等比数列;
故\(S_n+n+\cfrac{3}{2}=\cfrac{9}{2}\cdot 3^{n-1}\),整理得到\(S_n=\cfrac{3^{n+1}}{2}-n-\cfrac{3}{2}\).
分析:对已知式子\(a_9\cdot a_{2008}=\cfrac{1}{4}\)两边同时取以\(2\)为底的对数,
得到\(log_2^{a_9\cdot a_{2008}}=log_2^{\frac{1}{4}}\),
即\(log_2^{a_9}+\cdot log_2^{a_{2008}}=-2\),也就是\(b_9+b_{2008}=-2=b_1+b_{2016}\),
故\(b_1+b_2+\cdots +b_{2016}=\cfrac{b_1+b_{2016}}{2}\times 2016=-2016\).
法1:提取出的等比数列的首项是\(a_1=2\),第二项是\(a_{k_2}=\cfrac{2k_2+4}{3}\),则公比\(q=\cfrac{2k_2+4}{2\times 3}\),
第三项是\(a_{k_3}=\cfrac{2k_3+4}{3}\),由等比数列可知\((a_{k_2})^2=a_1a_{k_3}\),即\((\cfrac{2k_2+4}{3})^2=2\cfrac{2k_3+4}{3}\),
化简得到\(k_2^2+4k_2=3k_3+2\),要是公比最小,则需要\(k_2\)尽可能的小,为此,将\(k_3=3\)开始尝试,
如果能解得\(k_2\in N^* 且1<k_2<k_3\),则\(k_2\)必是满足题意的,
当\(k_3=3,4,\cdots,9\)都不能满足\(k_2\in N^*\),当\(k_3=10\)时,解得\(k_2=4\),
代入公比\(q=\cfrac{2\times 4 +4}{2\times 3}=2\).
法2:待补充
分析:和式用减,
当\(n \ge 1\)时,\(2^1a_1+2^2a_2+2^3a_3+\dots+2^na_n = n ①\),
当\(n \ge 2\)时,\(2^1a_1+2^2a_2+2^3a_3+\dots+2^{n-1}a_{n-1} = n-1②\),两式相减得到
当\(n \ge 2\)时,\(2^na_n=1\),即就是\(a_n=\cfrac{1}{2^n}=(\cfrac{1}{2})^n\),
再验证,当\(n=1\)时,由已知式子可知\(a_1=\cfrac{1}{2}\),满足上式,故数列\(\{a_n\}\)的通项公式为\(a_n=(\cfrac{1}{2})^n\) .
分析:积式用商
当\(n \ge 1\)时,\(b_1\cdot b_2 \cdot b_3 \cdots b_n= 2^{S_n} ①\),
当\(n \ge 2\)时,\(b_1\cdot b_2 \cdot b_3 \cdots b_{n-1}= 2^{S_{n-1}}②\),两式相除得到
当\(n \ge 2\)时,\(b_n=2^{S_n-S_{n-1}}=2^{a_n}\),即\(b_n=2^{a_n}=2^n\),
再验证,当\(n=1\)时,由已知式子可知\(b_1=2^{S_1}=2^{a_1}=2\),满足上式,故数列\(\{b_n\}\)的通项公式为\(b_n=2^n\).
(2)若\(\lambda b_n>a_n\)对\(n\in N^*\)都成立,求实数\(\lambda\)的取值范围。
分析:当变形为\(\lambda>\cfrac{a_n}{b_n}\),若此时看不到解题方向,可以这样联系,若\(\lambda>f(n)\)恒成立呢?
若\(\lambda>f(x)\)恒成立呢?这样就容易想到需要判断\(\cfrac{a_n}{b_n}\)的单调性:
思路一作商作差法;思路二借助函数的单调性;思路三借助不同函数的增长速度的不同
思路1:变形为\(\lambda>\cfrac{a_n}{b_n}\),即\(\lambda>\cfrac{n}{2^n}\),设\(c_n=\cfrac{n}{2^n}\),
则\(\cfrac{c_{n+1}}{c_n}=\cfrac{\cfrac{n+1}{2^{n+1}}}{\cfrac{n}{2^n}}=\cfrac{n+1}{2n}\leq 1\),
故\(c_{n+1}\leq c_n\),当且仅当\(n=1\)时等号成立,故数列\(\{c_n\}\)单调递减,
则有\((c_n)_{max}=\cfrac{1}{2}\),即\(\lambda>\cfrac{1}{2}\),故实数\(\lambda\)的取值范围为\(\lambda>\cfrac{1}{2}\)。
思路2:令\(f(x)=\cfrac{x}{2^x}\),可以看看这个课件
用常用的导数方法,可以求得函数在\((0,+\infty)\)上的单调性,
具体是在\((0,log_2^e]\)上单调递增,在\([log_2^e,+\infty)\)上单调递减,
又\(1<log_2^e<2\),故借助函数\(f(x)\)的单调性计算得到,\(a_1=\cfrac{1}{2}=a_2<a_3<a_4<\cdots<a_n<\cdots\),
故数列\(c_n=\cfrac{n}{2^n}\)的最大值为\(\cfrac{1}{2}\).
思路3:借助幂函数\(y=x\)的增长速度比指数函数\(y=2^x\)的慢,故\(f(x)=\cfrac{x}{2^x}\)从某个\(x_0\)开始向右,
一定是单调递减的,但是前面的这一段还是不太好判断。
分析:要求数列\(\{b_n\}\)的前\(n\)项和\(T_n\),一般都是先需要求出通项公式\(b_n\),
注意到数列的给定条件实质是\(c_{n+1}-c_n=f(n)\)的形式,故可以考虑用累加法。
由题目条件,\(\cfrac{1}{b_{n+1}}-\cfrac{1}{b_n}=2n+3\),
由上式衍生得到以下表达式:
当\(n\ge 2\)时,
以上\(n-1\)个式子累加,得到当\(n\ge 2\)时,
\(\cfrac{1}{b_n}-\cfrac{1}{b_1}=2[(n-1)+(n-2)+\cdots+2+1]+3(n-1)\)
\(=2\cfrac{(1+n-1)(n-1)}{2}+3(n-1)=n^2+2n-3\);
故\(\cfrac{1}{b_n}=n(n+2)\),再验证\(n=1\)对上式也成立,
则通项公式\(b_n=\cfrac{1}{n(n+2)}=\cfrac{1}{2}(\cfrac{1}{n}-\cfrac{1}{n+2})(n\in N^*)\)
故\(T_n=\cfrac{1}{2}[(1-\cfrac{1}{3})+(\cfrac{1}{2}-\cfrac{1}{4})+\cdots+(\cfrac{1}{n}-\cfrac{1}{n+2})]\)
\(=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{n+1}-\cfrac{1}{n+2})\)
\(=\cfrac{3n^3+5n}{4(n+1)(n+2)}\);
当然,在计算\(b_n\)时,还可以采用这样的变形技巧:
当\(n\ge 2\)时,
\(\cfrac{1}{b_n}=(\cfrac{1}{b_n}-\cfrac{1}{b_{n-1}})+(\cfrac{1}{b_{n-1}}-\cfrac{1}{b_{n-2}})+\cdots+(\cfrac{1}{b_2}-\cfrac{1}{b_1})+\cfrac{1}{b_1}\)
\(=a_{n-1}+a_{n-2}+\cdots+a_1+\cfrac{1}{b_1}\)
\(=\cfrac{1}{2}(n-1)(2n+6)=n(n+2)\),
再验证\(n=1\)对上式也成立,
故\(b_n=\cfrac{1}{n(n+2)}=\cfrac{1}{2}(\cfrac{1}{n}-\cfrac{1}{n+2})(n\in N^*)\)。
分析:由题目\(S_5=75=5a_1+10d\),则有\(a_1+2d=15\),
又由于\((1-x)^m\)的展开式中\(x^2\)项的系数为\(C_m^2\),
数列\(\{a_n\}\)的第三项\(a_2=a_1+2d=15\),
故\(C_m^2=15\),解得\(m=6\)(\(m=-5\)舍去);
法1:以少御多,将无限项转化为有限项,再由多转少,这样便于思考和运算;可以假定\(n=4\),然后代入验证,选\(C\).
法2:写出新数列的通项公式\(a_k=\cfrac{1}{k}\cdot \cfrac{n}{2}\),注意通项公式不是\(a_n=\cfrac{1}{n}\cdot \cfrac{n}{2}\),
这样求和的数列的通项公式就是
\(k\ge 2\),\(a_{k-1}a_k=\cfrac{n^2}{4}\cfrac{1}{(k-1)k}=\cfrac{n^2}{4}(\cfrac{1}{k-1}-\cfrac{1}{k})\)
故\(a_1a_2+a_2a_3+a_3a_4+\cdots+a_{n-1}a_n\)
\(=\cfrac{n^2}{4}[(1-\cfrac{1}{2})+(\cfrac{1}{2}-\cfrac{1}{3})+(\cfrac{1}{3}-\cfrac{1}{4})+\cdots+(\cfrac{1}{k-1}-\cfrac{1}{k})]\)
\(=\cfrac{n^2}{4}(1-\cfrac{1}{n})=\cfrac{n(n-1)}{4}\).
分析:本题目先由\(S_n\)求得\(b_n\),再求得\(c_n\),依据\(c_n\)是等比数列,则其通项公式可以写成指数型函数得到方程,从而求得\(a、t\);
解析:本题目先由\(S_{n+1}=tS_n+a\),两边同时加上常数\(\cfrac{a}{t-1}\),得到\(S_{n+1}+\cfrac{a}{t-1}=t(S_n+\cfrac{a}{t-1})\),
则数列\(\{S_n+\cfrac{a}{t-1}\}\)是首项为\(S_1+\cfrac{a}{t-1}=\cfrac{at}{t-1}\),公比为\(t\)的等比数列,
故\(S_n+\cfrac{a}{t-1}=\cfrac{at}{t-1}\cdot t^{n-1}\),
即\(S_n=\cfrac{at}{t-1}\cdot t^{n-1}-\cfrac{a}{t-1}=\cfrac{a}{t-1}\cdot t^n-\cfrac{a}{t-1}\),
\(b_n=S_n+1=\cfrac{a}{t-1}\cdot t^n-\cfrac{a}{t-1}+1\)
故\(c_n=2+b_1+b_2+\cdots+b_n=2+n-\cfrac{a}{t-1}n+\cfrac{a}{t-1}(t+t^2+\cdots+t^n)\)
\(=2+n-\cfrac{a}{t-1}n+\cfrac{a}{t-1}\cfrac{t(t^n-1)}{t-1}\)
\(=n(1-\cfrac{a}{t-1})+(2-\cfrac{at}{(t-1)^2})+\cfrac{at^{n+1}}{(t-1)^2}\)
由于数列\(\{c_n\}\)为等比数列,故其通项公式应该是指数型函数,其他项是\(0\),故得到
\(\begin{cases} &1-\cfrac{a}{t-1}=0\\&2-\cfrac{at}{(t-1)^2}=0\end{cases}\),解得\(a=1,t=2\),故所求的数对为\((1,2)\)。
【备注】已知等比数列的前\(n\)项和\(S_n=r\cdot 2^n-1\),求\(r\)的值。
分析:由于等比数列的前\(n\)项和\(S_n=\cfrac{a(1-q^n)}{1-q}=\cfrac{a}{1-q}\times(1-q^n)\),如果令\(\cfrac{a}{1-q}=-c\),则等比数列的前\(n\)项和\(S_n=cq^n-c\).由此可得,题目中的\(r=1\).
分析:当\(n \ge 1\)时,\(2^1a_1+2^2a_2+2^3a_3+\dots+2^na_n = n ①\),
当\(n \ge 2\)时,\(2^1a_1+2^2a_2+2^3a_3+\dots+2^{n-1}a_{n-1} = n-1②\),两式相减得到
当\(n \ge 2\)时,\(2^na_n=1\),即就是\(a_n=\cfrac{1}{2^n}=(\cfrac{1}{2})^n=2^{-n}\),
再验证,当\(n=1\)时,由已知式子可知\(a_1=\cfrac{1}{2}\),满足上式,
故数列\(\{a_n\}\)的通项公式为\(a_n=(\cfrac{1}{2})^n\) .
故\(\cfrac{1}{log_2^{\;a_n}\cdot log_2^{\;a_{n+1}}}\)
\(=\cfrac{1}{log_2^{\;2^{-n}}\cdot log_2^{\;2^{-n-1}}}\)
\(=\cfrac{1}{n(n+1)}=\cfrac{1}{n}-\cfrac{1}{n+1}\);
故\(S_n=1-\cfrac{1}{n+1}=\cfrac{n}{n+1}\)
故\(S_1\cdot S_2\cdot S_3\cdots S_{10}=\cfrac{1}{2}\times \cfrac{2}{3}\times \cfrac{3}{4}\times \cdots \times \cfrac{10}{11}=\cfrac{1}{11}\).
(1)若\(a_3+b_3=5\),求\(\{b_n\}\)的通项公式。
分析:设等差数列的公差为\(d\),等比数列的公比为\(q\),则由题目可知
\(\begin{cases}-1+d+1\cdot q=2\\-1+2d+1\cdot q^2=5\end{cases}\),即\(\begin{cases}d+ q=3\\2d+ q^2=6\end{cases}\),
解得\(q^2-2q=0\),故\(q=2\)或\(q=0\)(舍去),
故等比数列\(\{b_n\}\)的通项公式为\(b_n=2^{n-1}\)。
(2)若\(T_3=21\),求\(S_3\)。
分析:由于\(b_1=1,T_3=21\),故\(1+q+q^2=21\),解得\(q=-5\)或\(q=4\);
当\(q=-5\)时,由\(a_2+b_2=2\)得到\(d=8\),此时\(S_3=-1+7+15=21\);
当\(q=4\)时,由\(a_2+b_2=2\)得到\(d=-1\),此时\(S_3=-1-2-3=-6\);
分析:由\(a_1+2d=3\)和\(4a_1+6d=10\),容易计算出\(a_n=n\),
故\(S_n=\cfrac{n(n+1)}{2}\),则有\(\cfrac{1}{S_n}=\cfrac{2}{n(n+1)}=2(\cfrac{1}{n}-\cfrac{1}{n+1})\),
故\(\sum\limits_{k=1}^n {\cfrac{1}{S_k}}=2[(1-\cfrac{1}{2})+(\cfrac{1}{2}-\cfrac{1}{3})+\cdots +(\cfrac{1}{n}-\cfrac{1}{n+1})]=2(1-\cfrac{1}{n+1})=\cfrac{2n}{n+1}\)。
(1)求数列\(\{a_n\}\)的通项公式。
分析:本问比较简单,解方程组得到\(a_1=-2,q=-2\),
故\(\{a_n\}\)的通项公式\(a_n=(-2)^n\)。
(2)求\(S_n\),并判断\(S_{n+1},S_n,S_{n+2}\)是否成等差数列。
分析:先求解\(S_n=\cfrac{a_1(1-q^n)}{1-q}=-\cfrac{2}{3}+(-1)^n\cfrac{2^{n+1}}{3}\)。
这一步也不是很难,不过你得意识到,\(S_n\)是个关于自变量\(n\)的函数,故有此我们应该能写出\(S_{n+1}\),\(S_{n+2}\)
至于等差数列的判断,我们依据等差中项法判断即可,即验证\(S_{n+2}+S_{n+1}\)是否等于\(2S_n\)。
判断如下:\(S_{n+2}+S_{n+1}=-\cfrac{4}{3}+(-1)^n\cfrac{2^{n+3}-2^{n+2}}{3}\)
\(=2[-\cfrac{2}{3}+(-1)^n\cfrac{2^{n+1}}{3}]=2S_n\),
故\(S_{n+1},S_n,S_{n+2}\)成等差数列。
(1)求数列\(\{a_n\}\)的通项公式。
分析:本题是利用\(a_n\)和\(S_n\)的关系解题,或者是利用“退一法”解题。
由\(n\ge 1,a_1+3a_2+\cdots+(2n-1)a_n=2n(1)\)得到,\(n\ge 2,a_1+3a_2+\cdots+(2n-3)a_{n-1}=2(n-1)(2)\)
两式相减得到\(n\ge 2,(2n-1)a_n=2\),从而得到\(a_n=\cfrac{2}{2n-1}(n\ge 2)\),
接下来验证\(n=1\)是否满足。当\(n=1\)时,\(a_1=2=\cfrac{2}{2\times 1-1}\),满足上式,
故数列\(\{a_n\}\)的通项公式为\(a_n=\cfrac{2}{2n-1}(n\in N^*)\).
(2)求数列\(\{\cfrac{a_n}{2n+1}\}\)的前\(n\)项和\(S_n\)。
分析:结合第一问,数列\(\cfrac{a_n}{2n+1}=\cfrac{2}{(2n-1)(2n+1)}\)
\(=\cfrac{1}{2n-1}-\cfrac{1}{2n+1}\)
故数列的前\(n\)项和
\(S_n=(\cfrac{1}{2\times1-1}-\cfrac{1}{2\times 1+1})+(\cfrac{1}{2\times 2 -1}-\cfrac{1}{2\times 2+1})+\cdots\)\(+(\cfrac{1}{2n-1}-\cfrac{1}{2n+1})\)
\(=1-\cfrac{1}{2n+1}\)
\(=\cfrac{2n}{2n+1}\)。
法1:函数法,\(a_1=30\),由\(8S_6=9S_3\)得到\(q=\cfrac{1}{2}\),
故\(a_n=30\cdot(\cfrac{1}{2})^{n-1}\),\(T_n=a_1\cdot a_2\cdots a_n\)
\(=30\cdot[30\cdot(\cfrac{1}{2})]\cdots [30\cdot(\cfrac{1}{2})^{n-1}]\)
\(=30^n\cdot (\cfrac{1}{2})^{1+2+\cdots+(n-1)}=30^n\cdot (\cfrac{1}{2})^{\frac{n(n-1)}{2}}\),
题目到此,思路受阻。
法2:\(a_1=30\),由\(8S_6=9S_3\)得到\(q=\cfrac{1}{2}\),故\(a_n=30\cdot(\cfrac{1}{2})^{n-1}\),
由于\(T_n\)为乘积式,故使得\(T_n\)取得最大值时,必有\(a_n\ge 1\),
由此得到\(n\leq 5\)。故\(n_{max}=5\)。
法1:函数法,容易求得\(a_1=8,q=\cfrac{1}{2}\),则\(a_n=8\cdot(\cfrac{1}{2})^{n-1}\);
故\(T_n=a_1\cdot a_2\cdot a_3\cdots a_n=8^n\cdot (\cfrac{1}{2})^{\frac{n(n-1)}{2}}\)
\(=2^{\frac{-n^2+7n}{2}}=2^{\frac{-(n-\frac{7}{2})^2+\frac{49}{4}}{2}}\),
故当\(n=3或4\)时,\(T_n\)有最大值,\((T_n)_{max}=2^6=64\);
法2:仿上法2,使得\(T_n\)取得最大值时,必有\(a_n\ge 1\),由此得到\(n\leq 4\)。
计算得到\(a_1=8\),\(a_2=4\),\(a_3=2\),\(a_4=1\),\(a_5=\cfrac{1}{2}\),
故\(T_n\leq T_4=a_1a_2a_3a_4=64\);
解后反思:
1、等差数列中由\(a_n\)的正负确定数列前\(n\)项之和\(S_n\)的最值:当\(a_1<0,d>0\)时,所有负项之和最小;当\(a_1>0,d<0\)时,所有正项之和最大;
2、正项等比数列中由\(a_n\)的值的范围,确定数列前\(n\)项之积\(T_n\)的最值:当\(a_n\ge 1\)时,\(T_n\)最大;
3、求\(S_n\)的最值时,分界为\(0\);求\(T_n\)的最值时,分界为\(1\);作差法与\(0\)做大小比较,作商法与\(1\)做大小比较。
分析:当\(n\ge 1\)时,\(S_n=2a_n-2^{n+1}\)
当\(n\ge 2\)时,\(S_{n-1}=2a_{n-1}-2^n\)
两式相减得到,当\(n\ge 2\)时,\(a_n=2a_n-2a_{n-1}-(2^{n+1}-2^n)\)
整理得到,\(a_n=2a_{n-1}+2^n(n\ge 2)\), 两边同除以\(2^n\),得到
\(\cfrac{a_n}{2^n}=\cfrac{a_{n-1}}{2^{n-1}}+1(n\ge 2)\),
令\(n=1\),\(a_1=2a_1-2^2\),得到\(a_1=4\),则\(\cfrac{a_1}{2^1}=2\);
故数列\(\{\cfrac{a_n}{2^n}\}\)是以\(\cfrac{a_1}{2^1}=2\)为首项,以\(1\)为公差的等差数列,
故\(\cfrac{a_n}{2^n}=2+(n-1)\cdot1\),
即数列的\(\{a_n\}\)的通项公式为\(a_n=(n+1)2^n\)。
分析:当\(n=1\)时,\(a_1^2+2a_1=4a_1+3\),求得\(a_1=3\)或\(a_1=-1\)(舍去),
当\(n\ge 2\)时,\(a_{n-1}^2+2a_{n-1}=4S_{n-1}+3\),两式相减,
即\(n\ge 2\)时,\(a_n^2-a_{n-1}^2+2a_n-2a_{n-1}=4a_n\),
即\(n\ge 2\)时,\(a_n^2-a_{n-1}^2-2(a_n+a_{n-1})=0\),
即\(n\ge 2\)时,即\((a_n-a_{n-1})(a_n+a_{n-1})-2(a_n+a_{n-1})=0\),
由于\(a_n+a_{n-1}>0\),故得到\(a_n-a_{n-2}=2(n\ge 2)\),
故数列\(\{a_n\}\)是首项为\(3\),公差为\(2\)的等差数列,
则所求通讯公式为\(a_n=3+(n-1)\times 2=2n+1(n\in N^*)\)。
法1:并项求和法,由于题目中有\(n\)次方,故针对\(n\)分奇偶讨论如下:
①当\(n\)为奇数时,则\(n+1\)为偶数,
由题目可知\(a_{n+1}-a_n=2n-1\),\(a_{n+2}+a_{n+1}=2n+1\),
两式相减,得到\(a_{n+2}+a_n=2\),即奇数项为等和数列;
故前\(60\)项中的所有奇数项之和为
\(S_{奇}=(a_1+a_3)+(a_5+a_7)+\cdots+(a_{57}+a_{59})=15\times 2=30\);
②当\(n\)为偶数时,则\(n+1\)为奇数,
由题目可知\(a_{n+1}+a_n=2n-1\),则\(a_{n+2}-a_{n+1}=2n+1\),
两式相加,得到\(a_{n+2}+a_n=4n\),即每相邻两偶数项之和为等差数列;
故前\(60\)项中的所有偶数项之和为
\(S_{偶}=(a_2+a_4)+(a_6+a_8)+\cdots+(a_{58}+a_{60})\)
\(=4\times 2+4\times 6+4\times 10+\cdots+4\times 58\)
\(=4(2+6+10+\cdots+58)\)
\(=4\times\cfrac{(2+58)\times 15}{2}=1800\);
故\(S_{60}=1800+30=1830\)。
分析:注意到数列的项的特征,重新构造一个数列\(\{b_n\}\),
其中\(b_1=a_1=\cfrac{1}{2}\),
\(b_2=a_2+a_3=\cfrac{1}{3}+\cfrac{2}{3}=1\),
\(b_3=a_4+a_5+a_6=\cfrac{1}{4}+\cfrac{2}{4}+\cfrac{3}{4}=\cfrac{3}{2}\),
\(\cdots\)
\(b_{n-1}=\cfrac{1}{n}+\cfrac{2}{n}+\cdots+\cfrac{n-1}{n}=\cfrac{n-1}{2}\),
很显然,数列\(\{b_n\}\)是首项为\(\cfrac{1}{2}\),公差为\(\cfrac{1}{2}\)的等差数列,注意原来的数列\(\{a_n\}\)非等差非等比数列。
那么\(b_n=\cfrac{n}{2}\),其前\(n\)项和为\(T_n\),则\(T_n=\cfrac{1}{2}(\cfrac{1}{2}+\cfrac{n}{2})n=\cfrac{n(n+1)}{4}\)
令\(T_n=\cfrac{n(n+1)}{4}=S_k=14\),则\(n=7\),即对数列\(\{b_n\}\)而言,\(T_7=14\),
对数列\(\{a_n\}\)而言,它的\(S_k=T_7\),但是注意\(k\neq 0\),按照这种对应性可知\(a_k=\cfrac{7}{8}\),
如果想计算\(k\)的值,那么\(k=1+2+3+4+5+6+7=28\)。

 数列习题
数列习题

 浙公网安备 33010602011771号
浙公网安备 33010602011771号