坐标法

前言

坐标系是解析几何的基础，是联系几何与代数的桥梁，坐标系的思想是现代数学最重要的基本思想之一。在不同的坐标系中，同一几何图形可以有不同的表示形式，这使解决问题的方法有了更多的选择。

坐标法：自从坐标系产生以来，解决几何问题便多了一种方便、快捷的方法——坐标法。很多试题，当你无法找到突破口时，使用坐标法会给你一种新的启迪和数学美感。也叫解析法，主要用于解决几何中的曲线方程，有了坐标法以后，我们就可以使用代数的方法来研究曲线的性质，这也是解析几何的基本思想。

• 运用坐标法解决实际问题的步骤：建系 \(\Rightarrow\) 设点 \(\Rightarrow\) 列关系式(或方程) \(\Rightarrow\) 求解数学结果 \(\Rightarrow\) 回答实际问题.

典例剖析

在边长为 \(2\) 的正 \(\triangle ABC\) 中，若 \(P\) 为 \(\triangle ABC\) 内一点，且 \(|PA|^{2}=|PB|^{2}+|PC|^{2}\)，求点 \(P\) 的轨迹方程，并画出方程所表示的曲线。

分析：本题目是曲线方程的确定与应用问题，考查建立平面直角坐标系、数形结合思想、曲线方程的求法及分析推理、计算化间技能、技巧等。解答需要先建立平面直角坐标系，写出各点的坐标，用直接法求解，再根据方程判定曲线类型画出其表示的曲线。

解析：以 \(BC\) 所在直线为 \(x\) 轴，\(BC\) 的中点为原点，\(BC\) 的中垂线为 \(y\) 轴建立平面直角坐标系，

设 \(P(x, y)\) 是轨迹上任意一点, 又 \(|BC|=2\)， 故有 \(B(-1,0)\)， \(C(1,0)\)， 则\(A(0,\sqrt{3})\)，

由于 \(|PA|^{2}=|PB|^{2}+|PC|^{2}\)，

即 \(x^{2}+(y-\sqrt{3})^{2}=(x+1)^{2}+y^{2}+(x-1)^{2}+y^{2}\)，

化简得到， \(x^{2}+(y+\sqrt{3})^{2}=4\)，

又由于点 \(P\) 在 \(\triangle ABC\) 内， 所以 \(y>0\)，

所以， \(P\) 点的轨迹方程为 \(x^{2}+(y+\sqrt{3})^{2}=4(y>0)\).

其轨迹如图所示，为以 \((0,-\sqrt{3})\) 为圆心，半径为 \(2\) 的圆在 \(x\) 轴上方的圆弧.

〔解后反思〕用坐标法求轨迹方程的一般步骤[特别注意：在直角坐标系下和极坐标系下都是一样的]

①建立坐标系，用\((x，y)\)表示曲线上的任意一点\(M\)的坐标；

②写出适合条件\(p\)的点\(M\)的集合\(P=\{M|p(M)\}\)；

③用坐标表示条件\(p(M)\)，列出方程\(f(x，y)=0\)；

④化简方程\(f(x，y)=0\)，注意变形的等价性；

⑤检验或证明④中以方程的解为坐标的点都在曲线上，若方程的变形过程是等价的，则⑤可以省略；

【2017河北武邑中学一模，文11】在\(Rt\Delta ABC\)中，\(CA\)\(=\)\(CB\)\(=\)\(3\)，\(M\)，\(N\)是斜边\(AB\)上的两个动点，\(MN\)\(=\)\(\sqrt{2}\)，则\(\overrightarrow{CM}\)\(\cdot\)\(\overrightarrow{CN}\)的取值范围是【\(\qquad\)】

$A.[2，\cfrac{5}{2}]$ $B.[2，4]$ $C.[3，6]$ $D.[4，6]$

分析：求向量的内积的取值范围，应该想到用内积的坐标运算，本题目难点是一般想不到主动建系，由形的运算转化为数的运算。

解：如图所示，以点\(C\)为坐标原点，分别以\(CB、CA\)所在的直线为\(x、y\)轴建立如同所示的坐标系，

则\(C(0，0)\)，\(A(0，3)\)，\(B(3 ，0)\)，设点\(N\)的横坐标为\(x\)，

则由等腰直角三角形可知，点\(N\)的纵坐标为\(3-x\)，即点\(N(x，3-x)\)，

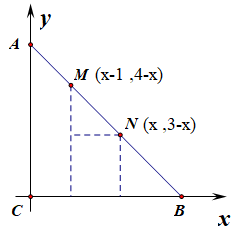
又由\(MN=\sqrt{2}\)，计算可知点\(M(x-1，4-x)\)，则\(\overrightarrow{CM}=(x-1，4-x)\)，\(\overrightarrow{CN}=(x，3-x)\)，

由于点\(M,N\)是动点，取两个极限位置研究\(x\)的取值范围，

当点\(M\)位于点\(A\)时，\(x\)取到最小值\(1\)，当点\(N\)位于点\(B\)时，\(x\)取到最大值\(3\)，即\(1\leq x\leq 3\)，

则\(\overrightarrow{CM}\cdot \overrightarrow{CN}=f(x)=((x-1，4-x)\cdot (x，3-x)\)

\(=x(x-1)+(4-x)(3-x)=2(x-2)^2+4\)，\(x\in [1，3]\)

当\(x=2\)时，\(f(x)_{min}=f(2)=4\)，当\(x=1\)或\(x=3\)时，\(f(x)_{max}=f(1)=f(3)=6\)，

即\(f(x)\in [4，6]\) . 故选\(D\) .

在 \(\triangle ABC\) 中 \(AB=3\)，\(AC=2\)，\(\angle BAC\)\(=\)\(120^{\circ}\)，点 \(D\) 为 \(BC\) 边上的一点 且 \(\overrightarrow{BD}\)\(=\)\(2\overrightarrow{DC}\)， 则 \(\overrightarrow{AB}\)\(\cdot\)\(\overrightarrow{AD}\) 等于【\(\qquad\)】

$A.\cfrac{2}{3}$ $B.1$ $C.2$ $D.\cfrac{1}{3}$

解析： 以 \(A\) 为坐标原点 \(AB\) 所在的直线为 \(x\) 轴建立平面直角坐标系如图所示.

则 \(A(0,0)\)， \(B(3,0)\)， \(C(-1, \sqrt{3})\)，

由于 \(\overrightarrow{BD}=2\overrightarrow{DC}\)， 所以 \(\overrightarrow{BD}=\cfrac{2}{3}\overrightarrow{BC}=\cfrac{2}{3}(-4,\sqrt{3})=(-\cfrac{8}{3},\cfrac{2\sqrt{3}}{3})\)，

则 \(D(\cfrac{1}{3},\cfrac{2\sqrt{3}}{3})\)， 则 \(\overrightarrow{AD}=(\cfrac{1}{3},\cfrac{2\sqrt{3}}{3})\)，\(\overrightarrow{AB}=(3,0)\)

所以， \(\overrightarrow{AB}\cdot\overrightarrow{AD}=3\times\cfrac{1}{3}+0\times\cfrac{2\sqrt{3}}{3}=1\)， 故选 \(B\) .