数学抽象

前言

新的课程标准中，给出了数学学科核心素养的六个主要方面，即数学抽象、逻辑推理、数学建模、运算能力、直观想象和数据分析，并从概念的界定、及其在数学与生活中的作用和意义方面进行了描述。

如在数学核心素养之一的数学抽象中，便指出数学抽象是指舍去事物的一切物理属性，得到数学研究对象的思维过程。给出数学抽象的作用是使得数学成为高度概括、表达准确、结论一般、有序多级的系统。数学抽象的意义，在于它是形成理性思维的重要基础。

题目原貌

【选自2021届黄冈八模测试卷一第16题】纸张的规格是指纸张制成后，经过修整切边，裁成一定的尺寸。现在我国采用国际标准，规定以 \(A_0\)、\(A_1\)、\(A_2\)、\(B_1\)、\(B_2\)、\(\cdots\) 等标记来表示纸张的幅面规格。 复印纸幅面规格只采用 \(A\) 系列和 \(B\) 系列，其中系列的幅面规格为:

(1). \(A_0\),\(A_1\),\(A_2\),\(\cdots\),\(A_8\)， 所有规格的纸张的幅宽(以 \(x\) 表示)和长度(以 \(y\) 表示 ) 的比例关系都为\(x:y=1:\sqrt{2}\)；

(2).将 \(A_0\) 纸张沿长度方向对开成两等分，便成为 \(A_1\) 规格，\(A_1\) 纸张沿长度方向对开成两等分，便成为 \(A_2\) 规格， \(\cdots\)， 如此对开至 \(A_8\) 规格。

现有 \(A_0\)、\(A_1\)、\(A_2\)、\(\cdots\)，\(A_8\) 纸各一张， 若 \(A_4\) 纸的宽度为\(2 dm\)， 则 \(A_0\) 纸的面积为 ____________ \(dm^{2}\)； 这 \(9\) 张纸的面积之和等于 ____________ \(dm^{2}\)；

• 初步解析

结合题目，我们做个示意图，大致得到如下信息，

① 每个规格的纸张的长度是宽度的 \(\sqrt{2}\) 倍，

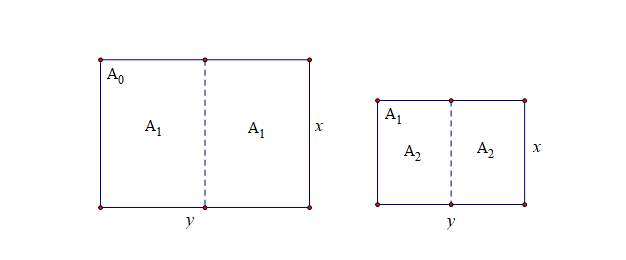
② \(A_0\) 能被等分为两个 \(A_1\)，同理，\(A_1\) 能被等分为两个 \(A_2\)，等等，

③ \(A_0\) 的宽度是 \(A_1\) 的长度，\(A_1\) 的宽度是 \(A_2\) 的长度，等等，

④ \(A\) 系列的纸张的长度能构成等比数列，\(A\) 系列的纸张的宽度能构成等比数列，

• 抽象概括

为便于表述，我们需要定义各个幅面规格，原本是 \(A_0\)、\(A_1\)、\(A_2\)、\(\cdots\)，\(A_8\) 共 \(9\) 个，

需要将其高度抽象概括，糅合为一句话，可以引入动态下标，比如不妨定义为 \(A_{i}\) (\(i=0，1，2，\cdots，8\))，

同时需要定义各个规格 \(A_{i}\) 的长度和宽度，由于每一种规格都有长度和宽度，故要注意对应性，

\(A_{i}\) (\(i=0，1，2，\cdots，8\))的纸张的长度为\(a_{i+1}\)[注意，一则数列中没有\(a_0\)，故使用\(a_{i+1}\)；二则此处还暗含了函数关系，比如当你认可了\(A_{i}\) 纸张的长度为\(a_{i+1}\)后，则\(A_{i+1}\) 纸张的长度为\(a_{i+2}\)，\(A_{i+2}\) 纸张的长度为\(a_{i+3}\)，等等如此，]，面积为\(S_{i+1}\)[注意事项同于前边]，

接下来，要寻找其中的等量关系，以便于找到解题的突破口和题目的模型，

注意到，\(A_{i+1}\) 的长度和 \(A_{i}\) 的宽度相等，故相等关系有了，只要分别表达即可。

到此，我们基本能确定，应该依托等比数列的模型来求解即可；

• 整合解析

解析：可设幅面规格为 \(A_{i}\) (\(i=0，1，2，\cdots，8\))的纸张的长度为\(a_{i+1}\)，面积为\(S_{i+1}\)，

\(A_{i}\) 的宽度为 \(\cfrac{\sqrt{2}}{2}a_{i+1}\)， \(A_{i+1}\) 的长度和 \(A_{i}\) 的宽度相等，

\(A_{i+1}\) 的长度为 \(a_{i+2}=\cfrac{\sqrt{2}}{2} a_{i+1}\)， 即\(\cfrac{a_{i+2}}{a_{i+1}}=\cfrac{\sqrt{2}}{2}\)，

故数列 \(\{a_n\}\)是以 \(\cfrac{\sqrt{2}}{2}\) 为公比的等比数列，

由题意可知，\(A_{4}\)纸的宽度为\(\cfrac{\sqrt{2}}{2}a_{5}=2\)， 故 \(a_{5}=2\sqrt{2}\)，

则\(a_{1}=\cfrac{a_{5}}{(\cfrac{\sqrt{2}}{2})^{4}}=\cfrac{2 \sqrt{2}}{\cfrac{1}{4}}=8\sqrt{2}\)，

\(A_0\) 纸的面积为 \(S_{1}=\) 长 \(\times\) 宽 \(=\cfrac{\sqrt{2}}{2}a_{1}^{2}=\cfrac{\sqrt{2}}{2}\times(8\sqrt{2})^{2}=64\sqrt{2}\) (\(dm^{2}\))

又 \(S_{1}=\cfrac{\sqrt{2}}{2}a_{1}^{2}\)，\(S_{2}=\cfrac{\sqrt{2}}{2}a_{2}^{2}\)，\(\cdots\)，则\(S_{n}=\cfrac{\sqrt{2}}{2}a_{n}^{2}\)，

则\(\cfrac{S_{n+1}}{S_{n}}=\cfrac{\cfrac{\sqrt{2}}{2}a_{n+1}^{2}}{\cfrac{\sqrt{2}}{2}a_{n}^{2}}=(\cfrac{a_{n+1}}{a_n})^2=(\cfrac{\sqrt{2}}{2})^2=\cfrac{1}{2}\)，

故数列 \(\{S_n\}\) 是以 \(64\sqrt{2}\) 为首项，以\(\cfrac{1}{2}\)为公比的等比数列，

因此，这 \(9\) 张纸的面积之和为\(\sum\limits_{i=1}^9S_{i}\)\(=\cfrac{64\sqrt{2}\times(1-\cfrac{1}{2^{9}})}{1-\cfrac{1}{2}}=\cfrac{511\sqrt{2}}{4}\) (\(dm^{2}\))

【2020-新高考全国卷I】【总结归纳抽象概括】已知公比大于 \(1\) 的等比数列 \(\{a_{n}\}\) 满足 \(a_{2}+a_{4}=20\)， \(a_{3}=8\) .

(1). 求 \(\{a_{n}\}\) 的通项公式;

解:设 \(\{a_{n}\}\) 的公比为 \(q(q>1)\)，由题设得 \(a_{1} q+a_{1}q^{3}=20\)，\(a_{1}q^{2}=8\).

整理得， \(2q^{2}-5q+2=0\)， 即 \((2q-1)(q-2)=0\)，

解得 \(q=\cfrac{1}{2}\) (舍去)， \(q=2\)，故由题设得 \(a_{1}=2\)，

所以 \(\{a_{n}\}\) 的通项公式为 \(a_{n}=2^{n}\) .

(2).[难点部分] 记 \(b_{m}\) 为 \(\{a_{n}\}\) 在区间 \((0, m]\)\((m\in {N}^{*})\) 中的项的个数， 求数列 \(\{b_{m}\}\) 的前 \(100\) 项和 \(S_{100}\).

分析：由题目首先写成数列 \(\{a_n\}\)的前有限项备用，\(a_1=2\)，\(a_2=4\)，\(a_3=8\)，\(a_4=16\)，\(a_5=32\)，\(\cdots\)，

当 \(m=1\)时，区间为 \((0,1]\)，故 \(b_1=0\)；

解析：

当\(m=1\)时，区间为\((0,1]\)，则\(b_1=0\)；

当\(m=2\)时，区间为\((0,2]\)，则\(b_2=1\)；

当\(m=3\)时，区间为\((0,3]\)，则\(b_3=1\)；其和为 \(1\times 2^1\)；

当\(m=4\)时，区间为\((0,4]\)，则\(b_4=2\)；

当\(m=5\)时，区间为\((0,5]\)，则\(b_5=2\)；

当\(m=6\)时，区间为\((0,6]\)，则\(b_6=2\)；

当\(m=7\)时，区间为\((0,7]\)，则\(b_7=2\)；其和为 \(2\times 2^2\)；同时注意，当我们写道这里时，往往心里已经有底了，

当\(m=8\)时，区间为\((0,8]\)，则\(b_8=3\)；

当\(m=9\)时，区间为\((0,9]\)，则\(b_9=3\)；

\(\cdots\)；

当\(m=15\)时，区间为\((0,15]\)，则\(b_{15}=3\)；其和为 \(3\times 2^3\)；从 \(8\) 到 \(15\) 的个数计算用等差数列来求解，是\(\cfrac{15-8}{1}\) \(+\) \(1\)\(=\)\(8\)个，其他的依此类推即可；

当\(m=16\)时，区间为\((0,16]\)，则\(b_{16}=4\)；

当\(m=17\)时，区间为\((0,17]\)，则\(b_{17}=4\)；

\(\cdots\)；

当\(m=31\)时，区间为\((0,31]\)，则\(b_{31}=4\)；其和为 \(4\times 2^4\)；

当\(m=32\)时，区间为\((0,32]\)，则\(b_{32}=5\)；

当\(m=33\)时，区间为\((0,33]\)，则\(b_{33}=5\)；

\(\cdots\)；

当\(m=63\)时，区间为\((0,63]\)，则\(b_{63}=5\)；其和为 \(5\times 2^5\)；

当\(m=64\)时，区间为\((0,64]\)，则\(b_{64}=6\)；

当\(m=65\)时，区间为\((0,65]\)，则\(b_{65}=6\)；

\(\cdots\)；

当\(m=100\)时，区间为\((0,100]\)，则\(b_{100}=6\)；其和为 \(6\times(100-63)\)；从 \(64\) 到 \(100\) 的个数计算用等差数列来求解，是\(\cfrac{100-64}{1}\) \(+\) \(1\)\(=\)\(37\)个，或者用\(100\)\(-\)\(63\)\(=\)\(37\)；

所以 \(S_{100}=b_{1}+\left(b_{2}+b_{3}\right)+\left(b_{4}+b_{5}+b_{6}+b_{7}\right)+\cdots+\left(b_{32}+b_{33}+\cdots+b_{63}\right)+\left(b_{64}+b_{65}\right.\)

\(\left.+\cdots+b_{100}\right)=0+1 \times 2+2 \times 2^{2}+3 \times 2^{3}+4 \times 2^{4}+5 \times 2^{5}+6 \times(100-63)=480\).

[高阶解法]：(如果能理解上述的分析求解过程，则我们可以采用更加抽象的表达形式来刻画)

由题设及(1)知 \(b_{1}=0\), 且当 \(2^{n}\leqslant m<2^{n+1}\) 时, \(b_{m}=n\).

所以 \(S_{100}=b_{1}+(b_{2}+b_{3})+(b_{4}+b_{5}+b_{6}+b_{7})+\cdots+(b_{32}+b_{33}+\cdots+b_{63})+(b_{64}+b_{65}\)

\(+\cdots+b_{100})=0+1\times2+2\times 2^{2}+3\times 2^{3}+4\times 2^{4}+5\times 2^{5}+6\times(100-63)=480\).