三角函数公式关系梳理

前言

同角公式

平方关系：^[1]

$sin^2\theta+cos^2\theta=1$

商数关系：

\[\cfrac{sin\theta}{cos\theta}=tan\theta \]

• 同角三角函数基本关系公式，强调的是同角，只要角的形式相同即可，比如\(\sin^2(2x+\cfrac{\pi}{3})+\cos^2(2x+\cfrac{\pi}{3})=1\)一定成立，但是 \(\sin^2(2x+\cfrac{\pi}{3})+\cos^2(2x+\cfrac{\pi}{6})=1\)就不一定成立。

诱导公式

公式	一[角的终 边相同]	二[关于原 点对称]	三[关于\(x\) 轴对称]	四[关于\(y\) 轴对称]	五[关于直线 \(y=x\)对称]	六[旋转\(\cfrac{\pi}{2}\) 的对称性[2]]
角的大小	\(2k\pi+\alpha\)	\(\pi+\alpha\)	\(-\alpha\)	\(\pi-\alpha\)	\(\cfrac{\pi}{2}-\alpha\)	\(\cfrac{\pi}{2}+\alpha\)
正弦\(\Rightarrow\sin\)	\(sin\alpha\)	\(-sin\alpha\)	\(-sin\alpha\)	\(sin\alpha\)	\(cos\alpha\)	\(cos\alpha\)
余弦\(\Rightarrow\cos\)	\(cos\alpha\)	\(-cos\alpha\)	\(cos\alpha\)	\(-cos\alpha\)	\(sin\alpha\)	\(-sin\alpha\)
正切\(\Rightarrow\tan\)	\(tan\alpha\)	\(tan\alpha\)	\(-tan\alpha\)	\(-tan\alpha\)	\(\cot\alpha\)最后两个诱导公式不要求掌握；	\(-\cot\alpha\)
记忆口诀	函数名不变 符号看象限	函数名不变 符号看象限	函数名不变 符号看象限	函数名不变 符号看象限	函数名改变 符号看象限	函数名改变 符号看象限

[解释]诱导公式可简记为：奇变偶不变，符号看象限．

(1)“奇”“偶”指的是“\(k\cdot\cfrac{\pi}{2}＋α(k∈Z)\)”中的\(k\)是奇数还是偶数；“变”与“不变”是指函数的名称的变化，若\(k\)是奇数，则正、余弦互变，若\(k\)为偶数，则函数名称不变．

(2)“符号看象限”指的是在“\(k\cdot\cfrac{\pi}{2}＋α(k∈Z)\)”中，将\(α\)看成锐角时，“\(k\cdot\cfrac{\pi}{2}＋α(k∈Z)\)”的终边所在的象限．

和差角公式

\[sin(\alpha\pm \beta)=sin\alpha\cdot cos\beta \pm cos\alpha\cdot sin\beta \]

\[cos(\alpha\pm \beta)=cos\alpha\cdot cos\beta \mp sin\alpha\cdot sin\beta \]

\[tan(\alpha\pm \beta)=\cfrac{tan\alpha\pm tan\beta}{1\mp tan\alpha\cdot tan\beta} \]

关系梳理

• 和差角公式是诱导公式的拓展，诱导公式是和差角公式的特例；二者是特殊与一般的关系。以 \(C_{(\alpha-\beta)}\)为例，

$C_{(\alpha-\beta)}\Rightarrow\left\{\begin{array}{l} \xrightarrow{-\beta=2k\pi ，k\in Z} &\cos(2k\pi+\alpha)=\cos\alpha\\ \xrightarrow{-\beta=\pi} &\cos(\pi+\alpha)=-\cos\alpha\\ \xrightarrow{\alpha=0} &\cos(-\beta)=\cos\beta\\ \xrightarrow{\alpha=\pi} &\cos(\pi-\beta)=-\cos\beta\\ \xrightarrow{\alpha=\cfrac{\pi}{2}} &\cos(\cfrac{\pi}{2}-\beta)=\sin\beta\\ \xrightarrow{-\beta=\cfrac{\pi}{2}} &\cos(\cfrac{\pi}{2}+\alpha)=-\sin\alpha \end{array}\right.\quad$

举例说明：当\(sin(\alpha+\beta)\)中涉及到的角比较特殊时，比如\(\alpha=\cfrac{3\pi}{2}\)时，我们走诱导公式这条线比较快捷，即\(sin(\alpha+\beta)=sin(\cfrac{3\pi}{2}+\beta)=-cos\beta\)；

当涉及到的角非常一般时，我们只能走和差角公式这条线，即\(sin(\alpha+\beta)=sin\alpha\cdot cos\beta+cos\alpha\cdot sin\beta\)；

• 三角形中的三角函数关系，其实质是诱导公式在三角形中的应用；

\(sin(A+B)=sin(\pi-C)=sinC\)，\(cos(A+B)=cos(\pi-C)=-cosC\)，

\(sin\cfrac{A+B}{2}=sin(\cfrac{\pi}{2}-\cfrac{C}{2})=cos\cfrac{C}{2}\)，\(cos\cfrac{A+B}{2}=cos(\cfrac{\pi}{2}-\cfrac{C}{2})=sin\cfrac{C}{2}\)，

应用注意

• 互通

由诱导公式我们知道，\(sin(\cfrac{\pi}{2}-\alpha)=cos\alpha\)；

由和差角公式我们知道，以下的使用也是正确的，

\(sin(\cfrac{\pi}{2}-\alpha)=sin\cfrac{\pi}{2}cos\alpha-cos\cfrac{\pi}{2}sin\alpha=cos\alpha\)；

但是二者学习成本相比，记住诱导公式的结论，非常有必要；

• 不互通，下列公式中的\(\alpha\)，\(\beta\)，\(\alpha-\beta\)都受限，需要\(\neq k\pi+\cfrac{\pi}{2}\)；

\(tan(\alpha-\beta)=\cfrac{tan\alpha-tan\beta}{1+tan\alpha\cdot tan\beta}\)，

所以以下的变形是错误的，应该避免：

\(tan(\cfrac{\pi}{2}-\alpha)=\cfrac{tan\cfrac{\pi}{2}-tan\alpha}{1+tan\cfrac{\pi}{2}\cdot tan\alpha}\)

正确的变形应该是用诱导公式：\(\tan(\cfrac{\pi}{2}-\alpha)=\cfrac{1}{\tan\alpha}=\cot\alpha\)；

典例剖析

【2020届宝鸡市质量检测1理科数学第15题】在\(\triangle ABC\)中，\(\angle ABC=90^{\circ}\)，\(AB=4\)，\(BC=3\)，点\(D\)在线段\(AC\)上，若\(\angle BDC=60^{\circ}\)，则\(BD\)=___________，\(cos\angle CBD\)=_____________。

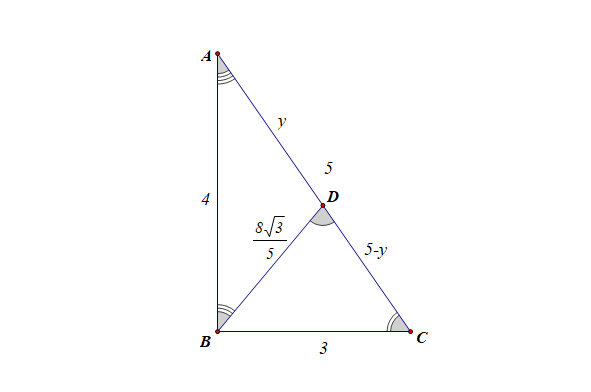
分析：由题可知，\(sinC=\cfrac{4}{5}\)，\(cosC=\cfrac{3}{5}\)，

在\(\triangle BCD\)中，由正弦定理可知，\(\cfrac{BD}{sinC}=\cfrac{3}{sin60^{\circ}}\)，解得\(BD=\cfrac{8\sqrt{3}}{5}\)；

\(cos\angle CBD=cos[\pi-(\angle BDC+\angle ACB)]=-cos(\angle BDC+\angle ACB)\)

\(=-cos60^{\circ}\cdot cos\angle ACB+\)\(sin60^{\circ}\cdot sin\angle ACB\)

\(=-\cfrac{3}{10}+\cfrac{4\sqrt{3}}{10}=\cfrac{4\sqrt{3}-3}{10}\).

解后反思：如果利用余弦定理求解\(AD\)，再用正弦定理求解\(sin\angle ABD\)，利用\(cos \angle CBD=sin\angle ABD\)，从而求得\(cos \angle CBD\)，这样的运算会很复杂。这个题目的求解也从另一个角度说明了公式\(cos(\alpha+\beta)\)存在的必要性。

---

1. 注意公式的变形形式，加减开方等变形，如 \(\sin^2\theta=1-\cos^2\theta\)， \(\sin\theta=\pm\sqrt{1-\cos^2\theta}\)，乘除等变形，如 \(\cfrac{\cos^2\theta}{1-\sin^2\theta}\)\(=\)\(1\)，\(\cfrac{\cos\theta}{\sin\theta-1}\)\(\cdot\)\(\cfrac{\cos\theta}{\sin\theta+1}\)\(=\)\(-1\)，同样的思路，也可以表达商数关系，如分式变整式，\(\sin\theta=\cos\theta\cdot\tan\theta\)。 ↩︎

2. 或是两次轴对称刻画，首先关于\(y=x\)对称，得到角\(\cfrac{\pi}{2}-\alpha\)，再将得到的角关于\(y\)轴对称，就得到了角\(\cfrac{\pi}{2}+\alpha\)；或用一次旋转刻画，将角\(\alpha\)逆时针旋转\(\cfrac{\pi}{2}\)，就得到角\(\cfrac{\pi}{2}+\alpha\) . ↩︎