整合与拆分
整合与拆分是高中数学中一种比较常见的变形技巧，既是一种数学能力和数学素养，也是数学创新和数学应用意识的一种外在体现。其本质应该归属于数学转化划归思想中。
前言
整合与拆分是高中数学中一种比较常见的变形技巧，既是一种数学能力和数学素养，也是数学创新和数学应用意识的一种外在体现。其本质应该归属于数学转化划归思想中。下文以案例具体加以说明。
本博文适合数学功底比较好的学生阅读。相关阅读能合二为一或一分为二的数学素材；
均值不等式
解析： 因为 \(a=\cfrac{1}{2}[(a+b)+(a-b)]\)，变形说明要特别注意此处的对变量 \(a\)的拆分技巧，非常类似于三角函数中的对角的拆分技巧，比如\(\alpha\)\(=\)\(\cfrac{1}{2}\)\([\)\((\)\(\alpha\)\(+\)\(\beta\)\()\)\(+\)\((\)\(\alpha\)\(-\)\(\beta\)\()\)\(]\)，此处做这样的变形，其目的是为了消去后面的两个分母；；
所以 \(a+\cfrac{4}{a+b}+\cfrac{1}{a-b}\)
\(=\cfrac{1}{2}(a+b)+\cfrac{4}{a+b}+\cfrac{1}{2}(a-b)+\cfrac{1}{a-b}\)
因为 \(a>b>0\)， 所以 \(a+b>0\)， \(a-b>0\)，
由基本不等式可得 \(\cfrac{1}{2}(a+b)+\cfrac{4}{a+b}\geqslant 2\sqrt{\cfrac{1}{2}(a+b)\times\cfrac{4}{a+b}}=2\sqrt{2}\)①，
当且仅当 \(\cfrac{1}{2}(a+b)=\cfrac{4}{a+b}\)， 即 \(a+b=2\sqrt{2}\)时， 等号成立；
\(\cfrac{1}{2}(a-b)+\cfrac{1}{a-b}\geqslant 2\sqrt{\cfrac{1}{2}(a-b)\times\cfrac{1}{a-b}}=\sqrt{2}\)②，
当且仅当 \(\cfrac{1}{2}(a-b)=\cfrac{1}{a-b}\)， 即 \(a-b=\sqrt{2}\) 时，等号成立.
由 \(\left\{\begin{array}{l}a+b=2\sqrt{2}\\a-b=\sqrt{2}\end{array}\right.\)，解得 \(\left\{\begin{array}{l}a=\cfrac{3\sqrt{2}}{2}\\b=\cfrac{\sqrt{2}}{2}\end{array}\right.\)
所以当 \(\left\{\begin{aligned}a=\cfrac{3\sqrt{2}}{2}\\b=\cfrac{\sqrt{2}}{2} \end{aligned}\right.\)时，①②中的等号同时成立.
故 \(a+\cfrac{4}{a+b}+\cfrac{1}{a-b}\) 的最小值为 \(2\sqrt{2}+\sqrt{2}=3\sqrt{2}\)，故选 \(D\).
函数与方程
比如求函数零点时，对函数的有效拆分或者整合。
分析：求解函数的零点个数的思路和方法有三个：
①解方程法；②数形结合法；③零点存在性定理法；本题目适合使用方法②；
由函数零点的定义，得到表达式\(2^x|log_{0.5}x|-1=0\)，接下来的两种不同的拆分方式：
①\(2^x|log_{0.5}x|=1\)，不好，左边的函数图像不容易作；
②\(|log_{0.5}x|=\cfrac{1}{2^x}=(\cfrac{1}{2})^x\)，好，左右两端的函数的图像都能顺利做出；
由图像可知，两个函数的图像的交点有\(2\)个，故原函数的零点个数是\(2\)个。
分析：本题目肯定会用到数形结合的方法思路。难点是函数的拆分。
法1：拆分为\(h(x)=\left\{\begin{array}{l}{x,x\leqslant 0}\\{e^x+x,x>0}\end{array}\right.=m\)，做出示意图如下，
由图可知，\(m\in (-\infty,0]\cup(1,+\infty)\)
法2：拆分为\(f(x)=-x+m\)，做出示意图如下，
由图可知，\(m\in (-\infty,0]\cup(1,+\infty)\)
解后反思：法1的难点是函数\(h(x)\)图像的做法；法2的难点是利用直线\(y=-x+m\)的\(m\)的几何意义确定其值的范围；
分析：这类题目一般需要用到拆分，但本题目需要用到整合，通过做差构造函数，
令\(f(x)=x^3-(\cfrac{1}{2})^{x-2}\)，函数的定义域为\(R\)，且为增函数，
又由于\(f(1)=-1<0\)，\(f(2)=7>0\)，故\(x_0\)所在的区间为\((1,2)\).
复合函数
引例1：研究函数\(y=(\cfrac{1}{2})^{2x^2+3x-1}\)的单调性时，拆分为\(y=(\cfrac{1}{2})^u\)和\(u=2x^2+3x-1\)两个函数，则其单调性就好研究；
引例2：研究函数\(y=5^{1-|x-2|}\)的单调性时，拆分为\(y=5^u\)和\(u=1-|x-2|\)两个函数，则其单调性就好研究；
三角函数
角的拆分和整合
\((\cfrac{\pi}{4}+\theta)+(\cfrac{\pi}{4}-\theta)=\cfrac{\pi}{2}\)；\((\cfrac{\pi}{3}+\theta)+(\cfrac{\pi}{6}-\theta)=\cfrac{\pi}{2}\)；
\(2x\pm\cfrac{\pi}{2}=2(x\pm\cfrac{\pi}{4})\)；\(2\alpha\pm\cfrac{\pi}{3}=2(\alpha\pm\cfrac{\pi}{6})\)；
- 常见的配角技巧：
\(2\alpha=(\alpha+\beta)+(\alpha-\beta)\)；\(2\beta=(\alpha+\beta)-(\alpha-\beta)\)；
\(3\alpha-\beta=2(\alpha-\beta)+(\alpha-\beta)\)；\(3\alpha+\beta=2(\alpha+\beta)+(\alpha-\beta)\)；
\(\alpha=(\alpha+\beta)-\beta\)；\(\beta=\alpha-(\alpha-\beta)\)；
\(\alpha=\cfrac{\alpha+\beta}{2}+\cfrac{\alpha-\beta}{2}\)；\(\beta=\cfrac{\alpha+\beta}{2}-\cfrac{\alpha-\beta}{2}\)；
\(\alpha=(\alpha+\beta)-\beta\)；\((\cfrac{\pi}{6}-\alpha)+(\cfrac{\pi}{3}+\alpha)=\cfrac{\pi}{2}\)；\((\cfrac{\pi}{4}-\alpha)+(\cfrac{\pi}{4}+\alpha)=\cfrac{\pi}{2}\)；
\((\cfrac{\pi}{3}-\alpha)+(\cfrac{2\pi}{3}+\alpha)=\pi\)；\((\cfrac{\pi}{4}-\alpha)+(\cfrac{3\pi}{4}+\alpha)=\pi\)；
\(sin(\alpha-\beta)\cdot cos\beta+cos(\alpha-\beta)\cdot sin\beta=\cfrac{1}{3}\)，即整合为\(sin[(\alpha-\beta)+\beta]=sin\alpha=\cfrac{1}{3}\)；
\(1+sin\theta+cos\theta=1+cos\theta+sin\theta=2cos^2\cfrac{\theta}{2}+2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}=2cos\cfrac{\theta}{2}(cos\cfrac{\theta}{2}+sin\cfrac{\theta}{2})\)
\(1+sin\theta-cos\theta=1-cos\theta+sin\theta=2sin^2\cfrac{\theta}{2}+2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}=2sin\cfrac{\theta}{2}(cos\cfrac{\theta}{2}+sin\cfrac{\theta}{2})\)
\(1-sin\theta+cos\theta=1+cos\theta-sin\theta=2cos^2\cfrac{\theta}{2}-2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}=2cos\cfrac{\theta}{2}(cos\cfrac{\theta}{2}-sin\cfrac{\theta}{2})\)
\(1-sin\theta-cos\theta=1-cos\theta-sin\theta=2sin^2\cfrac{\theta}{2}-2sin\cfrac{\theta}{2}cos\cfrac{\theta}{2}=2sin\cfrac{\theta}{2}(sin\cfrac{\theta}{2}-cos\cfrac{\theta}{2})\)
分离参数
- 分离参数时，尽可能的使函数形式简单，这样求导数判断单调性就简单些，而参数形式复杂些或者简单些都无所谓，
(1)若函数\(f(x)\)在区间\((0，\cfrac{1}{2})\)上无零点，求实数\(a\)的最小值。
【法1】(分离参数，参数形式简单，函数复杂)
碰到这类问题，我们的第一反应往往是分离参数，然后数形结合求解，但是这个方法不见得是很恰当和很灵活的。
先变形为\(a(1-x)=2+2lnx-2x\)，再分离参数为\(a=\cfrac{2+2lnx-2x}{1-x}\)，其中\(x\in (0，\cfrac{1}{2})\)，
令函数\(h(x)=\cfrac{2+2lnx-2x}{1-x}\)，接下来用导数研究单调性，准备做函数的大值图像，
\(h'(x)=\cfrac{(\cfrac{2}{x}-2)(1-x)-(2+2lnx-2x)(-1)}{(1-x)^2}=\cfrac{2lnx+\cfrac{2}{x}-2}{(1-x)^2}\)
暂时没法看透\(h'(x)\)的正负值，也无法判断原函数\(h(x)\)的增减性，
故再设\(h'(x)\)的分子函数为\(m(x)=2lnx+\cfrac{2}{x}-2\)，
\(m'(x)=\cfrac{2}{x}-\cfrac{2}{x^2}=\cfrac{2x-2}{x^2}\)，
由于\(0< x <\cfrac{1}{2}\)，故\(m'(x) <0\)，即\(m(x)\)单调递减，
故函数\(m(x)\)的最小值的极限为\(m(\cfrac{1}{2})=2ln\cfrac{1}{2}+4-2=2(1-ln2)>0\)
编外话：由分子函数\(m(x)\)的最小值的极限为正，说明函数\(h'(x)\)的分子都为正，
故\(h'(x)=\cfrac{m(x)}{(1-x)^2}>0\)，故函数\(h(x)\)在\(x\in (0，\cfrac{1}{2})\)上单调递增，
故\(h(x)\)的最大值的极限为\(h(\cfrac{1}{2})=\cfrac{2+2ln\cfrac{1}{2}-2\times\cfrac{1}{2}}{1-\cfrac{1}{2}}=2(1-2ln2)\)
要使直线\(y=a\)与函数\(y=h(x)(0< x <\cfrac{1}{2})\)没有交点，
则\(a\)的取值范围是\(a\ge 2(1-2ln2)\)，故\(a_{min}=2-4ln2\)。
【法2】(分离参数，参数形式复杂，函数简单)
将原方程\((2-a)x-2(1+lnx)+a=0\)，先变形为\((2-a)x+(a-2)-2lnx=0\)，再变形为\(\cfrac{2-a}{2}=\cfrac{lnx}{x-1}\)，
令\(h(x)=\cfrac{lnx}{x-1}\)，
则\(h'(x)=\cfrac{\cfrac{1}{x}(x-1)-lnx}{(x-1)^2}=\cfrac{1-\cfrac{1}{x}-lnx}{(x-1)^2}\)
令\(m(x)=1-\cfrac{1}{x}-lnx\)，
则\(m'(x)=\cfrac{1}{x^2}-\cfrac{1}{x}=\cfrac{1-x}{x^2}>0\)在\((0，\cfrac{1}{2})\)上恒成立，
故函数\(m(x)\)在\((0，\cfrac{1}{2})\)单调递增，
故\(m(x)_{max}\)的极限为\(m(\cfrac{1}{2})=1-2-ln\cfrac{1}{2}=ln2-1<0\)
则函数\(h'(x)=\cfrac{m(x)}{(x-1)^2}<0\)在\((0，\cfrac{1}{2})\)上恒成立，
函数\(h(x)\)在\((0，\cfrac{1}{2})\)上单调递减，
则\(h(x)_{min}\)的极限为\(h(\cfrac{1}{2})=\cfrac{ln\cfrac{1}{2}}{\cfrac{1}{2}-1}=2ln2\)
要使得原方程无解，必须满足函数\(y=\cfrac{2-a}{2}\)与函数\(y=h(x)\)没有交点，
即\(\cfrac{2-a}{2}\leq 2ln2\)，即\(a\ge 2-4ln2\)
故\(a_{min}=2-4ln2\)。
数列变形
法1：整体思想，由已知容易知道数列\(\{na_n\}\)是首项为1，公差为0的等差数列，
故\(na_n=1+(n-1)\cdot 0\)，即\(a_n=\cfrac{1}{n}(n\in N^*)\)。
法2：累乘法，拆分变形为\(\cfrac{a_{n+1}}{a_n}=\cfrac{n}{n+1}\)，由此式子可得到
以上\(n-1\)个式子相乘得到，当\(n\ge 2\)时，
\(\cfrac{a_n}{a_{n-1}}\cdot \cfrac{a_{n-1}}{a_{n-2}}\cdot \cfrac{a_{n-2}}{a_{n-3}}\cdot \cdots \cfrac{a_2}{a_1}=\cfrac{n-1}{n} \cdot \cfrac{n-2}{n-1} \cdot\cfrac{n-3}{n-2}\cdot \cdots\cfrac{1}{2}\)，
即\(\cfrac{a_n}{a_1}=\cfrac{1}{n}\)，故\(a_n=\cfrac{1}{n}(n\ge 2)\)，
当\(n=1\)时，\(a_1=1\)满足上式，故所求通项公式\(a_n=\cfrac{1}{n}(n\in N^*)\)。
- 如已知\(a_n=(2n-1)\cdot 2^n\)，求数列\(\{a_n\}\)的前\(n\)项和时，需要将其两个因子数列拆分为等差数列\(b_n=2n-1\)和等比数列\(c_n=2^n\)，以便于利用错位求和法求和。
其项数的计算，将其上标拆分出来计算，其上标刚好成等差数列，
故项数\(r=\cfrac{a_n-a_1}{d}+1=\cfrac{(2n+3)-1}{3-1}+1=n+2\)；
则\(S=\cfrac{2\cdot (4^{n+2}-1)}{4-1}=\cfrac{2}{3}(4^{n+2}-1)\)。
法1：并项求和法[此法运算和思维成本最小]，由于题目中有\(n\)次方，故针对\(n\)分奇偶讨论如下：
①当\(n\)为奇数时，则\(n+1\)为偶数，
由题目可知\(a_{n+1}-a_n=2n-1\)，则\(a_{n+2}+a_{n+1}=2n+1\)[1]
两式相减，得到\(a_{n+2}+a_n=2\)，即从\(a_1\)开始，相邻两个奇数项为等和数列；
即\(a_1+a_3=2\)，\(a_5+a_7=2\)，\(a_9+a_{11}=2\)，\(\cdots\)，\(a_{57}+a_{59}=2\)，
故前\(60\)项中的所有奇数项之和为
\(S_{奇}=(a_1+a_3)+(a_5+a_7)+\cdots+(a_{57}+a_{59})=15\times 2=30\)；
②当\(n\)为偶数时，则\(n+1\)为奇数，
由题目可知\(a_{n+1}+a_n=2n-1\)，则\(a_{n+2}-a_{n+1}=2n+1\)[原因同上]，
两式相加，得到\(a_{n+2}+a_n=4n\)，即每相邻两偶数项之和为等差数列；
故前\(60\)项中的所有偶数项之和为
\(S_{偶}=(a_2+a_4)+(a_6+a_8)+\cdots+(a_{58}+a_{60})\)
\(=4\times 2+4\times 6+4\times 10+\cdots+4\times 58\)
\(=4(2+6+10+\cdots+58)\)
\(=4\times\cfrac{(2+58)\times 15}{2}=1800\)；
故\(S_{60}=1800+30=1830\)。
思路2[摘编自网络，学习变形]：从特殊到一般，
对于给出的递推数列，在没有找到更好方法之前，通常可以用特殊值法开路，写出前几项，先归纳，再猜想一般的规律。
设\(a_1=a\)，由递推公式\(a_{n+1}+(-1)^n\cdot a_n=2n-1\)，
分别令\(n=1,2,3,4,\cdots\)，则有
\(a_2=1+a\)，\(a_3=2-a\)，\(a_4=7-a\)，\(a_5=a\)，
\(a_6=9+a\)，\(a_7=2-a\)，\(a_8=15-a\)，\(a_9=a\)，\(\cdots\)，
于是可知，\(a_{4k-3}=a\)，\(a_{4k-2}=a+(8k-7)\)，\(a_{4k-1}=2-a\)，\(a_{4k}=-a+(8k-1)\)，[2]
所以，\(a_{4k-3}+a_{4k-2}+a_{4k-1}+a_{4k}=16k-6\)，
可知每连续四项之和成等差数列，
则\(S_{60}=\cfrac{15[10+(16\times 15-6)]}{2}=1830\)；
思路3[摘编自网络，学习变形]：分类讨论，
本题目的难点在于\((-1)^n\)，于是对其分类讨论，并进行适当的构造以及并项。
当\(n\)为奇数时，\(a_{n+1}-a_n=2n-1\)；
当\(n\)为偶数时，\(a_{n+1}+a_n=2n-1\)；
于是\(a_{4k}+a_{4k-1}+a_{4k-2}+a_{4k-3}=(a_{4k}-a_{4k-1})+2(a_{4k-1}+a_{4k-2})-(a_{4k-2}-a_{4k-3})\)[3]
\(=[2(4k-1)-1]+2[2(4k-2)-1]-[2(4k-3)-1]=16k-6\)，
可知每连续四项之和成等差数列，
则\(S_{60}=\cfrac{15[10+(16\times 15-6)]}{2}=1830\)；
思路4[摘编自网络，学习变形]：利用迭代法，
对于给出的递推数列问题，应该关注三个技巧----迭加、迭乘、迭代。特别是迭代法，它是直接反复利用递推公式而进行迭代，可以直接运用，从而使得问题得以解决。
由\(a_{n+1}+(-1)^n\cdot a_n=2n-1\)得到[用\(n+1\)替换左式中的\(n\)]，\(a_{n+2}+(-1)^{n+1}\cdot a_{n+1}=2(n+1)-1\)，
则\(a_{n+2}=-(-1)^{n+1}\cdot a_{n+1}+2n+1\)，
\(=(-1)^{n}\cdot a_{n+1}+2n+1\) [将已知式改写为\(a_{n+1}=(-1)^{n+1}a_n+2n-1\)，代入左式，得到下式]
\(=(-1)^n[(-1)^{n+1}a_n+2n-1]+2n+1\)
\(=-a_n+(-1)^{n}(2n-1)+2n+1\)
即\(a_{n+2}+a_n=(-1)^{n}(2n-1)+2n+1\)
也有\(a_{n+3}+a_{n+1}=-(-1)^{n}(2n+1)+2n+3\)[让上式中\(n+1\rightarrow n\)得到]
两式相加得到\(a_n+a_{n+1}+a_{n+2}+a_{n+3}=-2(-1)^n+4n+4\)，
设\(k\)为整数[或令\(n=4k+1\)]，则
\(a_{4k+1}+a_{4k+2}+a_{4k+3}+a_{4k+4}=-2(-1)^{4k+1}+4(4k+1)+4=16k+10\)
于是\(S_{60}=\sum\limits_{k=0}^{14}{(a_{4k+1}+a_{4k+2}+a_{4k+3}+a_{4k+4})}\)[4]
\(=\sum\limits_{k=0}^{14}{(16k+10)}=(16\times 0+10)+(16\times 1+10)+(16\times 2+10)+\cdots+(16\times 14+10)\)
\(=16\times \cfrac{(0+14)\times 15}{2}+150=1830\)
思路5[摘编自网络，学习变形]：构造子数列法，
\(\{a_n\}\)既不是等差数列也不是等比数列，但是可以发现其子数列\(\{a_{4k}\}\)，\(\{a_{4k-1}\}\)，\(\{a_{4k-2}\}\)，\(\{a_{4k-3}\}\)是等差数列，于是可对数列\(\{a_n\}\)分项击破，
当\(n\)为奇数时，\(a_{n+1}-a_n=2n-1\)；
当\(n\)为偶数时，\(a_{n+1}+a_n=2n-1\)；
由\(a_{4k+2}-a_{4k-2}=(a_{4k+2}-a_{4k+1})+(a_{4k+1}+a_{4k})-(a_{4k}-a_{4k-1})-(a_{4k-1}+a_{4k-2})\)，[5]
\(=[2(4k+1)-1]+(2\times 4k-1)-[2(4k-1)-1]-[2(4k-2)-1]=8\)，
故数列\(a_{4k-2}\)是等差数列，公差为\(8\)，首项为\(a_2\)，所以\(a_{4k-2}=a_2+(k-1)8\)；
由\(a_{4k+4}-a_{4k}=(a_{4k+4}-a_{4k+3})+(a_{4k+3}+a_{4k+2})-(a_{4k+2}-a_{4k+1})-(a_{4k+1}+a_{4k})\)，[6]
\(=[2(4k+3)-1]+[2(4k+2)-1)-[2(4k+1)-1]-[2\times 4k-1]=8\)，
故数列\(a_{4k}\)是等差数列，公差为\(8\)，首项为\(a_4\)，所以\(a_{4k}=a_4+(k-1)8\)；[7]
同理，\(a_{4k+1}-a_{4k-3}=0\)，故数列\(\{a_{4k-3}\}\)是常数列，故\(a_{4k-3}=a_1\)；
\(a_{4k+3}-a_{4k-1}=0\)，故数列\(\{a_{4k-1}\}\)是常数列，故\(a_{4k-1}=a_3\)；
又\(a_1+a_2+a_3+a_4=(a_4-a_3)+2(a_3+a_2)-(a_2-a_1)\)
\(=(2\times 3-1)+2(2\times 2-1)-(2\times 1-1)=5+6-1=10\);
于是\(\{a_n\}\)的前\(60\)项的和\(S_{60}\)为
\(S_{60}=(a_1+a_5+a_9+\cdots+a_{57})+(a_2+a_6+a_{10}+\cdots+a_{58})\)[8]
\(+(a_3+a_7+a_{11}+\cdots+a_{59})+(a_4+a_8+a_{12}+\cdots+a_{60})\)
\(=15a_1+(15a_2+840)+15a_3+(15a_4+840)\)
\(=15(a_1+a_2+a_3+a_4)+1680=1830\)
思路6[摘编自网络，学习变形]：构造等差数列法，
由上述解法不难看出，本题目的实质是连续四项的和成等差数列，故还可以如下求解：
当\(n\)为奇数时，\(a_{n+1}-a_n=2n-1\)；
当\(n\)为偶数时，\(a_{n+1}+a_n=2n-1\)；
由\(a_{4k+2}-a_{4k-2}=(a_{4k+2}-a_{4k+1})+(a_{4k+1}-a_{4k})-(a_{4k}-a_{4k-1})-(a_{4k-1}+a_{4k-2})\)，
\(=[2(4k+1)-1]+(2\times 4k-1)-[2(4k-1)-1]-[2(4k-2)-1]=8\)，
故数列\(a_{4k-2}\)是等差数列，公差为\(8\)，首项为\(a_2\)，所以\(a_{4k-2}=a_2+(k-1)8\)；
由\(a_{4k+4}-a_{4k}=(a_{4k+4}-a_{4k+3})+(a_{4k+3}+a_{4k+2})-(a_{4k+2}-a_{4k+1})-(a_{4k+1}+a_{4k})\)，
\(=[2(4k+3)-1]+[2(4k+2)-1)-[2(4k+1)-1]-[2\times 4k-1]=8\)，
故数列\(a_{4k}\)是等差数列，公差为\(8\)，首项为\(a_4\)，所以\(a_{4k}=a_4+(k-1)8\)；
同理，\(a_{4k+1}-a_{4k-3}=0\)，故数列\(\{a_{4k-3}\}\)是常数列，故\(a_{4k-3}=a_1\)；
\(a_{4k+3}-a_{4k-1}=0\)，故数列\(\{a_{4k-1}\}\)是常数列，故\(a_{4k-1}=a_3\)；
则数列\(b_{n+1}=a_{4n+1}+a_{4n+2}+a_{4n+3}+a_{4n+4}\)
\(=a_{4n-3}+a_{4n-2}+a_{4n-1}+a_{4n}+16=b_n+16\)， [9]
即\(b_{n+1}-b_n=16\)，又\(b_1=a_1+a_2+a_3+a_4=10\)，
则数列\(\{b_n\}\)是首项为\(10\)，公差为\(16\)的等差数列，
则则\(S_{60}=\cfrac{15[10+(16\times 15-6)]}{2}=1830\)；
研究函数性质
- [使用题目中的性质整合]已知\(f(x)+f(y)=f(xy)\)，在求解\(f(x)+f(2x-1)<f(3)\)时，需要将左端变形为\(f(x)+f(2x-1)=f[x(2x-1)]\)
- 拆分，研究函数\(f(x)=x+x^3\)的单调性和奇偶性时，如果拆分为\(y=x\)和\(y=x^3\)，由这两个组成部分函数的单调性和奇偶性就容易得到，函数\(f(x)\)为奇函数，且为\(R\)上的增函数；
- 拆分，研究函数\(f(x)=e^{1+|x|}-\cfrac{1}{1+x^2}\)的单调性和奇偶性时，如果拆分为\(y=e^{1+|x|}\)和\(y=-\cfrac{1}{1+x^2}\)，由这两个组成部分函数的单调性和奇偶性就容易得到，函数\(f(x)\)为偶函数，且在\((-\infty,0]\)上单调递减，在\([0,+\infty)\)上单调递增；
- 拆分，给定函数\(f(x)=asinx+b\sqrt[3]{x}+4\)，已知\(f(lg3)=3\)，求\(f(lg\cfrac{1}{3})\)时，如果能将函数变形为\(f(x)-4=asinx+b\sqrt[3]{x}\)，则可知函数\(f(x)-4\)为奇函数，就能容易求值。
- 函数作图中的拆分，如将函数 \(y=e^{2x}\) 拆分为 \(y={(e^2)}^x\) 就比 \(y=(e^x)^2\) 要好做图像，因为 函数 \(y={(e^2)}^x\) 是指数函数，属于基本初等函数，而 \(y=(e^x)^2\) 是个复合函数，是指数函数的平方，我们不太好想其中的细节。虽说\(e^{2x}={(e^2)}^x=({e^x})^2\)，此例能看出来思维的层次高低来。
导数法
- 用导数法判断函数的单调性时，比如\(f'(x)=(2e^x+a)\cdot (e^x-a)\)；
在作图时如果拆分为\(h(x)=2e^x+a\)和\(g(x)=e^x-a\)，在同一个坐标系中分别做出两个函数的图像，利用符号法则就可以知道\(f'(x)\)的正负，从而可知原函数\(f(x)\)的单调性；
- 已知函数\(f(x)=\cfrac{lnx+1}{e^x}\)，判断单调性；
\(f'(x)=\cfrac{\frac{1}{x}-lnx-1}{e^x}\)，将分子拆分为\(y=\cfrac{1}{x}-1\)和\(y=-lnx\)，其分界点为\(x=1\)。在同一个坐标系中分别做出两个函数的图像，利用符号法则就可以知道\(f'(x)\)的正负，从而可知原函数\(f(x)\)的单调性；
分析：将原函数拆分为两部分，令\(f(x)=x\cdot g(x)\)，\(g(x)=\)\((x-a_1)\)\((x-a_2)\)$\cdots $$(x-a_7)$，
则\(f'(x)=g(x)+x\cdot g'(x)\)，则\(f'(0)=g(0)+0\cdot g'(0)=g(0)\)，
\(g(0)=\)\((0-a_1)\)\((0-a_2)\)$\cdots $$(0-a_7)=-a_1\cdot a_2\cdots a_7=-a_4^7$①，
又由于各项均为正数的等比数列\(\{a_n\}\)，\(a_3\cdot a_5=2\)，则\(a_4^2=2\)，\(a_4=\sqrt{2}\)，
代入①式，得到\(f'(0)=g(0)=-8\sqrt{2}\)，故选\(B\)。
分析：由\(4\overrightarrow{AD}=\overrightarrow{AC}+3\overrightarrow{AB}\)，可得\(3\overrightarrow{AD}-3\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{AD}\)，
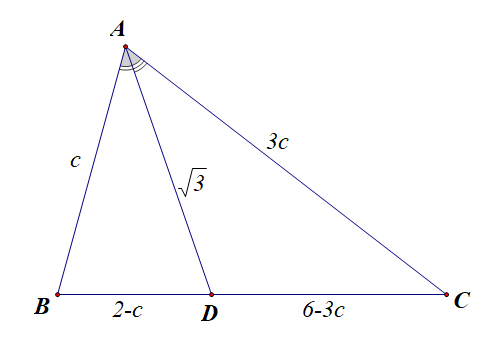
即\(3\overrightarrow{BD}=\overrightarrow{DC}\)，即\(|CD|=3|BD|\)，又\(4c+a=8\)，
则\(a=8-4c=|BC|\)，\(|BD|=\cfrac{1}{4}|BC|=2-c\)，\(|CD|=6-2c\)，
又由于\(AD\)为\(\angle BAC\)的平分线，由角平分线定理可知，
\(\cfrac{BD}{CD}=\cfrac{AB}{AC}=\cfrac{1}{3}\)，故\(|AC|=3c\)，
在\(\triangle ABD\)与\(\triangle ACD\)中，分别对\(\angle BAD\)和\(\angle DAC\)用余弦定理可得，
\(\cfrac{3+c^2-(2-c)^2}{2\times \sqrt{3}c}=\cfrac{3+(3c)^2-(6-3c)^2}{2\times \sqrt{3}\times 3c}\)
解得\(c=\cfrac{5}{4}\)，\(b=\cfrac{15}{4}\)，\(a=3\)。
解后反思：本题目需要特别注意向量系数的拆分技巧；
[解释：\(a_{(n+1)+1}+(-1)^{n+1}a_{n+1}=2(n+1)-1\)] ↩︎
对数列的下标详细说明如下，
所有正整数若除以\(4\)，就会分为四类，余数分别为\(0\)，\(1\)，\(2\)，\(3\)，
我们可以将其表达为\(4k\)，\(4k+1\)，\(4k+2\)，\(4k+3\)，此时\(k\in N\)；
还可以这样表达为\(4k-3\)，\(4k-2\)，\(4k-1\)，\(4k\)，此时\(k\in N^*\)；
故\(a_{4k-3}\)表达的是\(a_1\)，\(a_5\)，\(a_9\)，\(\cdots\)，
\(a_{4k-2}\)表达的是\(a_2\)，\(a_6\)，\(a_{10}\)，\(\cdots\)，
\(a_{4k-1}\)表达的是\(a_3\)，\(a_7\)，\(a_{11}\)，\(\cdots\)，
\(a_{4k}\)表达的是\(a_4\)，\(a_8\)，\(a_{12}\)，\(\cdots\)， ↩︎上述变形很有特点，这样变形的目的，既要保证恒等变形，还要充分利用上述的条件；
比如变形\((a_{4k}-a_{4k-1})\)意味着偶数项减去奇数项，即可以利用\(a_{n+1}-a_n=2n-1\)；
故有\((a_{4k}-a_{4k-1})=2(4k-1)-1\)，其余都同理； ↩︎由于下标的表示形式，故求和时只能从\(0\rightarrow 14\)，不能是\(1\rightarrow 15\)，否则求和会丢掉前面的四项而多算了后面的四项。 ↩︎
[此处用\(a_{4k+2}-a_{4k-2}\)，是为了求公差；由于前一项为\(a_{4k-2}\)，则其后一项为\(a_{4(k+1)-1}=a_{4k+2}\)；同时紧接着的变形既要保证恒等变形还要有效利用上述条件]； ↩︎
[此处用\(a_{4k+4}-a_{4k}\)，是为了求公差；由于前一项为\(a_{4k}\)，则其后一项为\(a_{4(k+1)}=a_{4k+4}\)；同时紧接着的变形既要保证恒等变形还要有效利用上述条件]； ↩︎
等差数列通项公式的拓展：\(a_n=a_m+(n-m)d\)；
此处可以这样理解，数列的公差为\(8\)，首项为\(a_4\)，自然能写出\(a_4+(k-1)8\)，关键是和\(a_{?}\)对应；
我们知道这个数列的首项应该是\(a_4\)，故下标应该用\(4k\)来表达，故\(a_{4k}=a_4+(k-1)8\)；
或者这样理解，从原来的母数列中间隔\(4\)项挑出来的项所组成的新数列的公差为\(8\)，那么回归到母数列里面，
相当于原来母数列的公差为\(2\)[当然母数列不是等差数列]，这样\(a_{4k}=a_4+(4k-4)\times 2=a_4+(k-1)8\)；
而不是\(a_{4k}=a_4+(4k-4)8\)；其他同理； ↩︎第二组子数列求和，首项是\(a_2\)，公差为\(8\)，项数为\(15\)项，故\(S_{2}=15a_2+\cfrac{15(15-1)}{2}\times 8=15a_2+840\). ↩︎
若\(b_{n+1}=a_{4n+1}+a_{4n+2}+a_{4n+3}+a_{4n+4}\)，用\(n-1\)替换左式中的\(n\)，
则得到\(b_{n}=a_{4n-3}+a_{4n-2}+a_{4n-1}+a_{4n}\)，故有\(b_{n+1}-b_n=16\)， ↩︎
