极坐标系相关 | 新高考已删
前言
为什么要引入极坐标呢?自然是觉得极坐标系有其自身表达上的优越性。
我们知道,通过直角坐标系,平面上的点与坐标(有序实数对)、曲线与方程建立了联系,从而实现了数与形的结合。根据几何对象的特征,选择适当的坐标系,建立它的方程,通过方程研究它的性质及与其他几何图形的关系,这就是研究几何问题的坐标法。
由于现实问题的复杂性,有时在直角坐标系下建立几何图形的方程并不方便。为便于用代数方法研究几何图形,需要建立不同的坐标系。在建立某些几何图形的方程时,用极坐标系、柱坐标系和球坐标系会更加方便。
比如涉及到某一个点\(P\),在直角坐标系下其表示为\(P(x,y)\),对应到极坐标系下表示为\(P(\rho,\theta)\),如果同时刻画距离\(|OP|\),则在直角坐标系下为\(|OP|=\sqrt{x^2+y^2}\),是二元根式函数问题,在极坐标系下为\(|OP|=\rho\),就是一元一次函数,相关的运算就简单的多了。[再比如学生上大学后在学习二重积分区域是圆的时候,直角坐标是要积分带根号的,运算难度比较大,而对于极坐标就不存在这样的问题.]
基础概念
在平面内取一个定点 \(O\) ,自点 \(O\) 引一条射线 \(Ox\) ,同时确定一个长度单位和计算角度的正方向 (通常取逆时针方向) ,这样就建立了一个极坐标系。点 \(O\) 称为极点,射线 \(Ox\) 称为极轴。平面内任一点 \(M\) 的位置可以由线段\(OM\)的长度 \(\rho\) 和从射线 \(Ox\) 到射线 \(OM\) 的角度 \(\theta\) 来刻画(如图所示)。
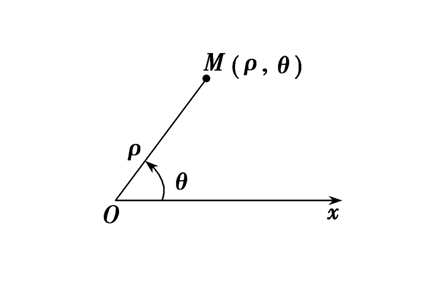
这两个数组成的有序数对 \((\rho,\theta)\) 称为点 \(M\) 的极坐标。\(\rho\) 称为点 \(M\) 的极径,\(\theta\) 称为点\(M\)的极角。一般认为\(\rho\geqslant 0\)特殊情况下,也容许\(\rho<0\),比如表述经过极点倾斜角为\(\cfrac{\pi}{3}\)的直线时,如果硬性规定\(\rho\)\(\geqslant\)\(0\),则直线只能用两条射线\(\theta\)\(=\)\(\cfrac{\pi}{3}\),且\(\rho\)\(\geqslant\)\(0\)和\(\theta\)\(=\)\(\cfrac{4\pi}{3}\),且\(\rho\)\(\geqslant\)\(0\) 来刻画,如果我们灵活规定,容许\(\rho\)\(<\)\(0\),且其含义刻画射线\(\theta\)\(=\)\(\cfrac{\pi}{3}\)的反向延长线上的点,则这条直线就可以简单的表述为\(\theta\)\(=\)\(\cfrac{\pi}{3}\),且\(\rho\)\(\in\)\(\R\)\(\quad\),当极角 \(\theta\) 的取值范围是 \([0,2\pi)\)时,平面上的点 (除去极点) 就与极坐标 \((\rho,\theta)\) 建立一一对应的关系。
我们规定,极点的极坐标中,极径 \(\rho=0\) ,极角 \(\theta\) 可取任意角,不过这也给我们造成了不小的困惑。
【易错警示】在极坐标系下,点的极坐标不唯一性易忽视,比如极坐标\((\rho,\theta)\) ,\((\rho,\theta+2k\pi)(k\in \Z)\), \((-\rho,\theta+\pi+2k\pi)(k\in \Z)\) 表示的是同一点的极坐标。
体会练习
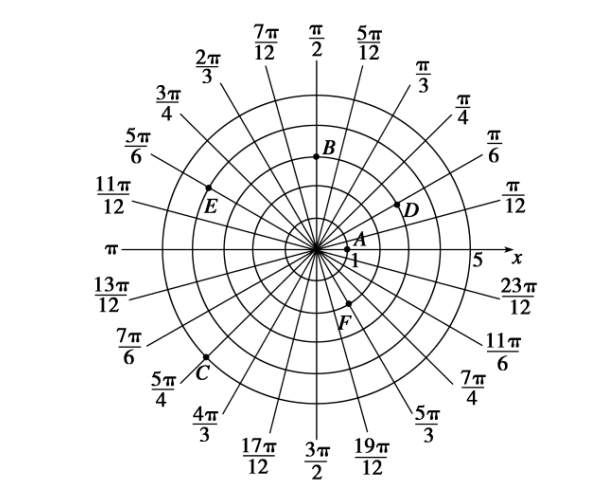
解后反思:知道点的极坐标 \((\rho,\theta)\) ,我们可以先根据极角 \(\theta\) 确定方向(射线),然后根据 \(\rho\) 来确定距离,进而描出 \((\rho,\theta)\) 的对应点.
常见方程表
| 曲线 | 图形 | 极坐标方程 |
|---|---|---|
| 圆心在极点,半径为\(r\)的圆 |  |
\(\rho=r\)\((0\leqslant\theta<2\pi)\) |
| 圆心在\((r,0)\),半径为\(r\)的圆 | 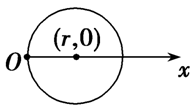 |
\(\rho=2r\cos\theta\)\((-\cfrac{\pi}{2}\leqslant\theta<\cfrac{\pi}{2})\) |
| 圆心在\((r,\cfrac{\pi}{2})\),半径为\(r\)的圆 | 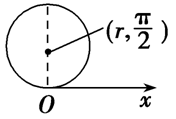 |
\(\rho=2r\sin\theta\)\((0\leqslant\theta<\pi)\) |
| 过极点,倾斜角为\(\alpha\)的直线 |  |
\(\theta=\alpha(\rho\in \R)\)或\(\theta=\pi+\alpha(\rho\in \R)\), 二者取一种即可 |
| 过点\((a,0)\),与极轴垂直的直线 |  |
\(\rho\cos\theta=a\)(\(-\cfrac{\pi}{2}<\theta<\cfrac{\pi}{2}\)) |
| 过点\((a,\cfrac{\pi}{2})\),与极轴平行的直线 | 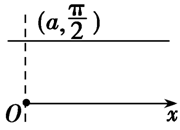 |
\(\rho\sin\theta=a\)(\(0<\theta<\pi\)) |
比较研究
- 平面直角坐标系下的直线和圆的方程
过原点的直线:\(y=kx\);
以\((0,0)\)为圆心,以\(2\)为半径的圆:\(x^2+y^2=2^2\)
以\((a,0)\)为圆心,以\(a\)为半径的圆:\((x-a)^2+y^2=a^2\)
以\((0,a)\)为圆心,以\(a\)为半径的圆:\(x^2+(y-a)^2=a^2\)
- 极坐标系下的直线和圆的方程
过原点的直线:\(\theta=\theta_0\);
以\((0,0)\)为圆心,以\(2\)为半径的圆:\(\rho=2\),\(\theta\in [-\pi,\pi]\);
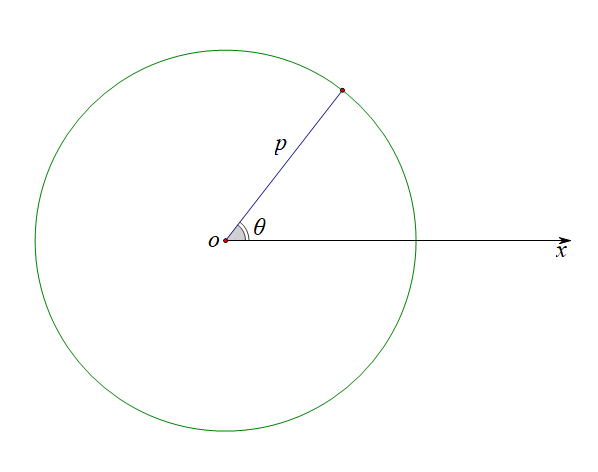
以\((a,0)\)为圆心,以\(a\)为半径的圆:\(\rho=2a cos\theta\),\(\theta\in [-\cfrac{\pi}{2},\cfrac{\pi}{2}]\);
推导用图形如下,
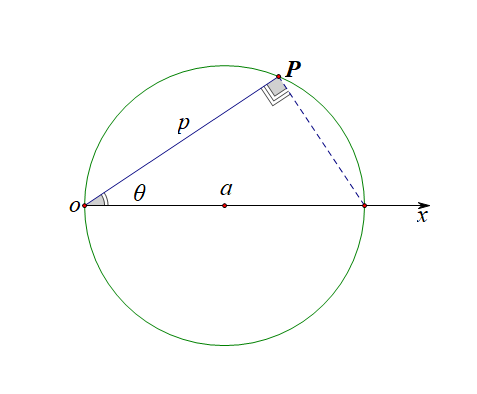
以\((a,\cfrac{\pi}{2})\)为圆心,以\(a\)为半径的圆:\(\rho=2a sin\theta\),\(\theta\in [0,\pi]\);
推导用图形如下,
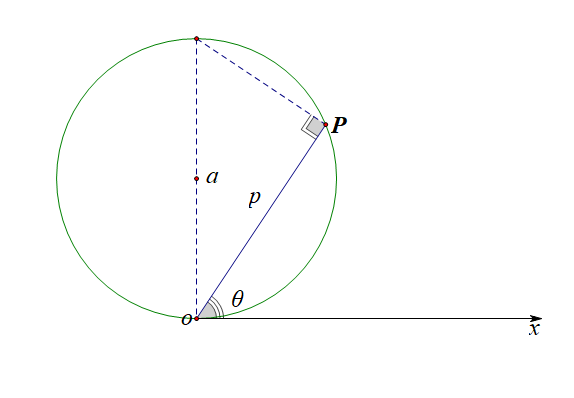
思路记录:由\(\rho=2a\cos\theta\),利用旋转\(\cfrac{\pi}{2}\)+相关点法,得到\(\rho=2a\sin\theta\);
由\(\rho=2a\cos\theta\),利用旋转\(\pi\)+相关点法,得到\(\rho=-2a\cos\theta\);
失误防范
- 涉及到极坐标的问题,以前的一般处理策略是将其转化到直角坐标系中来处理,下面的高考题目会让你体会到高考命题人的刁钻,以及直角坐标系的无奈。
(1).\(M\)为曲线\(C_1\)上的动点,点\(P\)在线段\(OM\)上,且满足\(|OM|\cdot|OP|=16\),求点\(P\)的轨迹\(C_2\)的直角坐标方程;
【法一】:学生容易想到的解法,也是我们交给学生的方法。
容易化简\(C_1:x=4\),做出简单的示意图,我们可以令\(M(4,m)、P(x,y)\),
则由题目可知\(\cfrac{y}{x}=\cfrac{m}{4}\),即\(m=\cfrac{4y}{x}\),
又由题目可知满足条件\(|OM|\cdot|OP|=16\),即\(\sqrt{4^2+m^2}\cdot\sqrt{x^2+y^2}=16\),
将\(m=\cfrac{4y}{x}\)代入,整理得到\((4^2+\cfrac{16y^2}{x^2})\cdot(x^2+y^2)=256\),
整理得到\(x^4+2x^2y^2-16x^2+y^4=0\),即\(x^4+2x^2y^2+y^4=16x^2\),
即\((x^2+y^2)^2=(4x)^2\),两边开方得到\(x^2+y^2=4x\)[此处由于\(x\)为非负值,故舍去\(x^2+y^2=-4x\)],
最终可以化简为\((x-2)^2+y^2=4(x>0)\)。
【法2】:直接借助极坐标系来思考运算,令\(M(\rho,\theta)\),\(P(\rho_1,\theta)(\rho_1>0)\),由题可知,
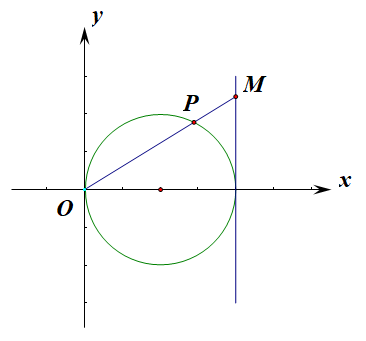
点M满足\(C_1\)的方程\(\rho cos\theta=4\) 。则\(\rho=\cfrac{4}{cos\theta}\),
又\(|OM|=\rho=\cfrac{4}{cos\theta}\),\(|OP|=\rho_1\),又由题目可知\(|OM|\cdot|OP|=\rho\rho_1=16\),
故\(\rho_1=\cfrac{16}{\rho}=4cos\theta(\rho_1>0)\),两边同乘以\(\rho_1\)得到
\(\rho_1^2=4\rho_1 cos\theta\),转化为直角坐标方程为\(x^2+y^2=4x(x\neq 0)\),
即\((x-2)^2+y^2=4(x\neq 0)\)为曲线\(C_2\)的直角坐标方程。
解后反思:
①法1的代数式变形,许多学生根本想不到;
②结题中限制\(x\neq 0\)是为了和上述的\(\rho_1>0\)对应。
③此题目的法2的解答提醒我们,若题目中出现了经过极点的两个线段的四则运算的条件,那么采用极坐标思考和运算应该是比较简单和快捷的,故我们必须扭转以直角坐标为桥梁的的求解思路,快速适应在极坐标系下的思维模式。
(2).设点\(A\)的极坐标为\((2,\cfrac{\pi}{3})\),点\(B\)在曲线\(C_2\)上,求\(\Delta OAB\)面积的最大值.
【法1】:直接借助平面几何的形来思考运算,结合运动观点和特殊化策略;让点\(B\)在圆上跑一圈即可看出思路;
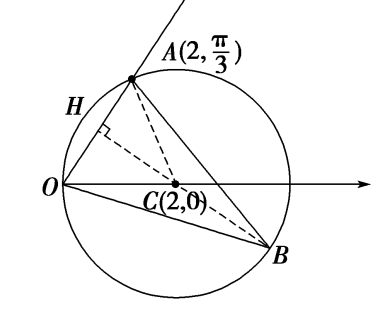
连接\(AC\) ,易知\(\Delta AOC\)为正三角形,底边\(|OA|\)为定值,则当高线最大时,\(S_{\Delta AOB}\)面积最大,
如图所示,过圆心\(C\)做\(AO\)的垂线,交\(AO\)于\(H\),交圆\(C\)于点\(B\),此时\(S_{\Delta AOB}\)面积最大,
\(S_{max}=\cfrac{1}{2}\cdot |AO||HB|=\cfrac{1}{2}\cdot |AO|(|HC|+|BC|)=2+\sqrt{3}\)。
【法2】:借助圆的参数方程和点线距公式求解;
直线\(OA\)的方程为\(\sqrt{3}x-y=0\),点\(B\)在曲线\(C_2\)上,
故点\(B\)的参数坐标为\((2cos\theta+2,2sin\theta)\)\((\theta\in (-\pi,\pi))\),
故三角形\(\Delta OAB\)的一条边\(OA\)上的高为点\(B\)到直线\(OA\)的距离为\(h_{OA}\),
\(h_{OA}=\cfrac{|\sqrt{3}(2cos\theta+2)-2sin\theta|}{\sqrt{(\sqrt{3})^2+1^2}}=|\sqrt{3}cos\theta-sin\theta+\sqrt{3}|\)
则\(S_{\Delta OAB}=\cfrac{1}{2}|OA|\cdot h_{OA}=|\sqrt{3}cos\theta-sin\theta+\sqrt{3}|=|2cos(\theta+\cfrac{\pi}{6})+\sqrt{3}|\),
当\(cos(\theta+\cfrac{\pi}{6})=1\),即\(\theta=-\cfrac{\pi}{6}\)时,\(S_{max}=2+\sqrt{3}\)。
【法3】:直接借助极坐标系来思考运算,利用\(S_{\triangle}=\cfrac{1}{2}absinC\)求解;
点\(A(2,\cfrac{\pi}{3})\),点\(B(\rho,\alpha)(\alpha\in (-\cfrac{\pi}{2},\cfrac{\pi}{2}))\),又点\(B\)满足曲线\(C_2\)的极坐标方程,
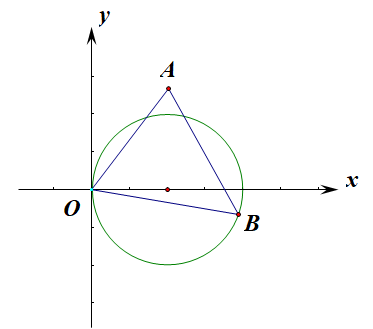
故\(|OB|=\rho=4cos\alpha\),\(\angle AOB=\cfrac{\pi}{3}-\alpha\),
则\(S_{\Delta OAB}=\cfrac{1}{2}|OA||OB|sin\angle AOB=\cfrac{1}{2}\cdot 2\cdot 4cos\alpha\cdot sin(\cfrac{\pi}{3}-\alpha)\)
\(=4cos\alpha \cdot sin(\cfrac{\pi}{3}-\alpha)=4cos\alpha\cdot(\cfrac{\sqrt{3}}{2}cos\alpha-\cfrac{1}{2}sin\alpha)\)
\(=2\sqrt{3}cos^2\alpha-2sin\alpha\cdot cos\alpha=\sqrt{3}\cdot (1+cos2\alpha)-sin2\alpha=-2sin(2\alpha-\cfrac{\pi}{3})+\sqrt{3}\),
故当\(2\alpha-\cfrac{\pi}{3}=-\cfrac{\pi}{2}\),即\(\alpha=-\cfrac{\pi}{12}\)时,\(S_{\Delta OAB}\)取到最大值\(2+\sqrt{3}\)。
典例剖析
(1)以坐标原点为极点,\(x\) 轴的正半轴为极轴建立极坐标系,求 \(C\) 的极坐标方程。
分析:由于极坐标方程中只有 \(\rho\) 和 \(\theta\),
故只要将\(x=\rho\cdot cos\theta\)和\(y=\rho\cdot sin\theta\)代入圆\(C\)的直角坐标方程为\((x+6)^2+y^2=25\),
整理可得\(\rho^2+12\rho cos\theta+11=0\)。
(2)直线 \(l\) 的参数方程为 \(\begin{cases} x=t\cdot cos\alpha \\ y=t\cdot sin\alpha \end{cases}(t为参数)\), \(l\) 与 \(C\) 交于 \(A\) 、 \(B\) 两点,\(|AB|=\sqrt{10}\),求直线 \(l\) 的斜率。
【法1】参数方程法,
分析:本题目的求解要用到直线的参数方程的几何意义。
将直线\(l\)的参数方程代入圆\(C\)的直角坐标方程,
化简整理为\(t^2+12t cos\alpha+11=0\),可设点\(A、B\)分别对应参数\(t_1,t_2\),
则\(\begin{cases} t_1+ t_2=-12cos\alpha \\ t_1\times t_2=11\end{cases}\),
\(|AB|=|t_1-t_2|= \sqrt{(t_1+t_2)^2-4t_1t_2}=\sqrt{10}\),
解得\(cos^2\alpha=\cfrac{54}{144}=\cfrac{3}{8}\),
又由图可知\(\alpha\in [0,\pi)\),故\(cos\alpha=\pm\cfrac{\sqrt{6}}{4}\),
则有\(sin\alpha=\cfrac{\sqrt{10}}{4}\)
故\(tan\alpha=\cfrac{sin\alpha}{cos\alpha}=\cfrac{\cfrac{\sqrt{10}}{4} }{\pm\cfrac{\sqrt{6}}{4}} =\pm\cfrac{\sqrt{15}}{3}\)。
故直线\(l\)的斜率为\(\pm\cfrac{\sqrt{15}}{3}\)。
【法2】极坐标系法,
圆\(C\)的极坐标方程是\(\rho^2+12\rho cos\theta+11=0\)。
将直线的参数方程两式相除得到,\(y=tan\alpha x\),即\(y=kx\),
则直线的极坐标方程为\(\theta=\alpha(\rho\in R)\)
将直线的极坐标方程代入圆\(C\)的极坐标方程是\(\rho^2+12\rho cos\theta+11=0\),
得到圆\(C\)的极坐标方程是\(\rho^2+12\rho cos\alpha+11=0\),
设点\(A\)的极坐标方程为\((\rho_1,\alpha)\),点\(B\)的极坐标方程为\((\rho_2,\alpha)\),
则\(\rho_1+\rho_2=-12cos\alpha\),\(\rho_1\cdot \rho_2=11\),
由\(|AB|=|\rho_1-\rho_2|= \sqrt{(\rho_1+\rho_2)^2-4\rho_1\rho_2}=\sqrt{10}\),
解得\(cos^2\alpha=\cfrac{54}{144}=\cfrac{3}{8}\),
又由图可知\(\alpha\in [0,\pi)\),故\(cos\alpha=\pm\cfrac{\sqrt{6}}{4}\),
则有\(sin\alpha=\cfrac{\sqrt{10}}{4}\)
故\(tan\alpha=\cfrac{sin\alpha}{cos\alpha}=\cfrac{\cfrac{\sqrt{10}}{4} }{\pm\cfrac{\sqrt{6}}{4}} =\pm\cfrac{\sqrt{15}}{3}\)。
故直线\(l\)的斜率为\(\pm\cfrac{\sqrt{15}}{3}\)。
【法3】平面几何法,如图所示,这样的直线应该有两条,且其斜率互为相反数,现重点求解图中的直线\(AB\)的斜率,
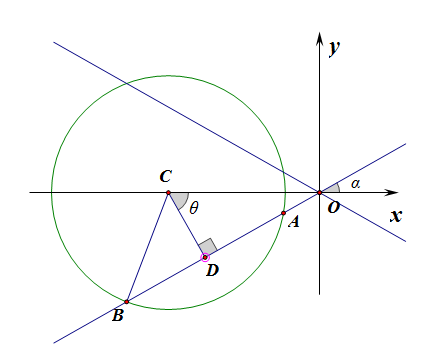
在\(Rt\Delta BCD\)中,半径为\(BC=5\),半弦长为\(BD=\cfrac{\sqrt{10}}{2}\),
利用勾股定理求得,弦心距\(CD=\cfrac{3\sqrt{10}}{2}\)
在\(Rt\Delta OCD\)中,\(OC=6\),\(CD=\cfrac{3\sqrt{10}}{2}\)
求得\(cos\angle OCD=cos\theta=\cfrac{\sqrt{10}}{4}\)
从而\(sin\alpha=\cfrac{\sqrt{10}}{4}\),\(cos\alpha=\cfrac{\sqrt{6}}{4}\),
即\(k=tan\alpha=\cfrac{\sqrt{10}}{\sqrt{6}}=\cfrac{\sqrt{15}}{3}\),
故满足条件的直线\(AB\)有两条,其斜率为\(\pm\cfrac{\sqrt{15}}{3}\)。
(1).当\(\theta_0=\cfrac{\pi}{3}\)时,求\(\rho_0\)及\(l\)的极坐标方程;
分析:当\(\theta_0=\cfrac{\pi}{3}\)时,由\(\rho=4sin\theta\),得到\(\rho_0=4sin\cfrac{\pi}{3}=2\sqrt{3}\);
求直线\(l\)的极坐标方程有以下两个思路,可以比较看,哪一种更简便。
思路1:过点\(A\)的直线\(l\)的斜率为\(k=-\cfrac{1}{tan\frac{\pi}{3}}=-\cfrac{\sqrt{3}}{3}\),
故直线\(l\)的普通方程为\(y-0=-\cfrac{\sqrt{3}}{3}(x-4)\),
再用\(y=\rho\cdot sin\theta\)和\(x=\rho\cdot cos\theta\)代入上式,
变形直线的极坐标方程为\(\sqrt{3}\rho cos\theta+3\rho sin\theta=4\sqrt{3}\),整理为
\(\rho\cdot sin(\theta+\cfrac{\pi}{6})=2\)或者\(\rho\cdot cos(\theta-\cfrac{\pi}{3})=2\)
思路2:如图所示,在极坐标系下直接思考和运算,
在\(\triangle OAP\)中,已知\(OA=4\),\(\angle PAO=\cfrac{\pi}{6}\),则\(OP=2\),
在直线\(l\)上任取一点\(B(\rho,\theta)\),则在\(\triangle OPB\)中,已知\(OB=\rho\),\(\angle POB=\cfrac{\pi}{3}-\theta\),\(OP=2\),
则\(\rho\cdot cos(\cfrac{\pi}{3}-\theta)=2\),也即\(\rho\cdot cos(\theta-\cfrac{\pi}{3})=2\)
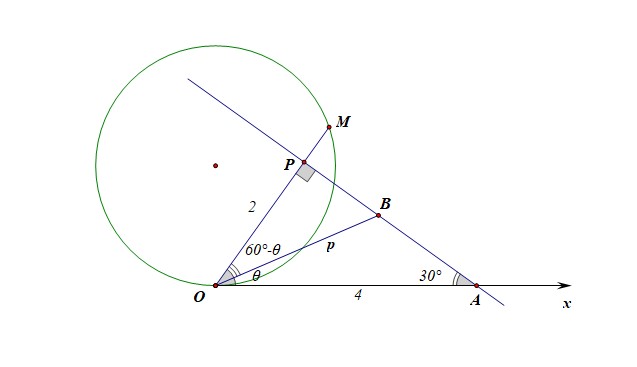
解后反思:相比较而言,在极坐标系下求直线的方程,我们只需要借助解三角形就可以搞定了,原因是在极坐标系下\(\rho\)的含义一定是极点到动点的线段的长度,这样就可以顺利借助解三角形来完成了。
(2).当\(M\)在\(C\)上运动且\(P\)在线段\(OM\)上时,求\(P\)点轨迹的极坐标方程。
分析:同样的,求\(P\)点轨迹的极坐标方程,我们也可以有两个思路来考虑,
思路1:在直角坐标系下思考求解,然后转化划归。
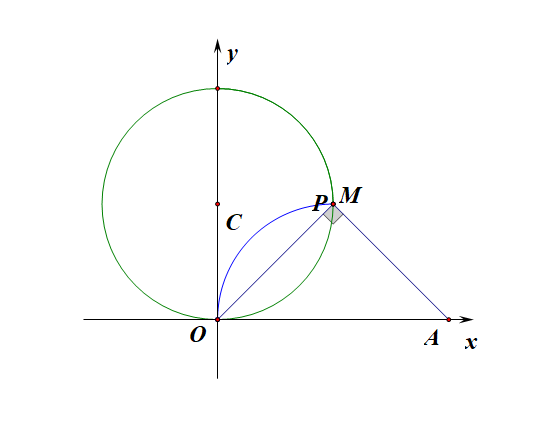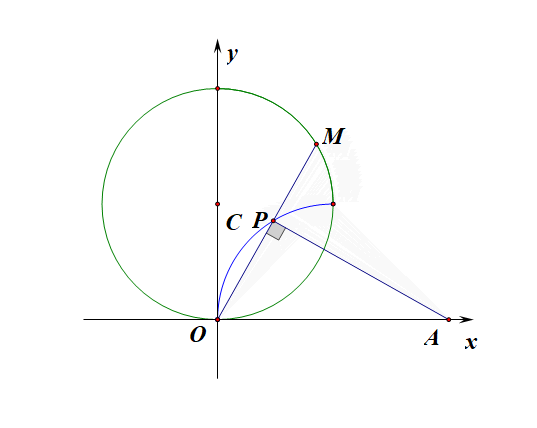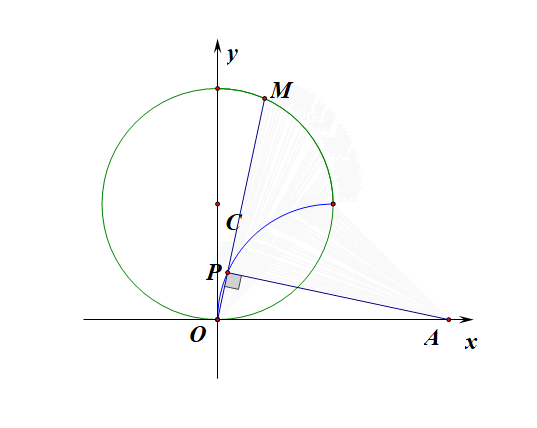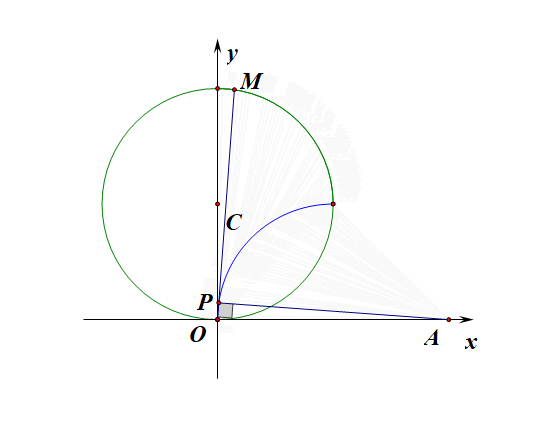
设直线\(OM:y=kx\),则直线\(AP:y=-\cfrac{1}{k}(x-4)\),
则两条直线的交点\(P\)的参数方程为\(\left\{\begin{array}{l}{y=kx①}\\{y=-\cfrac{1}{k}(x-4)②}\end{array}\right.(k为参数,k\geqslant 1)\),
两式相乘,消去参数,得到\(y^2=-x(x-4)\),
即\(x^2+y^2-4x=0\),转化为极坐标方程为\(\rho^2=4\rho cos\theta\),
即\(\rho=4cos\theta\),对应的\(\theta\in [\cfrac{\pi}{4},\cfrac{\pi}{2})\),
再思考当\(k\)不存在时,点\(P\)落在原点,也满足题意,对应\(\theta=\cfrac{\pi}{2}\),
综上所述,\(P\)点轨迹的极坐标方程为\(\rho=4cos\theta\),\(\theta\in [\cfrac{\pi}{4},\cfrac{\pi}{2}]\),
思路2:如图所示,在极坐标系下直接思考和运算,
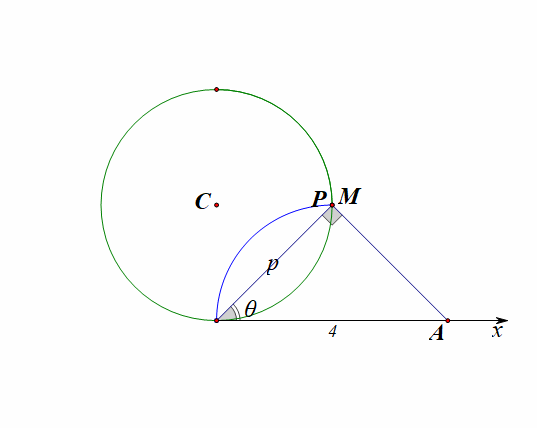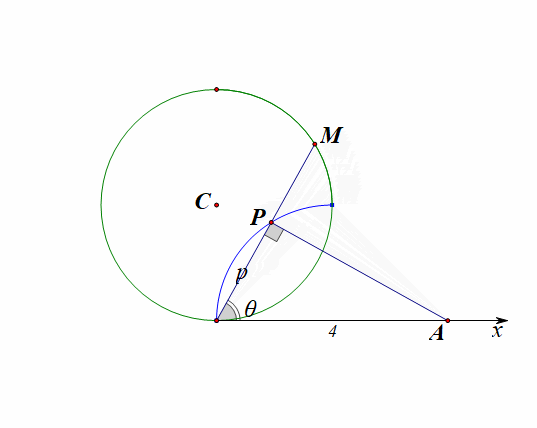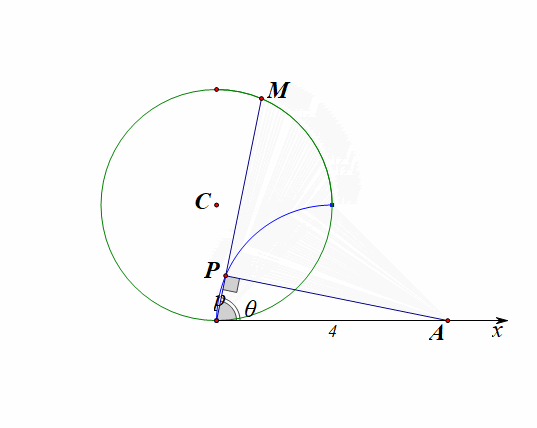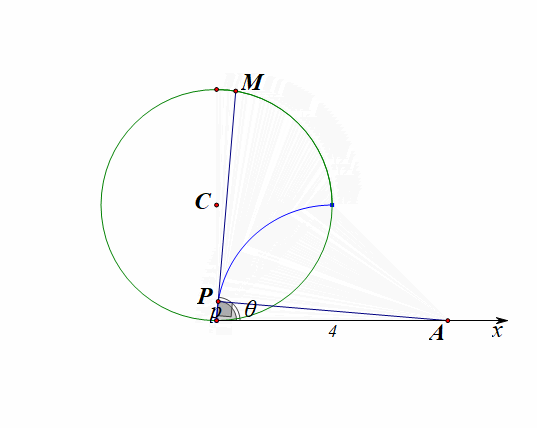
设动点\(P(\rho,\theta)\),在\(\angle OAP\)中,\(OP=\rho\),我们很容易得到\(cos\theta=\cfrac{\rho}{4}\),
即\(\rho=4cos\theta\),且\(\theta\in [\cfrac{\pi}{4},\cfrac{\pi}{2}]\),
故\(P\)点轨迹的极坐标方程为\(\rho=4cos\theta\),\(\theta\in [\cfrac{\pi}{4},\cfrac{\pi}{2}]\)。
解后反思:由这两小问题的解答过程比较分析,同样的问题,当放到极坐标下思考和运算会变得很简单,之所以我们感觉难,是因为我们对极坐标系很不熟悉而已。
(1)写出曲线\(C_1\)的普通方程和\(C_2\)的直角坐标方程;
分析:(1) 直接给出答案,
曲线的普通方程\(C_1:(x-2)^2+y^2=4\);
所求的直角坐标方程\(C_2:(x-1)^2+y^2=1\);
(2)设点\(P\) 在\(C_1\)上,点\(Q\) 在\(C_2\)上,且\(\angle POQ=\cfrac{\pi}{2}\),求三角形\(POQ\)面积的最大值。
分析:【法1】极坐标法(本题目命题意图就是想让学生体会极坐标的优越性,从而主动使用极坐标刻画思考或者在极坐标系下运算),
曲线\(C_1\)的极坐标方程为\(\rho_1=4cos\alpha(\alpha\in(-\cfrac{\pi}{2},\cfrac{\pi}{2}))\),
曲线\(C_2\)的极坐标方程为\(\rho_2=2cos\theta(\theta\in(-\cfrac{\pi}{2},\cfrac{\pi}{2}))\),
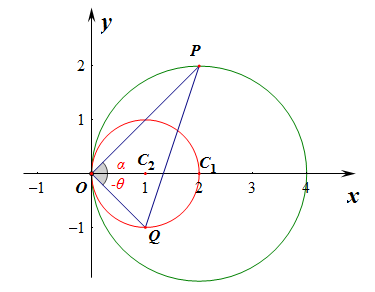
如图所示,初步分析,当点\(P\)在\(x\)轴上方时,点\(Q\)必在\(x\)轴下方;
当然还会有另一种情形,当点\(P\)在\(x\)轴下方时,点\(Q\)必在\(x\)轴上方;
我们取其中一种做研究,比如点\(P\)在\(x\)轴上方,点\(Q\)在\(x\)轴下方;
注意此时点\(Q\)的极角是负值\(-\theta\),
由于\(\rho_1>0\),\(\rho_2>0\),以及\(\angle POQ=\cfrac{\pi}{2}\)可得,
\(\alpha-\theta=\cfrac{\pi}{2}\),即\(\alpha=\theta+\cfrac{\pi}{2}\),(顺时针为正,逆时针为负)
则有\(S_{\Delta OPQ}=\cfrac{1}{2}|OP||OQ|\)
\(=\cfrac{1}{2}\rho_1\rho_2=\cfrac{1}{2}\times 4cos\alpha\times 2cos\theta\)
\(=4cos(\theta+\cfrac{\pi}{2})cos\theta=-4sin\theta cos\theta\)
\(=-2sin2\theta\),
当\(2\theta=-\cfrac{\pi}{2}\),即\(\theta=-\cfrac{\pi}{4}\)时,
\((S_{\Delta OPQ})_{max}=2\)。
【法2】参数方程法,
如图所示,曲线\(C_1\)的参数方程是\(\begin{cases}x=2+2cos\alpha\\y=2sin\alpha\end{cases}(\alpha为参数,\alpha\in (-\pi,\pi))\),
曲线\(C_2\)的参数方程是\(\begin{cases}x=1+cos\theta\\y=sin\theta\end{cases}(\theta为参数,\theta\in (-\pi,\pi))\),
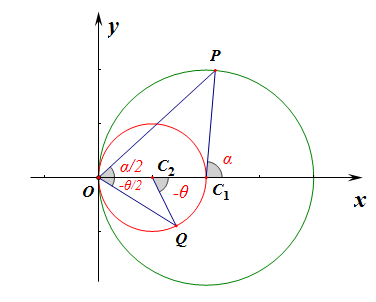
注意参数的含义,\(\cfrac{\alpha}{2}-\cfrac{\theta}{2}=\cfrac{\pi}{2}\),即\(\alpha=\pi+\theta\)
则有\(S_{\Delta OPQ}=\cfrac{1}{2}|OP||OQ|\)
\(=\cfrac{1}{2}\sqrt{(2+2cos\alpha)^2+(2sin\alpha)^2}\sqrt{(1+cos\theta)^2+sin^2\theta}\)
\(=\cfrac{1}{2}\sqrt{8(1+cos\alpha)}\sqrt{2(1+cos\theta)}\)
\(=\cfrac{1}{2}\sqrt{8(1-cos\theta)}\sqrt{2(1+cos\theta)}\)
\(=\cfrac{1}{2}\times 4\sqrt{(1-cos\theta)(1+cos\theta)}\)
\(=2\sqrt{1-cos^2\theta}=2|sin\theta|\)
当\(\theta=-\cfrac{\pi}{2}\)时,\((S_{\Delta OPQ})_{max}=2\)。
【变形方法3】参数方程法,曲线\(C_1\)的参数方程是\(\begin{cases}x=2+2cos\alpha\\y=2sin\alpha\end{cases}(\alpha为参数,\alpha\in (-\pi,\pi))\),
曲线\(C_2\)的参数方程是\(\begin{cases}x=1+cos\theta\\y=2sin\theta\end{cases}(\theta为参数,\theta\in (-\pi,\pi))\),
注意参数的含义,\(\cfrac{\alpha}{2}-\cfrac{\theta}{2}=\cfrac{\pi}{2}\),即\(\alpha=\pi+\theta\)
由\(\angle POQ=\cfrac{\pi}{2}\)可知,\(k_{OP}k_{OQ}=-1\),
即\(\cfrac{2sin\alpha}{2+2cos\alpha}\times \cfrac{sin\theta}{1+cos\theta}=-1\),即\(-sin\alpha sin\theta=(1+cos\alpha)(1+cos\theta)\)
\(S_{\Delta OPQ}=\cfrac{1}{2}|OP||OQ|\)
\(=\cfrac{1}{2}\sqrt{(2+2cos\alpha)^2+(2sin\alpha)^2}\sqrt{(1+cos\theta)^2+sin^2\theta}\)
\(=\cfrac{1}{2}\sqrt{8(1+cos\alpha)}\sqrt{2(1+cos\theta)}\)
\(=2\sqrt{(1+cos\alpha)(1+cos\theta)}\)
\(=2\sqrt{-sin\alpha sin\theta}\),
又有\(\cfrac{\alpha}{2}-\cfrac{\theta}{2}=\cfrac{\pi}{2}\),即\(\alpha=\pi+\theta\)
\(原式=2\sqrt{sin^2\theta}=2|sin\theta|\),
当\(\theta=-\cfrac{\pi}{2}\)时,\((S_{\Delta OPQ})_{max}=2\)。
【法4】尝试使用均值不等式,待有空思考整理。
设直线\(OP\)的方程为\(y=kx\),由\(\angle POQ=\cfrac{\pi}{2}\)可得,
直线\(OQ\)的方程为\(y=-\cfrac{1}{k}x\),
联立\(\begin{cases}(x-2)^2+y^2=4\\y=kx\end{cases}\),
解得\(P(\cfrac{4}{1+k^2},\cfrac{4k}{1+k^2} )\),
联立\(\begin{cases}(x-1)^2+y^2=1\\y=-\cfrac{1}{k}x\end{cases}\),
解得\(Q(\cfrac{2k^2}{1+k^2},\cfrac{-2k}{1+k^2} )\),
\(S_{\Delta POQ}=\cfrac{1}{2}|OP||OQ|=\cfrac{1}{2}\sqrt{(\cfrac{4}{1+k^2})^2+(\cfrac{4k}{1+k^2})^2}\sqrt{(\cfrac{2k^2}{1+k^2})^2+(\cfrac{-2k}{1+k^2})^2}\)
\(=\cfrac{1}{2}\sqrt{\cfrac{16}{1+k^2}}\sqrt{\cfrac{4k^2}{1+k^2}}=\cfrac{4|k|}{1+k^2}=\cfrac{4}{|k|+\frac{1}{|k|}}\leq 2\)。
当且仅当\(|k|=1\)时取到等号。故\((S_{\Delta POQ})_{max}=2\)。
反思:这个解法的优越性体现在只有一个变量\(k\),那么求最值时就好操作些。
【法5】是否有,待后思考整理。
解后反思:
1、在高中数学中,求某个量(比如面积)的最值时,往往需要先表达出这个量(比如面积)的函数,这样求实际问题的最值就变成了求这个函数模型的最值问题了,这一过程实际就是函数的建模。
1、法1利用极坐标法,这样表达刻画面积时,就只有两个变量\(\alpha\)和\(\theta\),然后利用两个变量的相互关系,再将变量集中为一个变量,就好求解其最大值了。
2、法2利用参数方程法,在表达刻画面积时,同样只有两个变量\(\alpha\)和\(\theta\),然后利用两个变量的相互关系,再将变量集中为一个变量,就好求解其最大值了。法2和法3本质接近。
3、正确求解本题目,需要深刻理解极坐标方程的含义和参数方程的含义,尤其是法2对参数的含义更不能弄错了。用到了内外角关系和圆心角和圆周角关系。
4、还有学生想到设\(P(x_1,y_1)\),$ Q(x_2,y_2)$,这样的思路我没有做尝试,不过能看出来此时是四个变量,这样就难得多了,所以碰到这样的题目我们先需要初步筛选思路。
(1)求线段\(AD\)的中点\(M\)的轨迹\(E\)的普通方程。
分析:点\(D\)的直角坐标为\((-2,-2\sqrt{3})\),(计算方法:\(x=\rho\cdot cos\theta\)等),由题意可设\(A\)的坐标为\((2cos\alpha,sin\alpha)\),
则\(AD\)的中点\(M\)的坐标为\((-1+cos\alpha,-\sqrt{3}+\cfrac{1}{2}sin\alpha)\),
所以\(M\)的轨迹\(E\)的参数方程为\(\left\{\begin{array}{l}{x=-1+cos\alpha}\\{y=-\sqrt{3}+\cfrac{1}{2}sin\alpha}\end{array}\right.(\alpha为参数)\),
消参得到,轨迹\(E\)的普通方程为\((x+1)^2+4(y+\sqrt{3})^2=1\)。
(2)利用椭圆\(C\)的极坐标方程证明\(\cfrac{1}{|OA|^2}+\cfrac{1}{|OB|^2}\)为定值,并求\(\Delta ABC\)面积的最大值。
分析:椭圆\(C\)的普通方程为\(\cfrac{x^2}{4}+y^2=1\),
化为极坐标方程为\(\rho^2+3\rho^2sin^2\theta=4\),
变形得到,\(\rho^2=\cfrac{4}{1+3sin^2\theta}\),\(\rho=\cfrac{2}{\sqrt{1+3sin^2\theta}}\),
由\(OA\perp OB\),可设\(A(\rho_1,\theta)\),\(B(\rho_2,\theta+\cfrac{\pi}{2})\),
所以\(\cfrac{1}{|OA|^2}+\cfrac{1}{|OB|^2}\)
\(=\cfrac{1}{\rho_1^2}+\cfrac{1}{\rho_2^2}\)
\(=\cfrac{1+3sin^2\theta}{4}+\cfrac{1+3sin^2(\theta+\frac{\pi}{2})}{4}\)
\(=\cfrac{2+3sin^2\theta+3cos^2\theta}{4}=\cfrac{5}{4}\),(定值)。
\(S_{\Delta AOB}=\cfrac{1}{2}\rho_1\rho_2=\cfrac{1}{2}\cdot \cfrac{2}{\sqrt{1+3sin^2\theta}}\cdot \cfrac{2}{\sqrt{1+3cos^2\theta}}\)
\(=\cfrac{2}{\sqrt{(1+3sin^2\theta)(1+3cos^2\theta)}}\)
\(=\cfrac{2}{\sqrt{1+3+9sin^2\theta cos^2\theta}}\)
\(=\cfrac{2}{\sqrt{4+\cfrac{9}{4}sin^22\theta}}\),
当\(sin2\theta=0\)时,\(S_{\Delta AOB}\)的最大值为\(1\)。
(1)求直线\(l\)被曲线\(C\)截得的弦长\(|OA|\).
分析:可以从以下四个角度思考,
①利用两点间的距离公式;
【法1】直线\(l\)的普通方程为\(y=\sqrt{3}x\),圆\(C\)的普通方程为\(x^2+(y-2)^2=2^2\),
联立消掉\(y\),得到\(x^2-\sqrt{3}x=0\),
解得,\(\left\{\begin{array}{l}{x_1=0}\\{y_1=0}\end{array}\right.\),或\(\left\{\begin{array}{l}{x_2=\sqrt{3}}\\{y_2=3}\end{array}\right.\),
由两点间距离公式得到\(|OA|=2\sqrt{3}\)。
②直线和圆相交求弦长的几何方法;
【法2】直线为\(\sqrt{3}x-y=0\),圆心为\((0,2)\),
则圆心到直线的距离为\(d=\cfrac{|0-2|}{2}=1\),又半径为\(2\),
故半弦长为\(\sqrt{2^2-1^2}=\sqrt{3}\),则弦长\(|OA|=2\sqrt{3}\)。
③直线的参数方程法;
【法3】由于直线的普通方程为\(y=\sqrt{3}x\),
经过点\((0,0)\),斜率\(k=tan\theta=\sqrt{3}\),
直线\(l\)的参数方程为\(\left\{\begin{array}{l}{x=0+\cfrac{1}{2}t}\\{y=0+\cfrac{\sqrt{3}}{2}t}\end{array}\right.(t为参数)\),
将其代入圆的普通方程\(x^2+(y-2)^2=2^2\),
整理得到\(t^2-2\sqrt{3}t=0\),
解得\(t_1=0\),\(t_2=2\sqrt{3}\),
则弦长\(|OA|=|t_1-t_2|=2\sqrt{3}\)。
④极坐标法;
【法4】直线的极坐标方程为\(\theta=\cfrac{\pi}{3}\),
圆的极坐标方程为\(\rho=4sin\theta\),
二者联立,得到\(\rho=4sin\cfrac{\pi}{3}=2\sqrt{3}\)。
即所求弦长\(|OA|=2\sqrt{3}\)。
(2)从极点做曲线\(C\)的弦,求弦的中点\(M\)轨迹的极坐标方程。
分析:可以从以下三个角度思考:
①利用平面直角坐标系下的中点公式;
【法1】相关点法,在平面直角坐标系中,设过坐标原点的直线和圆相交于点\(P(x_0,y_0)\),则所得弦的中点坐标为\(M(x,y)\)
则\(\left\{\begin{array}{l}{2x=x_0}\\{2y=y_0}\end{array}\right.\),又点\(P(x_0,y_0)\)在圆\(x^2+(y-2)^2=2^2\)上,
代入整理得到普通方程为\(x^2+(y-1)^2=1\),
即其极坐标方程为\(\rho=2sin\theta\),
其中\(\alpha\in(0,\pi)\),而不是\(\alpha\in[0,\pi)\),以保证弦的存在。
②利用圆的参数方程;
由于圆上任意一动点\(P\)的坐标\(P(2cos\theta,2+2sin\theta)\),则弦的中点\(M(cos\theta,1+sin\theta)\),
即点\(M\)的参数方程为\(\left\{\begin{array}{l}{x=cos\theta}\\{y=1+sin\theta}\end{array}\right.(\theta为参数)\),
消去参数\(\theta\),得到普通方程为\(x^2+(y-1)^2=1\),
即其极坐标方程为\(\rho=2sin\theta\),
其中\(\alpha\in(0,\pi)\),而不是\(\alpha\in[0,\pi)\),以保证弦的存在。
③利用极坐标法;
【法3】曲线\(C\)的极坐标方程为\(\rho=4sin\theta\),
过极点的直线的极坐标方程为\(\theta=\alpha\),
设直线和曲线\(C\)的交点的极坐标为\((\rho_1,\alpha)\),
则弦的中点\(M\)的极坐标为\((\rho,\alpha)\),
由题目可知,\(\rho_1=2\rho\),代入曲线\(C\)的极坐标方程为\(2\rho=4sin\alpha\),
得到\(\rho=2sin\alpha\),其中\(\alpha\in(0,\pi)\)。
故弦的中点\(M\)轨迹的极坐标方程为\(\rho=2sin\alpha\),其中\(\alpha\in(0,\pi)\)。
说明:由于弦的中点要存在,则必须保证\(\rho\neq 0\),即原来的\(\alpha\in[0,\pi)\),必须变为\(\alpha\in(0,\pi)\)。
(1).求直线 \(l\) 的极坐标方程及曲线 \(C\) 的直角坐标方程
分析:直线 \(l\) 的参数方程为 \(\left\{\begin{array}{l}{x=\sqrt{3}+\cfrac{1}{2}t}\\{y=1+\cfrac{\sqrt{3}}{2}t}\end{array}\right.\),
消参后转换为直角坐标方程为 \(y-1=\sqrt{3}(x-\sqrt{3})\),整理得 \(\sqrt{3} x-y-2=0\),
转换为极坐标方程为 \(\sqrt{3} \rho \cos \theta-\rho \sin \theta-2=0\).
曲线 \(C\) 的极坐标方程为\(\rho=2 \cos \theta\),整理得 \(\rho^{2}=2 \rho \cos \theta\),
转换为直角坐标方程 \(x^{2}+y^{2}=2 x\), 即 \(x^{2}+y^{2}-2x=0\);
(2). 若 \(A(\rho_{1}, \alpha)\) 是直线 \(l\) 上一点, \(B(\rho_{2}, \alpha-\cfrac{\pi}{3})\) 是曲线 \(C\) 上一点, 求 \(\cfrac{|OB|}{|OA|}\) 的最大值.
分析:由于 \(A(\rho_{1}, \alpha)\) 是直线 \(l\) 上一点,, 则 \(\sqrt{3}\rho_{1}\cos\alpha-\rho_{1}\sin\alpha-2=0\), 则\(\rho_1=\cfrac{2}{\sqrt{3}\cos\alpha-\sin\alpha}\),
\(B(\rho_{2}, \alpha-\cfrac{\pi}{3})\) 是曲线 \(C\) 上一点,则: \(\rho_{2}=2\cos(\alpha-\cfrac{\pi}{3})\),
\(\cfrac{|OB|}{|OA|}=\cfrac{\rho_{2}}{\rho_{1}}=(\cfrac{1}{2}\cos\alpha+\cfrac{\sqrt{3}}{2}\sin \alpha)(\sqrt{3}\cos\alpha-\sin\alpha)\)
\(=\cfrac{1}{2}(\sqrt{3}\cos^{2}\alpha+2\sin\alpha\cos\alpha-\sqrt{3}\sin^{2}\alpha)\)
\(=\sin(2\alpha+\cfrac{\pi}{3})\leqslant 1\),
故 \(\cfrac{|OB|}{|OA|}\) 的最大值为 \(1\).
解析: 极坐标系中两点 \(A\left(\rho_{1}, \theta_{1}\right)\), \(B\left(\rho_{2}, \theta_{2}\right)\) 的距离公式为 \(|AB|=\sqrt{\rho_{1}^{2}+\rho_{2}^{2}-2 \rho_{1} \rho_{2} \cos \left(\theta_{1}-\theta_{2}\right)}\),
代入相关数值计算,得到 \(|AB|=\cfrac{3\sqrt{6}+3\sqrt{2}}{2}\), 故答案为 \(C\) .
(1). 求曲线 \(C_1\) 的极坐标方程;
解析:本题目依托 \((\cfrac{2t}{1+t^2})^2+(\cfrac{1-t^2}{1+t^2})^2=1\) 来消参。
由于 \(y=\cfrac{3+2t^2}{1+2t^2}=2+\cfrac{1-2t^2}{1+2t^2}\),则有 \(y-2=\cfrac{1-2t^2}{1+2t^2}\),
所以 \(x^2+(y-2)^2=(\cfrac{2\sqrt{2}t}{1+2t^2})^2+(\cfrac{1-2t^2}{1+2t^2})^2=1\),
因为 \(C_1\) 可化为 \(x^2+y^2-4y+3=0\)(\(y\neq1\)),所以曲线 \(C_1\) 的极坐标方程为 \(\rho^2-4\rho\sin\theta+3=0\)(\(\rho\neq1\))。
(2). 曲线 \(C_3\) 与曲线 \(C_1\) 交于 \(A\),\(B\) 两点,与曲线 \(C_2\) 交于点 \(C\) ,若\(|OC|=\cfrac{15}{16}(|OA|+|OB|)\),求 \(a\) 的值。
解析:由于曲线 \(C_3\) 与曲线 \(C_1\) 交于 \(A\),\(B\) 两点,则点 \(A\),\(B\) 同时满足两条曲线的方程,
令 \(A(\rho_{_A},\theta)\),\(B(\rho_{_B},\theta)\) 故联立得到\(\left\{\begin{array}{l}\theta=\alpha\\\rho^2-4\rho\sin\theta+3=0\end{array}\right.\)
将 \(\theta=\alpha\) 代入消元 \(\theta\) ,得到 \(\rho^2-4\rho\sin\alpha+3=0\),
又由于 \(\tan\alpha=2\),则可知 \(\sin\alpha=\cfrac{2\sqrt{5}}{5}\),代入上式得到,\(\rho^2-\cfrac{8\sqrt{5}}{5}\rho+3=0\),
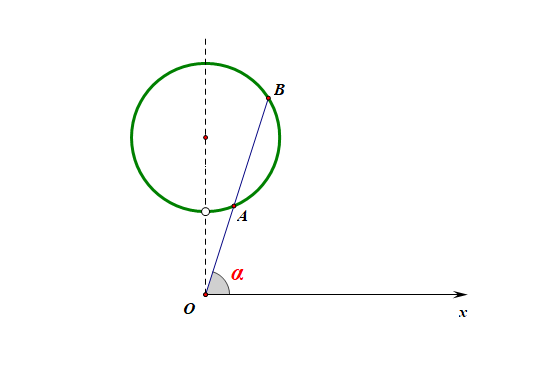
又由上可知,\(\rho_{_A}\), \(\rho_{_B}\) 是方程的两个根,故有 \(|OA|+|OB|=\rho_{_A}+\rho_{_B}=\cfrac{8\sqrt{5}}{5}\),
故有 \(|OC|=\cfrac{15}{16}(|OA|+|OB|)=\cfrac{15}{16}\times \cfrac{8\sqrt{5}}{5}=\cfrac{3\sqrt{5}}{2}\).
同理,如图所示,曲线 \(C_3\) 与曲线 \(C_2\) 交于点 \(C(\rho_{_C},\theta)\) ,则点 \(C\) 同时满足两条曲线的方程,

联立得到\(\left\{\begin{array}{l}\theta=\alpha\\\rho\sin\theta+2\rho\cos\theta-a=0\end{array}\right.\) ,将 \(\theta=\alpha\) 代入消元 \(\theta\) ,
得到 \(\rho\sin\alpha+2\rho\cos\alpha-a=0\),由 \(\tan\alpha=2\),则可知 \(\sin\alpha=\cfrac{2\sqrt{5}}{5}\),且 \(\cos\alpha=\cfrac{\sqrt{5}}{5}\),
代入整理得到,\(\rho\times \cfrac{2\sqrt{5}}{5}+\rho\times \cfrac{2\sqrt{5}}{5}-a=0\),即 \(\rho=\cfrac{a}{\frac{4\sqrt{5}}{5}}=\cfrac{\sqrt{5}a}{4}\),
即 \(\rho_{_{C}}=|OC|=\cfrac{\sqrt{5}a}{4}\), 由 \(|OC|=\cfrac{3\sqrt{5}}{2}=\cfrac{\sqrt{5}a}{4}\),解得 \(a=6\) .

 和直角坐标系相比较,大家对极坐标系的印象很不清晰,遂将与之相关的知识点都加以整合,便于理解和查阅。
和直角坐标系相比较,大家对极坐标系的印象很不清晰,遂将与之相关的知识点都加以整合,便于理解和查阅。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号