相关点法
比较奇怪的是，明明相关点法在高中数学中的许多章节中都有涉及，但学生就是体会不到，理解不了，许多学生对此很是陌生。
前言
通俗地理解相关点法，比如某人借助其父亲的人脉，融入到其父亲的交际圈中，就是相关点法应用的一个例子。
相关点法
用相关点法求轨迹方程的情形：
①某个动点 \(P\) 在已知方程的曲线上移动；②另一个动点 \(M\) 随 \(P\) 的变化而变化；③在变化过程中， \(P\) 和 \(M\) 满足一定的规律；注意相关点法可以使用在直角坐标系中，也可以使用在极坐标系中，当然也可以使用在参数方程中；
凡是给定了曲线方程 \(F(x,y)=0\) 后，对曲线通过平移变换和伸缩变换或者旋转变换[仅限特殊曲线]后得到新曲线，求新曲线方程的这类题目一般都可以考虑使用相关点法求解。而这又可以看成曲线的一种给出方式。
相关点法的基本步骤：
将所求动点 \(P\) 的坐标设为 \((x，y)\) ，令一个已知动点 \(Q\) 的坐标设为 \(Q(x_0，y_0)\) ，在寻找 \(P\) 和 \(Q\) 之间的关系，把 \(x_0\)，\(y_0\) 用 \(x\)，\(y\) 表示，然后代入点 \(Q\) 满足的方程中，整理得到的即为待求曲线的轨迹方程。
案例理解
分析：将曲线\(C_1\)的极坐标方程化为直角坐标方程为\(x^2+y^2-4y=12\)，即\(x^2+(y-2)^2=16\),
设圆上的动点为\(P(x'，y')\)，线段\(AP\)的中点为点\(Q(x，y)\)，
由\(Q\)为\(AP\)的中点，得到\(\begin{cases}x'=2x-6\\y'=2y\end{cases}\)，代入\(x^2+y^2-4y=12\)，
即\((2x-6)^2+(2y)^2-4(2y)=12\)，整理为\((x-3)^2+(y-1)^2=4\)；
即点\(Q\)的轨迹\(C_2\)的直角坐标方程为\((x-3)^2+(y-1)^2=4\)；
提示：在极坐标系中，使用相关点法，得到所求曲线的极坐标方程为：\(\rho=a\cos\theta\)
典例剖析
（1）求直线\(l\)被曲线\(C\)截得的弦长\(|OA|\)。
分析：可以从以下四个角度思考，
①利用两点间的距离公式；
【法1】直线\(l\)的普通方程为\(y=\sqrt{3}x\)，圆\(C\)的普通方程为\(x^2+(y-2)^2=2^2\)，
联立消掉\(y\)，得到\(x^2-\sqrt{3}x=0\)，
解得，\(\left\{\begin{array}{l}{x_1=0}\\{y_1=0}\end{array}\right.\)，或\(\left\{\begin{array}{l}{x_2=\sqrt{3}}\\{y_2=3}\end{array}\right.\)，
由两点间距离公式得到\(|OA|=2\sqrt{3}\)。
②直线和圆相交求弦长的几何方法；
【法2】直线为\(\sqrt{3}x-y=0\)，圆心为\(C(0，2)\)，
则圆心到直线的距离为\(d=\cfrac{|0-2|}{2}=1\)，又半径为\(2\)，
故半弦长为\(\sqrt{2^2-1^2}=\sqrt{3}\)，则弦长\(|OA|=2\sqrt{3}\)。
③直线的参数方程法；
【法3】由于直线的普通方程为\(y=\sqrt{3}x\)，经过点\((0，0)\)，斜率\(k=\sqrt{3}\)，倾斜角\(\theta=\cfrac{\pi}{3}\);
直线\(l\)的参数方程为\(\left\{\begin{array}{l}{x=0+\cfrac{1}{2}t}\\{y=0+\cfrac{\sqrt{3}}{2}t}\end{array}\right.(t为参数)\)，
将其代入圆的普通方程\(x^2+(y-2)^2=2^2\)，
整理得到\(t^2-2\sqrt{3}t=0\)，
解得\(t_1=0\)，\(t_2=2\sqrt{3}\)，
则弦长\(|OA|=|t_1-t_2|=2\sqrt{3}\)。
解后反思：直线\(l\)的参数方程还可以为\(\left\{\begin{array}{l}{x=1+\cfrac{1}{2}t}\\{y=\sqrt{3}+\cfrac{\sqrt{3}}{2}t}\end{array}\right.(t为参数)\)，得到\(t^2+(4-2\sqrt{3})t+4-4\sqrt{3}=0\)，
同理可得，\(|OA|=|t_1-t_2|=2\sqrt{3}\);
④极坐标法；
【法4】直线的极坐标方程为\(\theta=\cfrac{\pi}{3}\)，圆的极坐标方程为\(\rho=4sin\theta\)，
二者联立，得到\(\rho=4sin\cfrac{\pi}{3}=2\sqrt{3}\)。即所求弦长\(|OA|=2\sqrt{3}\)。
解后反思：本题目中直线\(l\)的极坐标方程可以是\(\rho sin(\theta-\cfrac{\pi}{3})=0\)，也可以是\(\theta=\cfrac{\pi}{3}\)，说明同样的直线\(l\)的极坐标方程可能不唯一；
（2）从极点做曲线\(C\)的弦，求弦的中点\(M\)轨迹的极坐标方程。
分析：可以从以下三个角度思考：
①利用平面直角坐标系下的中点公式；
【法1】在平面直角坐标系中，设过坐标原点的直线和圆相交于点\(P(x_0，y_0)\)，则所得弦的中点坐标为\(M(x，y)\)
则\(\left\{\begin{array}{l}{2x=x_0}\\{2y=y_0}\end{array}\right.\)，又点\(P(x_0，y_0)\)在圆\(x^2+(y-2)^2=2^2\)上，
代入整理得到普通方程为\(x^2+(y-1)^2=1\)，
即其极坐标方程为\(\rho=2sin\theta\)，其中\(\theta\in(0，\pi)\)，而不是\(\theta\in[0，\pi)\)，以保证弦的存在。
②利用圆的参数方程；
由于圆上任意一动点\(P\)的坐标\(P(2cos\theta，2+2sin\theta)\)，则弦的中点\(M(cos\theta，1+sin\theta)\)，
即点\(M\)的参数方程为\(\left\{\begin{array}{l}{x=cos\theta}\\{y=1+sin\theta}\end{array}\right.(\theta为参数)\)，
消去参数\(\theta\)，得到普通方程为\(x^2+(y-1)^2=1\)，
即其极坐标方程为\(\rho=2sin\theta\)，其中\(\theta\in(0，\pi)\)，而不是\(\theta\in[0，\pi)\)，以保证弦的存在。
③利用极坐标法；
【法3】曲线\(C\)的极坐标方程为\(\rho=4sin\theta\)，过极点的直线的极坐标方程为\(\theta=\alpha\)，
设直线和曲线\(C\)的交点的极坐标为\((\rho_1，\alpha)\)，则弦的中点\(M\)的极坐标为\((\rho，\alpha)\)，
由题目可知，\(\rho_1=2\rho\)，代入曲线\(C\)的极坐标方程为\(2\rho=4sin\alpha\)，
得到\(\rho=2sin\alpha\)，其中\(\alpha\in(0，\pi)\)。
故弦的中点\(M\)轨迹的极坐标方程为\(\rho=2sin\alpha\)，其中\(\alpha\in(0，\pi)\)。
说明：由于弦的中点要存在，则必须保证\(\rho\neq 0\)，即原来的\(\alpha\in[0，\pi)\)必须变为\(\alpha\in(0，\pi)\)。
对应练习
提示：设点\(P(x，y)\)，点\(Q(x_1，y_1)\)， 点\(F_1(-\sqrt{6}，0)\)，
由\(\overrightarrow{OP}=\cfrac{1}{2}(\overrightarrow{OF_1}+\overrightarrow{OQ})\)，则可知点\(P\)为线段\(F_1Q\)的中点，
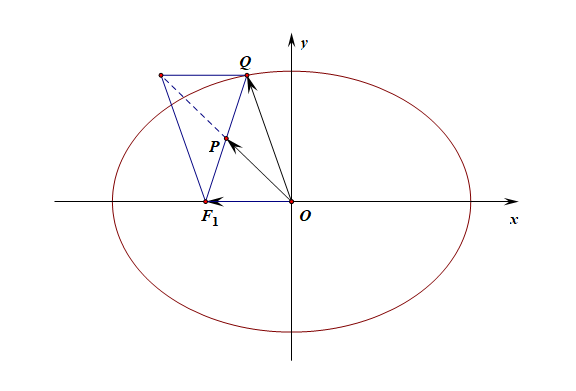
得到\(\left\{\begin{array}{l}{2x=-\sqrt{6}+x_1}\\{2y=y_1,}\end{array}\right.\quad\)，变形得到\(\left\{\begin{array}{l}{x_1=2x+\sqrt{6}}\\{y_1=2y,}\end{array}\right.\)
将其代入\(\cfrac{x^2}{16}+\cfrac{y^2}{10}=1\)，得到\(\cfrac{(2x+\sqrt{6})^2}{16}+\cfrac{2y^2}{5}=1\).
即点\(P\)的轨迹方程为\(\cfrac{(2x+\sqrt{6})^2}{16}+\cfrac{2y^2}{5}=1\)。
分析：由双曲线的方程可得\(a=3\)，\(b=1\)，\(c=\sqrt{10}\)，则\(F_{1}(-\sqrt{10}, 0)\)，\(F_{2}(\sqrt{10}, 0)\)
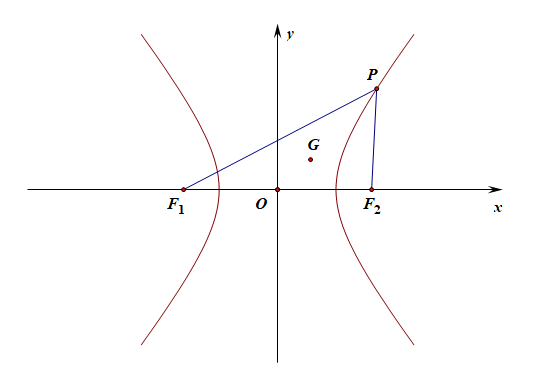
设点\(P(m, n)\)，则\(\cfrac{m^{2}}{9}-n^{2}=1\)，设\(\triangle PF_1F_2\)的重心\(G(x, y)\)
则由三角形的重心坐标公式可得\(x=\cfrac{m+\sqrt{10}-\sqrt{10}}{3}\)，\(y=\cfrac{n+0+0}{3}\)
可得\(m=3x\)，\(n=3y\)，代入双曲线\(\cfrac{x^2}{9}-y^2=1\)方程，
化简可得\(x^{2}-9 y^{2}=1\)，故\(\triangle PF_{1}F_{2}\)的重心\(G\)的轨迹方程是\(x^{2}-9 y^{2}=1\quad(y\neq 0)\) [1]
备注：三角形\(\triangle ABC\)的重心\(M\)的坐标公式：若三角形的三个顶点坐标分别为\(A(x_1，y_1)\)，\(B(x_2，y_2)\)，\(C(x_3，y_3)\)，则其重心\(M(x，y)\)满足\(x=\cfrac{x_1+x_2+x_3}{3}\)，\(y=\cfrac{y_1+y_2+y_3}{3}\)。相关重心坐标公式
相关应用
法1：相关点法，设函数\(y=\ln x\)图像上的任意一点坐标\(P(x',y')\)，其关于直线\(x=1\)的对称点的坐标为\(Q(x,y)\)，
则有\(\left\{\begin{array}{l}{\cfrac{x+x'}{2}=1}\\{y=y'}\end{array}\right.\quad\) 即\(\left\{\begin{array}{l}{x'=2-x}\\{y'=y}\end{array}\right.\)
由于点\(P(x',y')\)在函数\(y=\ln x\)图像上，将其代入，得到\(y=ln(2-x)\)，故选\(B\).
法2：利用特殊点法，函数\(y=\ln x\)过定点\((1,0)\)，而点\((1,0)\)关于直线\(x=1\)对称的点还是点\((1,0)\)，只有\(y=\ln (2-x)\)过此点，故选项\(B\)正确.
法3：利用图像变换法，由于\(y=lnx\)关于\(y\)轴对称的函数为\(y=ln(-x)\)，将\(y=ln(-x)\)向右平移两个单位得到\(y=ln[-(x-2)]=ln(2-x)\)，即得到所求函数，故选\(B\).
解后反思：法1为这类题目的通用方法，尤其是对称直线变为\(2x-y+3=0\)型的直线时，更能显示相关点法的强大作用。
从形上刻画：向左平移\(\cfrac{\pi}{4}\)个单位得到；
从数上刻画：用\(x+\cfrac{\pi}{4}\Rightarrow x\)，
原因分析：相位变换即左右平移的本质是用\(x+\phi\)替换\(x\)后整理得到的；
故由\(2(x+\phi)-\cfrac{\pi}{3}=2x+2\phi-\cfrac{\pi}{3}=2x+\cfrac{\pi}{6}\)，
解得\(\phi=\cfrac{\pi}{4}\)，[左加右减的口诀是用在\(x+\phi=x+\cfrac{\pi}{4}\)上]
即用\(x+\cfrac{\pi}{4}\)替换\(x\)，故向左平移\(\cfrac{\pi}{4}\)个单位得到；[2]
从形上刻画：横坐标缩短为原来的\(\cfrac{1}{3}\)倍得到；
从数上刻画：用\(3x\Rightarrow x\)，
原因分析：周期变换即横向伸缩的本质是用\(\omega x\)替换\(x\)后整理得到的；
\(y=sin(2x-\cfrac{\pi}{3})\)的原有横坐标系数\(\omega_0=2\)，
显然\(y=sin(6x-\cfrac{\pi}{3})\)是表达式\(y=sin(2x-\cfrac{\pi}{3})\)中的\(x\)被\(3x\)替换后得到的，[3]
\(y=sin[2\times (3x)-\cfrac{\pi}{3}]=sin(6x-\cfrac{\pi}{3})\)，
分析：把函数\(y=3^x\)的图像沿\(x\)轴向左平移\(m(m>0)\)个单位长度，
得到\(y=3^{x+m}=3^x\times 3^m=f(x)\)，又题目已知\(f(x)=10\times 3^x\)
故\(3^m=10\)，则\(f(m)=10\times 3^m=10\times 10=100\)，故选\(D\)。
(1).求曲线 \(C_{1}\)， \(C_{2}\) 的极坐标方程;
解析 : 曲线 \(C_{1}: x^{2}+(y-3)^{2}=9\)， 即 \(x^{2}+y^{2}-6y=0\)，所以曲线 \(C_{1}\) 的极坐标方程为 \(\rho=6\sin\theta\).
设 \(B(\rho, \theta)\)， 则 \(A(\rho, \theta-\cfrac{\pi}{2})\)，[此处使用了相关点法]
由于点\(A\)在曲线\(C_1\)上，故满足曲线\(C_1\)的方程，则有 \(\rho=6\sin(\theta-\cfrac{\pi}{2})=-6\cos\theta\).
所以曲线 \(C_{2}\) 的极坐标方程为 \(\rho=-6\cos\theta\).
(2). 射线 \(\theta=\cfrac{5\pi}{6}(\rho>0)\) 与曲线 \(C_{1}\)， \(C_{2}\) 分别交于 \(P\)， \(Q\) 两点, 定点 \(M(-4,0)\)，求 \(\triangle MPQ\) 的面积.
解析： \(M\) 到射线 \(\theta=\cfrac{5\pi}{6}(\rho>0)\) 的距离为 \(d=4\sin\cfrac{5\pi}{6}=2\)，
射线 \(\theta=\cfrac{5\pi}{6}(\rho>0)\) 与曲线 \(C_{1}\) 的交点 \(P(\rho_{_{P}}, \cfrac{5\pi}{6})\)， 其中，\(\rho_{_{P}}=6\sin\cfrac{5\pi}{6}=3\)，
射线 \(\theta=\cfrac{5\pi}{6}(\rho>0)\) 与曲线 \(C_{2}\) 的交点 \(Q(\rho_{_{Q}}, \cfrac{5\pi}{6})\)， 其中， \(\rho_{_{Q}}=-6\cos\cfrac{5\pi}{6}=3\sqrt{3}\)
则 \(|PQ|=|\rho_{_{P}}-\rho_{_{Q}}|=3\sqrt{3}-3\)， 则 \(S_{\triangle MPQ}=\cfrac{1}{2}\cdot|PQ|\cdot d=3\sqrt{3}-3\).
限制\(y\neq 0\)，是为了保证三角形存在。 ↩︎
用相关点法作深度分析，设变换前函数图像上的任一点坐标为\(P(x,y)\)，
变换后函数图像上对应的点的坐标为\(P'(x_1,y_1)\)；
则其施行的变换公式为\(\left\{\begin{array}{l}{x_1=x+\phi}\\{y_1=y}\end{array}\right.\)，即其逆变换公式为\(\left\{\begin{array}{l}{x=x_1-\phi}\\{y=y_1}\end{array}\right.\)，
将其代入已知的函数解析式，得到\(y_1=\sin[2(x_1-\phi)-\cfrac{\pi}{3}]\)，整理为\(y_1=\sin(2x_1-2\phi-\cfrac{\pi}{3})\)，
变换解释后我们往往就会将下标去掉，得到\(y=\sin(2x-2\phi-\cfrac{\pi}{3})\)，其应该等价于\(y=\sin(2x+\cfrac{\pi}{6})\)，
于是解得\(\phi=-\cfrac{\pi}{4}\)，故我们是用\(x_1-(-\cfrac{\pi}{4})=x_1+\cfrac{\pi}{4}\)替换的原解析式中的\(x\)，
由于是\(+\)，故应该向左平移\(\cfrac{\pi}{4}\)个单位； ↩︎用相关点法作深度分析，设变换前函数图像上的任一点坐标为\(P(x,y)\)，
变换后函数图像上对应的点的坐标为\(P'(x_1,y_1)\)；
则其施行的变换公式为\(\left\{\begin{array}{l}{x_1=\cfrac{1}{3}x}\\{y_1=y}\end{array}\right.\)，即其逆变换公式为\(\left\{\begin{array}{l}{x=3x_1}\\{y=y_1}\end{array}\right.\)，
将其代入已知的函数解析式，得到\(y_1=\sin[2(3x_1)-\cfrac{\pi}{3}]\)，整理为\(y_1=\sin(6x_1-\cfrac{\pi}{3})\)，
变换解释后我们往往就会将下标去掉，得到\(y=\sin(6x-\cfrac{\pi}{3})\)；
故我们是用\(3x_1\)替换的原解析式中的单独的\(x\)，注意不是替换\(2x\)这个整体， ↩︎
浙公网安备 33010602011771号