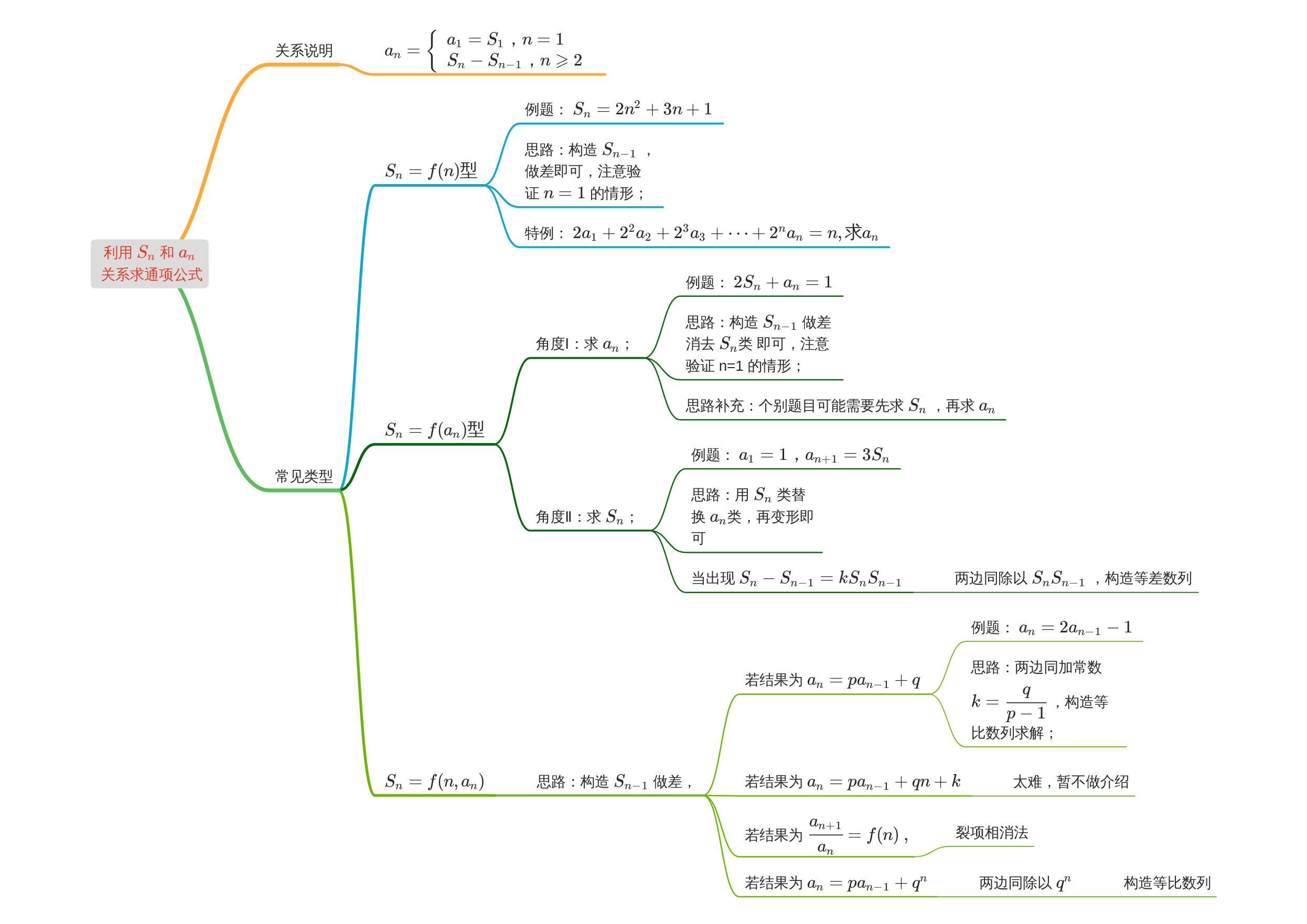
利用 $a_n$ 与 $S_n$ 的关系求通项 $a_n$
前言
由\(a_n\)与\(S_n\)的关系求数列\(\{a_n\}\)的通项公式,在求通项公式题型中占有比较大的份额,是一个重要的求解思路和方法。是要求重点掌握的类型。
方法依据
- 由\(a_n\)与\(S_n\)的关系求数列\(\{a_n\}\)的通项公式【要求重点掌握的类型】
方法:熟练记忆\(a_n\)与\(S_n\)的关系\(a_n=\begin{cases}S_1 &n=1\\S_n-S_{n-1} &n\ge 2\end{cases}\),并灵活运用注意:①这是个分段函数,故求其解析式应该分段求解,容易忘记求解\(n=1\)的情形②必须验证能否合二为一,如果能就写成一个式子,如果不能,写成分段数列的形式。③若题目中是\(a_{n+1}\),则\(a_{n+1}\)\(=\)\(S_{n+1}\)\(-\)\(S_n\),而不是\(a_{n+1}\)\(=\)\(S_{n}\)\(-\)\(S_{n-1}\),切记!。
如何识别
大家都知道,数列中的\(S_n\),\(a_n\),\(n\)都是变量,为便于表述,我们做以下的约定:(只关注变量,暂时不关注常数和数字系数)
当题目中只包含\(S_n\)和\(n\)时,比如\(2S_n=n^2+n+1\),或\(S_n-n^2-2n-1=0\)等,称为\(S_n=f(n)\);
当题目中只包含\(S_n\)和\(a_n\)时,比如\(2S_n=a_n^2+1\),或\(S_n-a_n^2-a_n-1=0\)等,称为\(S_n=f(a_n)\);
当题目中只包含\(S_n\)和\(a_n,n\)时,比如\(2S_n=a_n^2+n+1\),或\(S_n-a_n^2-n+3=0\)等,称为\(S_n=f(a_n,n)\);
当题目中包含\(a_n\),\(a_{n+1}\),\(a_{n-1}\),\(\cdots\)等,我们称为\(a_n\)类;
当题目中包含\(S_n\),\(S_{n+1}\),\(S_{n-1}\),\(\cdots\)等,我们称为\(S_n\)类;
构建模型
- 角度1:若已知形如\(S_n=f(n)\)
思路:仿照已知条件,构造\(S_{n-1}\),用两者作差消去\(S_n\)类即可解;
分析:当\(n=1\)时,\(S_1=a_1=6\),
当\(n\ge 2\)时,由已知可得\(S_{n-1}=2(n-1)^2+3(n-1)+1\),
又\(S_n=2n^2+3n+1\),两式相减得到
\(n\ge 2\)时,\(a_n=S_n-S_{n-1}=4n+1\),
由于\(n=1\)时,\(a_1=6\),不满足上式,故需要将通项公式写成分段函数形式,
即所求通项公式为\(a_n=\begin{cases}6,&n=1\\4n+1,&n\ge 2\end{cases}\)。
分析:由已知可得,当\(n\ge 2\)时,\(2^1a_1+2^2a_2+2^3a_3+\dots+2^{n-1}a_{n-1} = n-1\),
两式作差得到
当\(n\ge 2\)时,\(2^na_n =1\),即\(a_n=\cfrac{1}{2^n}=(\cfrac{1}{2})^n\),
又当\(n=1\)时,\(2^1a_1=1\),即\(a_1=\cfrac{1}{2}\),满足上式,
故所求通项公式为\(a_n=(\cfrac{1}{2})^n,n\in N^*\)。
分析:积式用商
当\(n \ge 1\)时,\(b_1\cdot b_2 \cdot b_3 \cdots b_n= 2^{S_n} ①\),
当\(n \ge 2\)时,\(b_1\cdot b_2 \cdot b_3 \cdots b_{n-1}= 2^{S_{n-1}}②\),两式相除得到
当\(n \ge 2\)时,\(b_n=2^{S_n-S_{n-1}}=2^{a_n}\),即\(b_n=2^{a_n}=2^n\),
再验证,当\(n=1\)时,由已知式子可知\(b_1=2^{S_1}=2^{a_1}=2\),满足上式,故数列\(\{b_n\}\)的通项公式为\(b_n=2^n\).
- 角度2:已知形如\(S_n=f(a_n)\),有两个求解方向:
①若求\(a_n\) ,思路:设法消去\(S_n\),即构造\(S_{n-1}\),作差即可求解;
分析:由已知\(2S_n+a_n=1\)可得,
当\(n\ge 2\)时,\(2S_{n-1}+a_{n-1}=1\),两式相减得到
当\(n\ge 2\)时,\(3a_n-a_{n-1}=0\),
又\(n=1\)时,\(2S_1+a_1=1\),解得\(a_1=\cfrac{1}{3}\),
故可知\(\cfrac{a_n}{a_{n-1}}=\cfrac{1}{3}\),
即数列\(\{a_n\}\)是首项为\(\cfrac{1}{3}\),公比为\(\cfrac{1}{3}\)的等比数列,
通项公式为\(a_n=\cfrac{1}{3^n}(n\in N^*)\)。
②若求\(S_n\) ,思路:消去\(a_n\),用\(s_n-s_{n-1}=a_n\)代换\(a_n\)即可求解。
分析:由\(a_{n+1}=S_{n+1}-S_n\),代入已知式子得到,
\(S_{n+1}-S_n=3S_n\),整理得到,\(S_{n+1}=4S_n\),
由\(S_1=a_1=1\neq 0\),故数列\(\{S_n\}\)是首项是1,公比为4的等比数列,
故\(S_n=1\cdot 4^{n-1}=4^{n-1}(n\in N^*)\)。
解后反思:【理科学生用】若用以上的两个思路都不能奏效,则可以考虑先计算出数列的前几项,归纳猜想一个结论,然后用数学归纳法进行证明。
- 角度3:已知形如\(S_n=f(n,a_n)\)
思路:构造\(S_{n-1}\),两者作差后,
①若出现\(a_{n+1} =pa_n + q(p,q\in R,p\neq 1,q\neq 0)\) ,两边同加常数\(k=\cfrac{q}{p-1}\)构造等比数列。 [1]
分析:由已知当\(n\ge 2\)时,\(S_{n-1}=2a_{n-1}+(n-1)\),两式相减得到
\(n\ge 2\)时,\(a_n=2a_n-2a_{n-1}+1\),整理得到\(a_n=2a_{n-1}-1\),两边同加-1,
即\(a_n-1=2(a_{n-1}-1)\),故\(a_1-1=1\neq 0\),
故数列\(\{a_n-1\}\)是首项为1,公比为2的等比数列,
故\(a_n-1=1\cdot 2^{n-1}\),故\(a_n=2^{n-1}+1(n\in N^*)\)。
②若出现\(a_{n+1} =pa_n+qn+k\),两边同加关于\(n\)的一次式构造等比数列。(较难的类型)
分析:设\(a_{n+1}+p(n+1)+q=2(a_n+pn+q)\),打开整理得到,\(p=3\),\(q=4\),
整理都得到\(a_{n+1}+3(n+1)+4=2(a_n+3n+4)\),
由首项\(a_1+3\cdot 1+4=8\neq 0\) ,故数列\(\{a_n+3n+4\}\)是首项为 \(8\),公比为 \(2\) 的等比数列,
故\(a_n+3n+4=8\cdot 2^{n-1}\),故\(a_n=2^{n+2}-3n-4(n\in N^*)\)。
分析:当\(n=1\)时,\(\cfrac{1}{a_1a_2}=\cfrac{1}{2\times3}=\cfrac{1}{6}\)①;
当\(n=2\)时,\(\cfrac{1}{a_1a_2}+\cfrac{1}{a_2a_3}=\cfrac{2}{2\times4}=\cfrac{1}{4}\)②;
①-②得到\(\cfrac{1}{a_2a_3}=\cfrac{1}{12}\)
则有\(a_1\cdot (a_1+d)=6\)③;\((a_1+d)(a_1+2d)=12\)④,
由③④解得\(a_1=2\),\(d=1\);故\(a_n=n+1\);
思维导图
典例剖析
法1:常规方法,先求得\(n\ge 2\)时,\(a_{n+1}=3a_n+2\),
再变形为\(a_{n+1}+1=3(a_n+1)\),
再验证,当\(n=1\)时,\(a_2=8\),\(a_2+1=9=3(a_1+1)\),满足上式;
故数列\(\{a_n+1\}\)是首项为\(3\),公比为\(3\)的等比数列,
故\(a_n+1=3\cdot3^{n-1}=3^n\),所以\(a_n=3^n-1\),
从而求得\(S_n=\cfrac{3^{n+1}}{2}-n-\cfrac{3}{2}\).
法2:将\(a_{n+1}=S_{n+1}-S_n\)代入\(a_{n+1}=2S_n+2n+2\),整理得到\(S_{n+1}=3S_n+2n+2\),
再变形为\(S_{n+1}+p(n+1)+q=3(S_n+pn+q)(p、q为常数)\),可解得\(p=1,q=\cfrac{3}{2}\),
即\(S_{n+1}+(n+1)+\cfrac{3}{2}=3(S_n+n+\cfrac{3}{2})\),
则数列\(\{S_n+n+\cfrac{3}{2}\}\)是首项为\(a_1+1+\cfrac{3}{2}=\cfrac{9}{2}\),公比为3的等比数列;
故\(S_n+n+\cfrac{3}{2}=\cfrac{9}{2}\cdot 3^{n-1}\),整理得到\(S_n=\cfrac{3^{n+1}}{2}-n-\cfrac{3}{2}\).
(1)求数列\(\{a_n\}\)的通项公式。
分析:本题是利用\(a_n\)和\(S_n\)的关系解题,或者是利用“退一法”解题。
由题目可知,\(n\ge 1\),\(a_1+3a_2+\cdots+(2n-1)a_n=2n①\)得到,
当\(n\ge 2\),\(a_1+3a_2+\cdots+(2n-3)a_{n-1}=2(n-1)②\)
两式相减得到
\(n\ge 2,(2n-1)a_n=2\),
从而得到\(a_n=\cfrac{2}{2n-1}(n\ge 2)\),
接下来验证\(n=1\)是否满足
当\(n=1\)时,\(a_1=2=\cfrac{2}{2\times 1-1}\),满足上式,
故数列\(\{a_n\}\)的通项公式为\(a_n=\cfrac{2}{2n-1}(n\in N^*)\).
(2)求数列\(\{\cfrac{a_n}{2n+1}\}\)的前\(n\)项和\(S_n\)。
分析:结合第一问,数列\(\cfrac{a_n}{2n+1}=\cfrac{2}{(2n-1)(2n+1)}=\cfrac{1}{2n-1}-\cfrac{1}{2n+1}\)
故数列的前\(n\)项和\(S_n=(\cfrac{1}{2\times1-1}-\cfrac{1}{2\times 1+1})+(\cfrac{1}{2\times 2 -1}-\cfrac{1}{2\times 2+1})+\cdots+(\cfrac{1}{2n-1}-\cfrac{1}{2n+1})\)
\(=1-\cfrac{1}{2n+1}=\cfrac{2n}{2n+1}\)。
分析:当\(n\ge 1\)时,\(S_n=2a_n-2^{n+1}\)
当\(n\ge 2\)时,\(S_{n-1}=2a_{n-1}-2^n\)
两式相减得到,当\(n\ge 2\)时,\(a_n=2a_n-2a_{n-1}-(2^{n+1}-2^n)\)
整理得到,\(a_n=2a_{n-1}+2^n(n\ge 2)\), 两边同除以\(2^n\),得到
\(\cfrac{a_n}{2^n}=\cfrac{a_{n-1}}{2^{n-1}}+1(n\ge 2)\),
令\(n=1\),\(a_1=2a_1-2^2\),得到\(a_1=4\),则\(\cfrac{a_1}{2^1}=2\);
故数列\(\{\cfrac{a_n}{2^n}\}\)是以\(\cfrac{a_1}{2^1}=2\)为首项,以1为公差的等差数列,
故\(\cfrac{a_n}{2^n}=2+(n-1)\cdot1\),即数列的\(\{a_n\}\)的通项公式为\(a_n=(n+1)2^n\)。
分析:当\(n=1\)时,\(a_1^2+2a_1=4a_1+3\),求得\(a_1=3\)或\(a_1=-1\)(舍去),
当\(n\ge 2\)时,\(a_{n-1}^2+2a_{n-1}=4S_{n-1}+3\),两式相减,
即\(n\ge 2\)时,\(a_n^2-a_{n-1}^2+2a_n-2a_{n-1}=4a_n\),
即\(n\ge 2\)时,\(a_n^2-a_{n-1}^2-2(a_n+a_{n-1})=0\),
即\(n\ge 2\)时,即\((a_n-a_{n-1})(a_n+a_{n-1})-2(a_n+a_{n-1})=0\),
由于\(a_n+a_{n-1}>0\),故得到\(a_n-a_{n-2}=2(n\ge 2)\),
故数列\(\{a_n\}\)是首项为\(3\),公差为\(2\)的等差数列,
则所求通讯公式为\(a_n=3+(n-1)\times 2=2n+1(n\in N^*)\)。
分析:由\(\sqrt{a_1}+\sqrt{a_2}+\sqrt{a_3}+\cdots+\sqrt{a_n}=n^2\),
故当\(n\ge 2\)时,\(\sqrt{a_1}+\sqrt{a_2}+\sqrt{a_3}+\cdots+\sqrt{a_{n-1}}=(n-1)^2\),
两式相减,得到
当\(n\ge 2\)时,\(\sqrt{a_n}=n^2-(n-1)^2=2n-1\),即\(a_n=(2n-1)^2\),
验证\(n=1\)时,也满足上式。故通项公式为\(a_n=(2n-1)^2,n\in N^*\),
\(a_{n+1}=(2n+1)^2=4n^2+4n+1\),
则\(\cfrac{1}{a_{n+1}-1}=\cfrac{1}{4n(n+1)}=\cfrac{1}{4}(\cfrac{1}{n}-\cfrac{1}{n+1})\)
故\(T_n=\cfrac{1}{4}[(1-\cfrac{1}{2})+(\cfrac{1}{2}-\cfrac{1}{3})+\cdots+(\cfrac{1}{n}-\cfrac{1}{n+1})]\)
\(=\cfrac{1}{4}\cdot \cfrac{n}{n+1}=\cfrac{n}{4n+4}\)
高阶例题
当你能判断题目是属于\(a_n\)和\(S_n\)的关系的题目,但是用上述思路也不能求解\(a_n\)时,说明不是能直接求解\(a_n\)的类项,此时可能还需要先求解\(S_n\),再由\(S_n\)转而求解\(a_n\)。[即被动求\(S_n\),再求\(a_n\)]
分析:本题目尝试直接求解\(a_n\)而不得,故考虑需要先求解\(S_n\);
由于\(S_n\)是\(a_n\)与\(\cfrac{1}{a_n}\)的等差中项,
则有\(2S_n=a_n+\cfrac{1}{a_n}\),
当\(n=1\)时,上式变为\(2a_1=a_1+\cfrac{1}{a_1}\),解得\(a_1^2=1\),
由于\(a_n>0\),则得到\(a_1=1\),
当\(n\geqslant 2\)时,上式变化为\(2S_n\cdot a_n=a_n^2+1\),
即\(2S_n(S_n-S_{n-1})=(S_n-S_{n-1})^2+1\),整理为\(S_n^2-S_{n-1}^2=1\),
故\(\{S_n^2\}\)是首项为\(S_1^2=a_1^2=1\),公差为\(1\)的等差数列,则\(S_n^2=1+(n-1)\times 1=n\),
则\(S_n=\sqrt{n}(n\in N^*)\),
由上可知,当\(n\geqslant 2\)时,\(S_{n-1}=\sqrt{n-1}\),
两式相减,得到\(S_n-S_{n-1}=a_n=\sqrt{n}-\sqrt{n-1}(n\geqslant 2)\)
再验证,\(n=1\)时,\(a_1=1=\sqrt{1}-\sqrt{1-1}\),故满足上式,
综上所述,\(a_n=\sqrt{n}-\sqrt{n-1}(n\in N^*)\)。
解析:由于 \(a_n>0\),故 \(S_n>0\) 且 \(S_{n-1}>0\) ,又由于\(a_n=S_n-S_{n-1}\) ,
则 \(a_n=(\sqrt{S_n})^2-(\sqrt{S_{n-1}})^2=(\sqrt{S_n}+\sqrt{S_{n-1}})(\sqrt{S_n}-\sqrt{S_{n-1}})\)
由题目可知,\(a_n=\sqrt{S_n}-\sqrt{S_{n-1}}\),则有\((\sqrt{S_n}+\sqrt{S_{n-1}})(\sqrt{S_n}-\sqrt{S_{n-1}})=\sqrt{S_n}+\sqrt{S_{n-1}}\)
由于 \(\sqrt{S_n}+\sqrt{S_{n-1}}>0\) ,约分得到 \(\sqrt{S_n}-\sqrt{S_{n-1}}=1\),
则数列 \(\{\sqrt{S_n}\}\) 是首项为 \(\sqrt{S_1}=\sqrt{a_1}=1\) ,公差为 \(1\) 的等差数列,
则 \(\sqrt{S_n}=1+(n-1)\cdot 1=n\) ,故 \(S_n=n^2\),
当 \(n\geqslant2\) 时,\(a_n=S_n-S_{n-1}=n^2-(n-1)^2=2n-1\),
又由于 \(a_1=1\) 满足上式,故 \(a_n=2n-1\),\(n\in N^*\) ,
则 \(\cfrac{1}{a_{n}\cdot a_{n+1}}=\cfrac{1}{(2n-1)(2n+1)}=\cfrac{1}{2}(\cfrac{1}{2n-1}-\cfrac{1}{2n+1})\)
令所求数列的前 \(n\) 项和 \(T_{n}\) ,
则 \(T_{15}=\cfrac{1}{2}[(1-\cfrac{1}{3})+(\cfrac{1}{3}-\cfrac{1}{5})+\cdots+(\cfrac{1}{29}-\cfrac{1}{31})]\)
\(=\cfrac{1}{2}(1-\cfrac{1}{31})=\cfrac{15}{31}\).
对应练习
提示:本题目属于\(S_n=f(a_n)\)且直接求解\(a_n\)的形式;
当\(n\geqslant 2\)时,\(S_{n-1}=\cfrac{2}{3}a_{n-1}+\cfrac{1}{3}\),
两式作差得到,当\(n\geqslant 2\)时, \(a_n=S_n-S_{n-1}=\cfrac{2}{3}a_n-\cfrac{2}{3}a_{n-1}\),
变形整理为\(a_n=-2a_{n-1}(n\geqslant 2)\),
当\(n=1\)时,\(a_1=S_1=\cfrac{2}{3}a_1+\cfrac{1}{3}\),解得\(a_1=1\neq 0\),
故\(\cfrac{a_n}{a_{n-1}}=-2(n\geqslant 2)\),
即数列\(\{a_n\}\)是首项为\(1\),公比为\(-2\)的等比数列,故\(a_n=a_1\cdot q^{n-1}=(-2)^{n-1}(n\in N^*)\).
提示:本题目属于\(S_n=f(n,a_n)\)且直接求解\(a_n\)的形式;
当\(n\geqslant 2\)时,\(S_{n-1}=2a_{n-1}-(n-1)\),
两式做差,得到\(a_n=S_n-S_{n-1}=(2a_n-n)-[2a_{n-1}-(n-1)](n\geqslant 2)\),
整理为\(a_n=2a_{n-1}+1(n\geqslant 2)\),两边同加常数\(1\),
整理为\(a_n+1=2(a_{n-1}+1)(n\geqslant 2)\),
当\(n=1\)时,原已知式子\(s_1=a_1=2a_1-1\),解得\(a_1=1\),
又由于\(a_1+1=2\neq 0\),故数列\(\{a_n+1\}\)是首项为\(a_1+1=2\),公比为\(2\)的等比数列,
故\(a_n+1=2\cdot 2^{n-1}=2^n(n\in n^*)\)
提示:本题目属于\(S_n=f(n,a_n)\)且直接求解\(a_n\)的形式;
当\(n\geqslant 2\)时,\(3S_{n-1}=(n+1)a_{n-1}\),
两式作差得到,\(3(S_n-S_{n-1})=3a_n=(n+2)a_n-(n+1)a_{n-1}(n\geqslant 2)\),
整理为\((n-1)a_n=(n+1)a_{n-1}(n\geqslant 2)\),即
由上式衍生出以下式子:
以上\(n-1\)个式子累乘得到,当\(n\geqslant 2\)时,
约分后整理为
即\(a_n=\cfrac{(n+1)n}{2}(n\geqslant 2)\),
当\(n=1\)时,\(a_1=1=\cfrac{(1+1)\times1}{2}\),故满足上式,
即所求通项公式为\(a_n=\cfrac{n(n+1)}{2}(n\in N^*)\).
提示:同于本博文的高阶例题,\(a_n=\sqrt{n}-\sqrt{n-1}(n\in N^*)\)。
提示:由已知\(a_1+2a_2+3a_3+\cdots+na_n=n(n+1)(n+2)(n\geqslant 1)\)
则有\(a_1+2a_2+3a_3+\cdots+(n-1)a_{n-1}=(n-1)n(n+1)(n\geqslant 2)\)
两式作差,得到\(na_n=n(n+1)(n+2)-(n-1)n(n+1)=n(n+1)[(n+2)-(n-1)]=3n(n+1)(n\geqslant 2)\),
则\(na_n=3n(n+1)\),即\(a_n=3(n+1)(n\geqslant 2)\),
当\(n=1\)时,由原始已知式子可得,\(a_1=1\times (1+1)\times(1+2)=6=3(1+1)\),满足上式,
故\(a_n=3(n+1)(n\in N^*)\).
提示:由已知\(a_n=2S_{n-1}+3^n(n\ge 2)\),
可得\(a_{n+1}=2S_{n}+3^{n+1}(n\ge 1)\),
两式做差,得到\(a_{n+1}-a_n=2a_n+3^{n+1}-3^n(n\geqslant 2)\),
整理为\(a_{n+1}=3a_n+2\times 3^n\),两边同除以\(3^{n+1}\),
得到\(\cfrac{a_{n+1}}{3^{n+1}}=\cfrac{a_n}{3^n}+\cfrac{2}{3}(n\geqslant 2)\),
[特别注意,此时不能判断数列\(\{\cfrac{a_n}{3^n}\}\)为等差数列,原因是上述表达式中不包含\(\cfrac{a_2}{3^2}-\cfrac{a_1}{3^1}=\cfrac{2}{3}\),这一点需要我们从题目中自己计算,并验证是否满足]
又由于\(a_1=3\),当\(n=2\)时,\(a_2=2S_1+3^2=2a_1+3^2=6+9=15\),
则\(\cfrac{a_2}{3^2}-\cfrac{a_1}{3^1}=\cfrac{15}{3^2}-\cfrac{3}{3}=\cfrac{2}{3}\),故满足上式;
即数列\(\{\cfrac{a_n}{3^n}\}\)是首项为\(\cfrac{a_1}{3^1}=1\),公差为\(\cfrac{2}{3}\)的等差数列,
故\(\cfrac{a_n}{3^n}=1+(n-1)\times \cfrac{2}{3}\),
即\(a_n=(2n+1)\cdot 3^{n-1}(n\in N^*)\)。
提示:这又是一个被动求\(S_n\),再求\(a_n\)的例子。
当\(n\geqslant 2\)时,由\(a_n=S_n-S_{n-1}\)替换给定的\(a_n=S_n \cdot S_{n-1}(n\ge 2)\)中的\(a_n\),
得到\(S_n-S_{n-1}=S_nS_{n-1}(n\geqslant 2)\),由于\(S_n\cdot S_{n-1}\neq 0\),否则\(a_1=0\),两边同除以\(S_n\cdot S_{n-1}\),
得到\(\cfrac{S_n-S_{n-1}}{S_n\cdot S_{n-1}}=1\),即\(\cfrac{1}{S_{n-1}}-\cfrac{1}{S_{n}}=1(n\geqslant 2)\),
即\(\cfrac{1}{S_{n}}-\cfrac{1}{S_{n-1}}=-1(n\geqslant 2)\),
故数列\(\{\cfrac{1}{S_n}\}\)是首项为\(\cfrac{1}{S_1}=\cfrac{1}{a_1}=\cfrac{9}{2}\),公差为\(-1\)的等差数列;
故\(\cfrac{1}{S_n}=\cfrac{9}{2}+(n-1)\times (-1)=\cfrac{11-2n}{2}\),
即\(S_n=\cfrac{2}{11-2n}(n\in N^*)\),
[以下题目转化为,已知\(S_n\),求\(a_n\)的类型;]
当\(n\geqslant 2\)时,\(S_{n-1}=\cfrac{2}{11-2(n-1)}=\cfrac{2}{13-2n}\)
两式作差,得到\(a_n=S_n-S_{n-1}=\cfrac{2}{11-2n}-\cfrac{2}{13-2n}=2(\cfrac{1}{11-2n}-\cfrac{1}{13-2n})=\cfrac{4}{(11-2n)(13-2n)}(n\geqslant 2)\),
当\(n=1\)时,\(a_1=\cfrac{2}{9}\neq \cfrac{4}{(11-2\times 1)(13-2\times 1)}=\cfrac{4}{99}\),故不满足上式,
从而得到通项公式为\(a_n=\left\{\begin{array}{l}{\cfrac{2}{9},n=1}\\{\cfrac{4}{(11-2n)(13-2n)},n\ge 2}\end{array}\right.\)


【解释】:为什么同加常数\(k=\cfrac{q}{p-1}\)就可以构造等比数列,
假设\(a_{n+1} = pa_n + q\),可以变形为\(a_{n+1}+k=p(a_n+k)\),整理得到\(a_{n+1}=pa_n+pk-k\),
则有\(k(p-1)=q\),故\(k=\cfrac{q}{p-1}\),即只要给所给的形如\(a_{n+1} = pa_n + q\)的式子两边同时
加上常数\(\cfrac{q}{p-1}\),则可以等价变形为\(a_{n+1}+k=p(a_n+k)\),接下来就可以朝等比数列考虑了。 ↩︎

 利用 $a_n$ 与 $S_n$ 的关系求数列的通项公式 $a_n$ 。
利用 $a_n$ 与 $S_n$ 的关系求数列的通项公式 $a_n$ 。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号