分类问题（分类器方法）

一.K-近邻算法（k-NearstNeighbor,kNN）

　　使用某种距离计算方法进行分类。

　　思路：如果一个样本在特征空间中的k个最邻近样本中的大多数属于某一类别，则该样本也属于这个类别。该方法所选择的邻居都是已经正确分类的对象。

　　常用向量距离：欧式 马氏 信息熵。kNN中一般使用欧式距离计算：

　                                              　

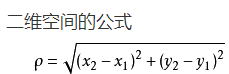
　　统计学习方法中一般要在偏差(Bias)和方差(Variance)间取得一个平衡(Tradeoff)。k的选取同理。

　　k的选取：太大：导致分类模糊，偏差过大。

                  太小：分类结果易因噪声点干扰而出现错误，此时方差较大（  受个例影响 波动较大 ，）

　　如何选取k：利用交叉验证评估一系列不同k值。

　　步骤：

　　　　（1）计算测试数据和各个训练数据之间距离

　　　　（2）按距离递增关系排序

　　　　（3）选取距离最小的k个点

　　　　（4）确定前k个点所在类别的出现频率

　　　　（5）返回前k个点中出现频率最高的类别作为测试数据的预测分类

二.朴素贝叶斯(Naive Bayes Classifier,NBC)

　　使用概率论建立分类器。

　　朴素;整个形式化过程只做最原始、最简单的假设。假设各特征之间相互独立

　　优点：所需估计参数很少、对缺失数据不敏感、算法简单、在数据较少情况下依然有效，可处理多类别问题。

　　朴素贝叶斯基本公式：

                                           

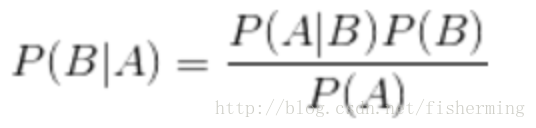
　　分类表达式：

                           

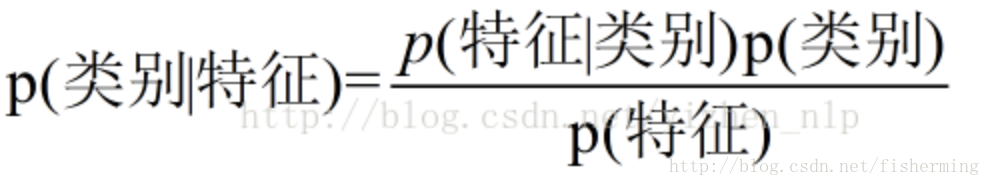
　　Note；假设各特征独立，P(ABC|T)=P(A|T) X P(B|T) X P(C|T)

三.支持向量机(Support Vetor Machine,SVM)

　　SVM通常用来进行模式识别、分类、回归分析。与其他算法相比，SVM在学习复杂的非线性方程提供更清晰、强大的方式。

　　通过寻求结构化风险最小来提高机器学习泛华能力，实现经验风险和置信范围的最小化，达到在统计量样本较小情况下，也能获得良好统计规律目的。

　　通俗来讲，是一种二分类模型，基本模型定义为：特征空间上的间隔最大的线性分类器，即SVM的学习策略便是间隔最大化，最终可转化为一个凸二次规划问题求解。

概念了解：

（1）线性可分。很容易在图中画出一条直线将这一组数据分开。数据称为线性可分数据。

　　　　　　　　　　　　　　　　　　　　

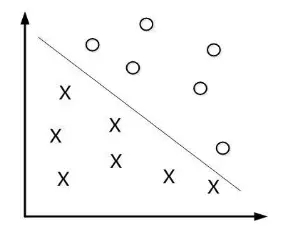
（2）分隔超平面。

　　在二维平面上，将数据集分隔开的直线称为分隔超平面。如果是三维的，分隔数据的就是一个平面。如果数据是100维的，那就需一个9维的对象对数据进行分隔，这些统称为超平面。　

　　在样本空间中，划分超平面可通过如下形式来描述：

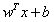　　　　        (其中w为法向量，决定超平面的方向，b为位移量，决定了超平面与原点的距离)

（3）间隔

　　如下图，有多种分隔方式，但是哪种分隔方式最好?

　　所以SVM的目标是寻找一个超平面，使得离超平面较近的异类点之间能有更大的间隔，即不必考虑所有样本点，只需让求得的超平面使得离它近的点间隔最大。

　　　　　　　　　　　　　　　　

 

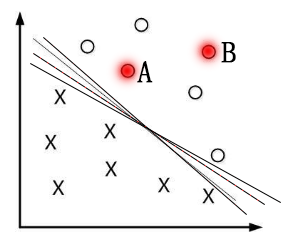
（4）支持向量。离分隔超平面最近（最小间隔）的数据点是支持向量。

 　　接下来目标：寻找最大支持向量到分隔面的距离。

                                                           

 

 　　对使用单位跃阶函数f得到 ，其中当u<0,f(u)=-1，当u>0,f(u)=+1

用一个统一公式表示间隔or数据点到分隔超平面的距离：

　　　　　　　　　　　　　　

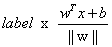
此时，如果数据处于正方向（+1类）且离分隔超平面很远的位置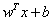，是一个很大正数，则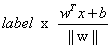会是一个很大正数；

如果数据处于负方向（-1类）且离分隔超平面很远的位置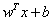，是一个很大负数，由于此时类别标签为-1，则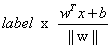,仍会是一个很大正数。

　　为找到具有最小间隔的数据点（支持向量），就要找到分类器中定义的w,b　。一旦找到支持向量，就要对该间隔最大化，可以写作:

 　　　　　　　　　　　　　　　　　　　

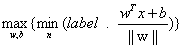
该基本型是一个凸二次规划问题，可以采用拉格朗日乘数法对其对偶问题求解求解，表达式则变为：

　　　　　　　　　　　　　　

约束条件为：

　　　　　　　　　　　　　　

 

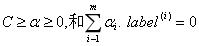
　　常数C用于控制最大化间隔和保证大部分点的函数间隔小于1。因为所有数据可能都有干扰数据，所以通过引入所谓的松弛变量，允许有些数据点可以处于分隔面错误的一侧。

根据上式可知，只要求出所有alpha,分隔超平面就可以通过这些alpha表达，这也是SVM的主要工作。　

 可参考：https://blog.csdn.net/qq_35992440/article/details/80987664

四.AdaBoost算法

　　由若干个分类器构成。

　　AdaBoost是一种迭代算法，核心思想：针对同一个训练集训练不同的分类器（弱分类器），then把这些弱分类集合起来，构成一个更强的最终分类器（强分类器）。

Adaptive Boosting（自适应），自适应在于:前一个基本分类器分错的样本会得到加强，加权后的样本再次被用来训练下一个基本分类器。同时，在每一轮中加入一个新的弱分类器，直到达到某个预定的足够小的错误率，or达到预先设定的最大迭代次数。

 　　最经常使用的弱分类器是 单层决策树（决策树桩），即层数为1的决策树。

 

　　本节使用单层决策树作为弱分类器。每一个训练数据都有一个权值系数，注意不是弱分类器系数。建立最佳单层决策树依据：每个训练数据在单层决策树中的分类结果 乘 自己权值系数  后相加的 和 最小，即分类误差最小化。

AdaBoost迭代算法步骤：

　　1.初始化训练数据的权值分布。若有N个样本，则每一个样本最开始时都赋予相同的权重：1/N

　　2.训练弱分类器。具体训练过程中：if某个样本点已被准确分类，那么在构造下一个训练集时，它的权重就被降低；相反，若某个样本点未被准确分类，那它的权重得到提高。then,权重更新的样本集被用于训练下一个分类器，整个训练过程迭代进行下去。

　　3.将各个训练得到的弱分类器组合成强分类器。加大分类误差率小的弱分类器权重。

运行过程：

　　训练数据中的每个样本，并赋予一开始相等权重，这些权重构成了向量D。

　　首先在训练数据上训练一个弱分类器并计算分类器的错误率，then在同一数据集上再次训练弱分类器。

　　在第二次训练分类器中，会重新调整每个样本权重，其中第一次分类错误的权重会提高，而第一次分类样本正确的权重会降低。AdaBoost根据每个弱分类器错误率进行计算，为每个分类器都配了一个权重α。最终所有α求和。

 

错误率定义：

                   ε=未正确分类的样本数目/所有样本数目

α计算公式：

　　　　　

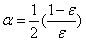
计算出α后，对权重向量D进行更新，D的计算方法如下：

　　如果某个样本被错误分类，那么该样本权重更改为：

　　　　　　　　

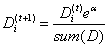
　　如果某个样本被正确分类，那么该样本权重更改为：

　　　　　　　　

 计算出D后，AdaBoost开始下一轮迭代。不断重复训练和调整权重，直到训练错误率为0，或者弱分类器的数目达到用户的指定值。

五.决策树(Decision Tree)

1.决策树的基本概念

　　决策树是一个非参数的监督式学习方法，又称为判定树，是运用于分类的一种树结构。

2.决策树的学习过程

3.信息熵

4.Scikit-learn决策树算法库类介绍

 

六.Multi-layer Perceptron 多层感知器