[AcWing 4486] 数字操作

数论 + 贪心

---

点击查看代码

#include<bits/stdc++.h>

using namespace std;

typedef long long LL;

const int N = 1e6 + 10;


int n;

void solve()
{
    cin >> n;
    int res = 1, m = 0;
    vector<int> a;
    for (int i = 2; i <= n / i; i ++) {
        if (n % i == 0) {
            int c = 0;
            while (n % i == 0) {
                n /= i;
                c ++;
            }
            res *= i;
            a.push_back(c);
            while (1 << m < c)
                m ++;
        }
    }
    if (n > 1) {
        res *= n;
        a.push_back(1);
    }
    for (auto x : a) {
        if (x < 1 << m) {
            m ++;
            break;
        }
    }
    cout << res << ' ' << m << endl;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    solve();

    return 0;   
}

---

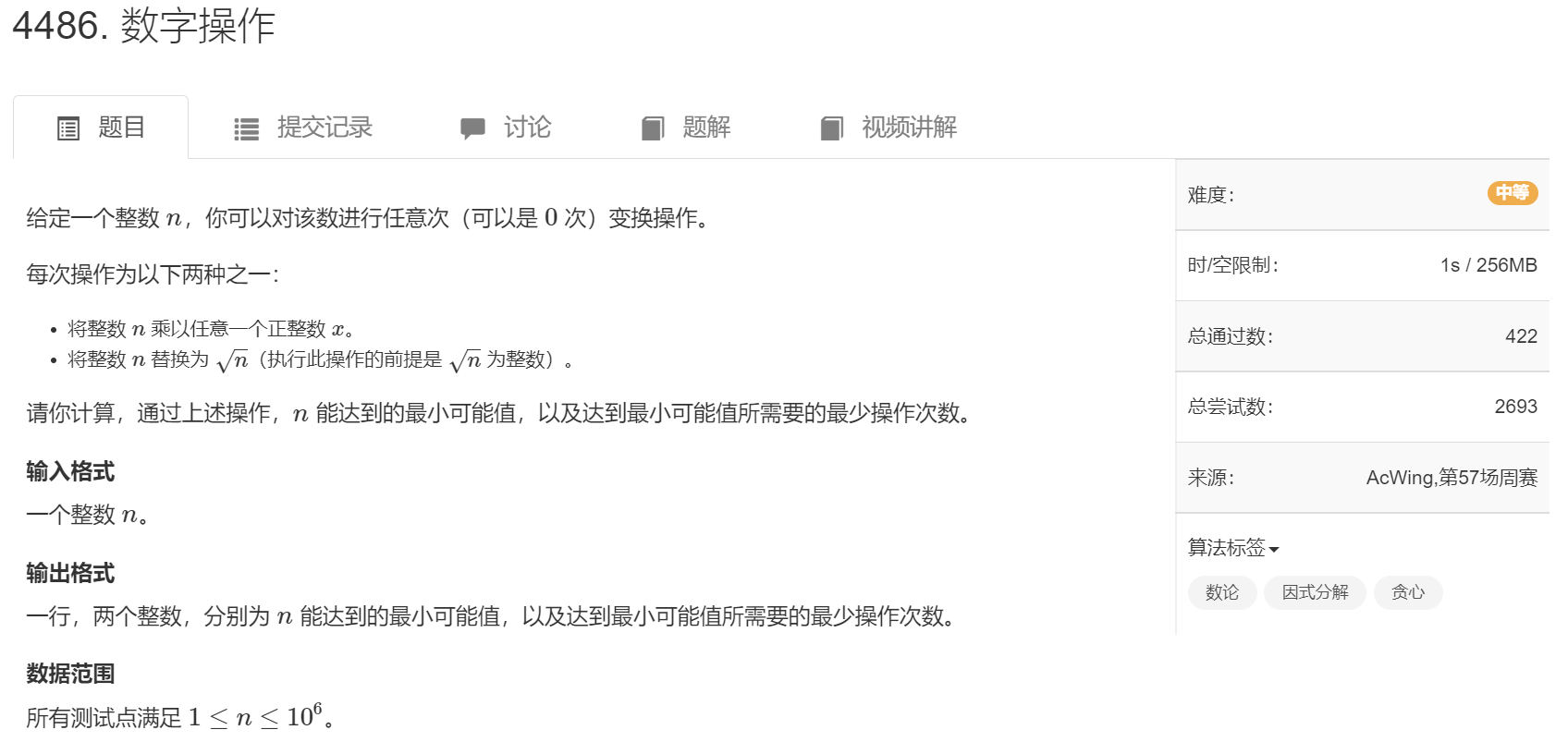
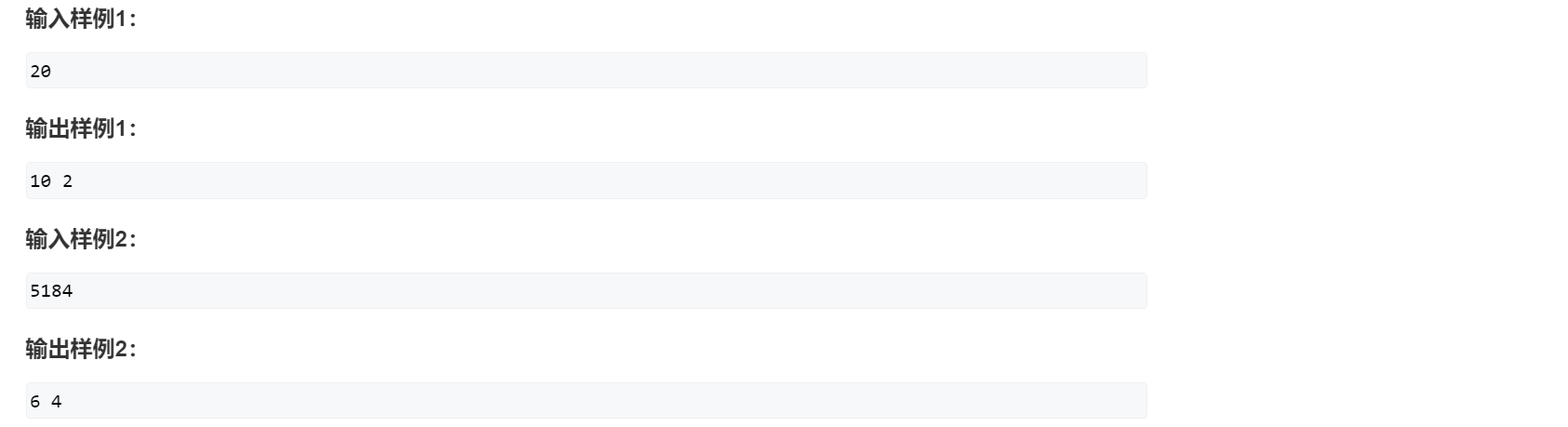
1. 最小值（数论）
   由算数基本定理，$a_i = P_1^{\alpha_1} \cdot P_2^{\alpha_2} \cdots P_k^{\alpha_k}$，所有的次方都可以通过乘一个数之后然后开方除掉，最小值即为 $P_1 \cdot P_2 \cdots P_k$
2. 最少操作次数（贪心）
   先做一次乘法，将所有因数 $P_i^{\alpha_i}$ 都变成 $P_i^{2^{m}}$ ，然后再做 $m$ 次开方，操作次数是最少的，原因如下：
   任意的 $x$（可以开方），如果先开方，得到的是 $\sqrt{x}$，然后再乘以一个 $t$，最终得到 $\sqrt{x} \cdot t$，如果采取先乘以一个 $t^{2}$，得到 $x \cdot t^{2}$，然后再开方，得到的也是 $\sqrt{x} \cdot t$
   也就是说所有先开方后乘的操作都可以用先乘后开方的操作来代替，由于乘法具有交换律，可以把所有的乘法移到算式最前面，合成一个乘法，做完这一次乘法之后再开方，一定可以保证操作次数最少