[AcWing 4 5] 多重背包问题 Ⅰ Ⅱ

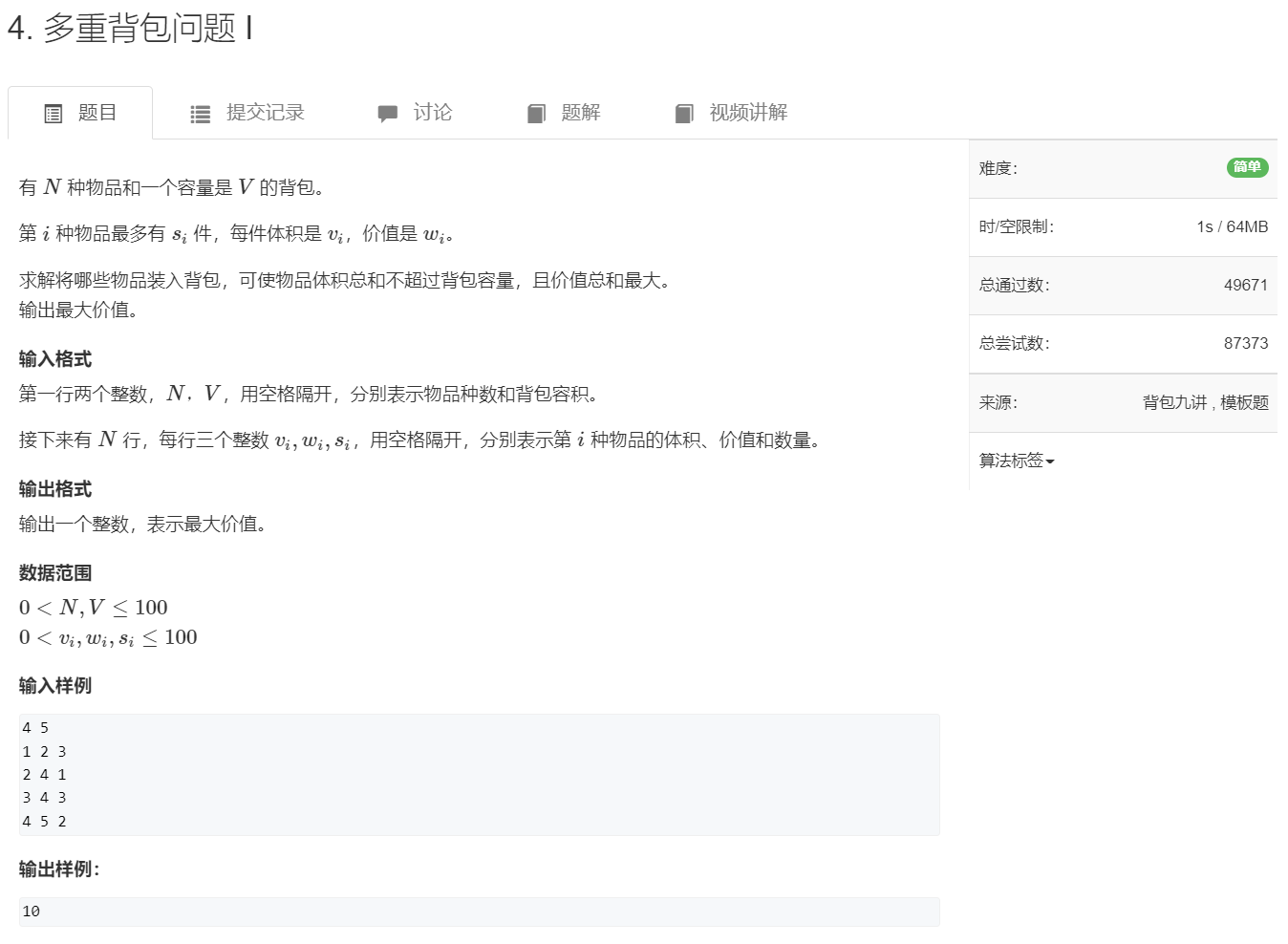
$n, v, s$ 都较小

朴素写法 时间复杂度 $n \times v \times s$

总体复杂度 $100^{3} = 1 \times 10^{6}$

---

点击查看代码

#include<iostream>

using namespace std;
const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++)   cin >> v[i] >> w[i] >> s[i];
    for (int i = 1; i <= n; i ++)
        for (int j = 0; j <= m; j ++)
            for (int k = 0; k <= s[i] && k * v[i] <= j; k ++)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    cout << f[n][m] << endl;
    return 0;
}

---

1. 和完全背包问题朴素写法很类似，$k$ 的取值范围满足 $k <= s[i] \ \ and \ \ k \cdot v[i] <= j$

---

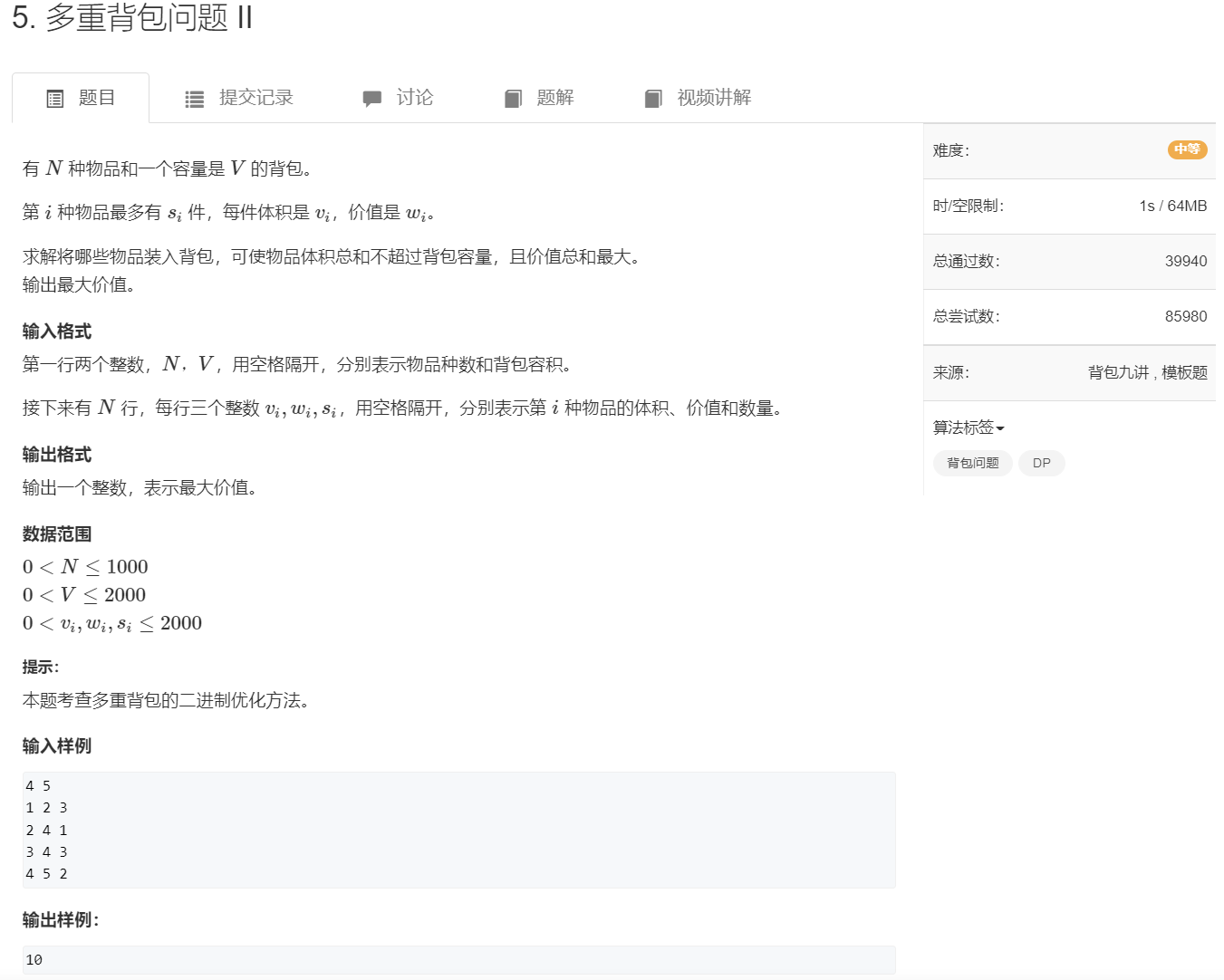
$n, v, s$ 都较大

二进制优化 复杂度 $n \times v \times log(s)$

总体复杂度 $1000 \times 2000 \times log(2000) \approx 2 \times 10^{7}$

---

点击查看代码

#include<iostream>

using namespace std;
const int N = 3e5 + 10;
int n, m;
int v[N], w[N];
int f[N];

int main()
{
    cin >> n >> m;
    int cnt = 0;
    while (n --) {
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while (k <= s) {
            cnt ++;
            v[cnt] = a * k;
            w[cnt] = b * k;
            s -= k;
            k *= 2;
        }
        if (s > 0) {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    for (int i = 1; i <= cnt; i ++)
        for (int j = m; j >= v[i]; j --)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m] << endl;
    return 0;
}

---

1. 可以把多重背包问题变为 01 背包问题
   ① 对于任意的 $s$ ，都可以拆分成 $s = 1 + 2 + 4 + \cdots + 2^{k} + c$ ，其中 $0 <= c < 2^{k + 1}$ ，因此，可以把 $s$ 拆分成若干组，也就是把每一个物品分成若干份，假设第 $i$ 份的数量为 $s_i$ ，那么第 $i$ 份的体积和价值可以表示为 $v_i^{'} = s_i \cdot v_i \ , \ w_i^{'} = s_i \cdot w_i$
   ② 使用 01 背包的思想，用一维数组优化求解