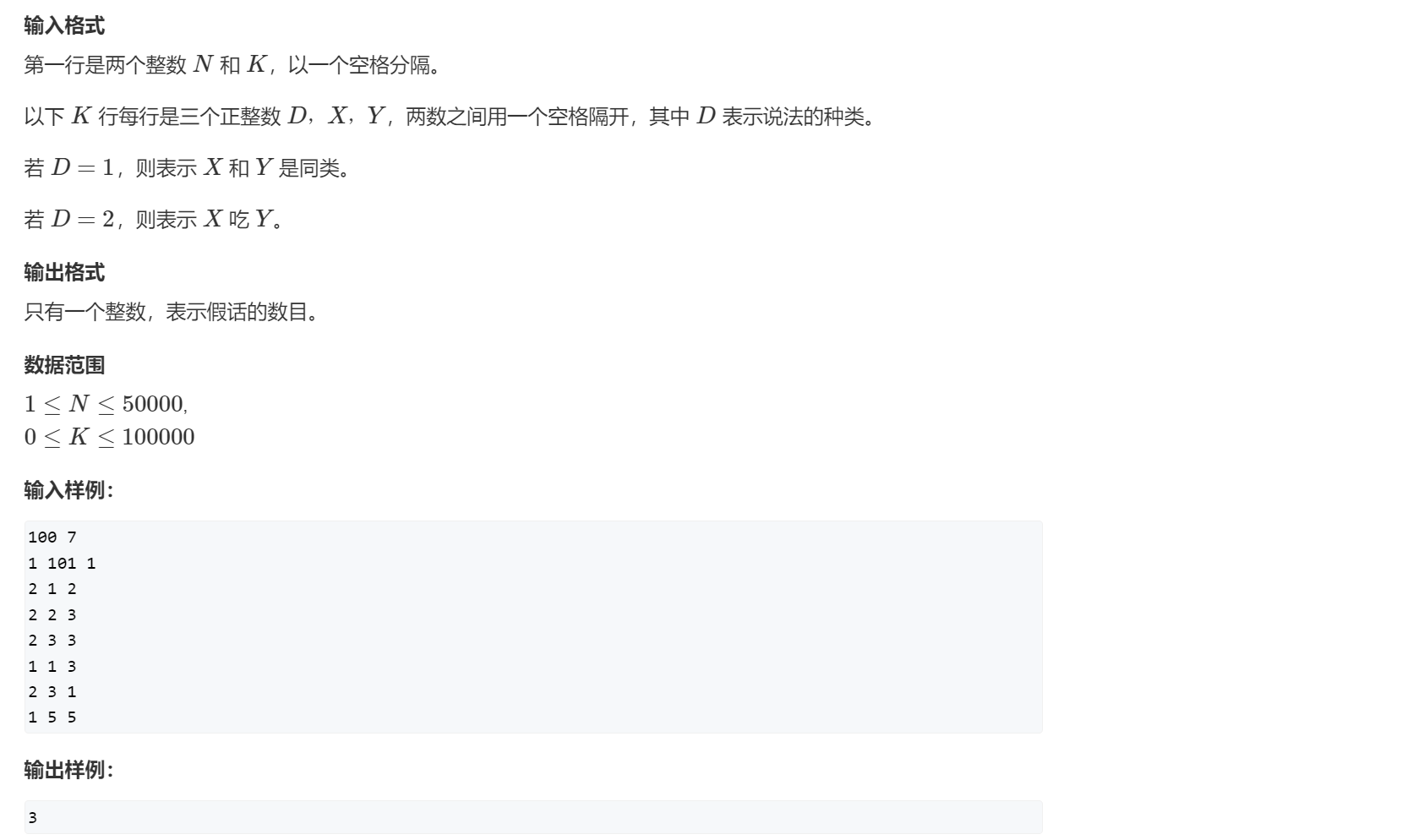
[AcWing 240] 食物链
带权并查集
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int n, m;
int p[N], d[N];
int find(int x)
{
if (p[x] != x) {
int root = find(p[x]);
d[x] += d[p[x]];
p[x] = root;
}
return p[x];
}
void merge(int a, int b, int s)
{
int pa = find(a), pb = find(b);
d[pa] = d[b] + s - d[a];
p[pa] = pb;
}
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n; i ++)
p[i] = i;
int res = 0;
while (m --) {
int t, a, b;
cin >> t >> a >> b;
if (a > n || b > n) {
res ++;
continue;
}
t --;
int pa = find(a), pb = find(b);
if (pa == pb) {
int s = d[pa] + d[a] - d[b];
if ((s % 3 + 3) % 3 != t)
res ++;
}
else
merge(a, b, t);
}
cout << res << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
solve();
return 0;
}
- 维护一个并查集的同时，记录每个节点到根节点的距离，在模 \(3\) 的意义下
① 距离为 \(0\) 表示和根节点是同类
② 距离为 \(1\) 表示可以吃根节点
③ 距离为 \(2\) 表示可以被根节点吃
仔细思考这样设置的巧妙之处，由于边权是相加的关系
① 对于 \(a\) 和 \(b\) 是同类，\(b\) 和 \(c\) 是同类，由于 \(d_{ab} = d_{bc} = 0\)，那么\(d_{ac} = 0\)，也就是 \(a\) 和 \(c\) 是同类，符合实际情况
② 对于 \(a\) 吃 \(b\)，\(b\) 吃 \(c\)，由于 \(d_{ab} = d_{bc} = 1\)，那么 \(d_{ac} = 2\)，也就是 \(a\) 被 \(c\) 吃，这符合题干中环形的食物链条件
③ 对于 \(a\) 被 \(b\) 吃，\(b\) 被 \(c\) 吃，由于 \(d_{ab} = d_{bc} = 2\)，那么 \(d_{ac} = 1\)（模 \(3\) 的情况下），也就是 \(a\) 吃 \(c\)，这符合题干中环形的食物链条件 - 判断冲突的条件：
① 说法中的 \(a\) 或 \(b\) 大于 \(n\)
② \(a\) 和 \(b\) 同属于一个集合，但 \(a\) 和 \(b\) 之间的距离不满足说法的要求（\(a\) 吃 \(a\) 这种矛盾也包含在其中，原因：\(a\) 和 \(a\) 是同类，之间的距离为 \(0\)，而 \(a\) 吃 \(a\) 这个说法，代表 \(a\) 与 \(a\) 之间的距离为 \(1\)，产生了矛盾） - 平行四边形法
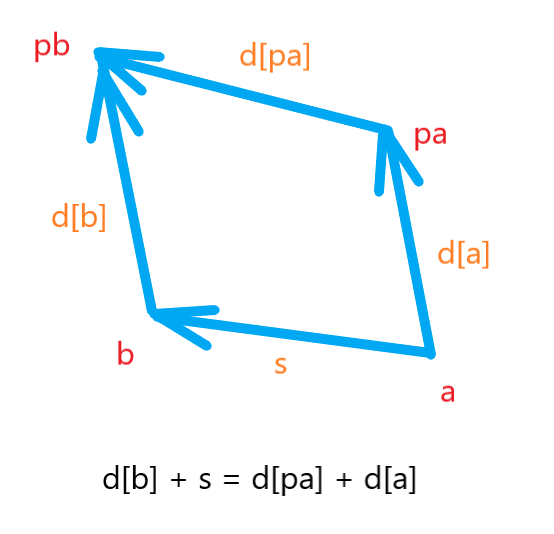
\(d[b] + s = d[pa] + d[a]\)
对于边权的计算，可以参考下图
带扩展域的并查集
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int n, m;
int p[N];
int find(int x)
{
if (p[x] != x)
p[x] = find(p[x]);
return p[x];
}
void merge(int a, int b)
{
int pa = find(a), pb = find(b);
p[pa] = pb;
}
void solve()
{
cin >> n >> m;
for (int i = 1; i <= n * 3; i ++)
p[i] = i;
int res = 0;
while (m --) {
int t, a, b;
cin >> t >> a >> b;
if (a > n || b > n) {
res ++;
continue;
}
if (a == b) {
if (t == 2)
res ++;
continue;
}
if (t == 1) {
if (find(a) == find(b + n) || find(a + n) == find(b))
res ++;
else {
merge(a, b);
merge(a + n, b + n);
merge(a + n + n, b + n + n);
}
}
else {
if (find(a) == find(b) || find(a + n) == find(b))
res ++;
else {
merge(a, b + n);
merge(a + n, b + n + n);
merge(a + n + n, b);
}
}
}
cout << res << endl;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
solve();
return 0;
}
- 可以把 \(x\)，\(y\)，\(z\) 看作是三个种类，\(x\) 吃 \(y\)，\(y\) 吃 \(z\)，\(z\) 吃 \(x\)，对于集合中的一个元素 \(p\)，\(p\) 代表 \(p\) 属于 \(x\) 类，\(p + n\) 代表 \(p\) 属于 \(y\) 类，\(p + n + n\) 代表 \(p\) 属于 \(z\) 类
- 用扩展域的方式考虑 \(a\) 和 \(b\) 是同类和 \(a\) 吃 \(b\) 这两种说法
对于 \(a\) 和 \(b\) 是同类这种说法：
① 如果 \(a\) 属于 \(x\) 类，那么 \(b\) 属于 \(x\) 类，将 \(a\) 和 \(b\) 合并集合
② 如果 \(a\) 属于 \(y\) 类，那么 \(b\) 属于 \(y\) 类，将 \(a + n\) 和 \(b + n\) 合并集合
③ 如果 \(a\) 属于 \(z\) 类，那么 \(b\) 属于 \(z\) 类，将 \(a + n + n\) 和 \(b + n + n\) 合并集合
对于 \(a\) 吃 \(b\) 这种说法：
① 如果 \(a\) 属于 \(x\) 类，那么 \(b\) 属于 \(y\) 类，将 \(a\) 和 \(b + n\) 合并集合
② 如果 \(a\) 属于 \(y\) 类，那么 \(b\) 属于 \(z\) 类，将 \(a + n\) 和 \(b + n + n\) 合并集合
③ 如果 \(a\) 属于 \(z\) 类，那么 \(b\) 属于 \(x\) 类，将 \(a + n + n\) 和 \(b\) 合并集合 - 判断冲突的条件：
① 说法中的 \(a\) 或 \(b\) 大于 \(n\)
② 说法中，\(t = 2\)，但 \(a = b\)
③ \(t = 1\) 时，\(a\) 和 \(b + n\) 在同一集合（代表 \(a\) 吃 \(b\)），或者 \(a + n\) 和 \(b\) 在同一集合（代表 \(a\) 被 \(b\) 吃）
③ \(t = 2\) 时，\(a\) 和 \(b\) 在同一集合（代表 \(a\) 和 \(b\) 是同类），或者 \(a + n\) 和 \(b\) 在同一集合（代表 \(a\) 被 \(b\) 吃）
