蛮力法求矩形个数

给定n*n的矩阵，矩阵中有0和1两个数字，现要求矩阵中只包含0的矩形的数量。
枚举矩形左上角坐标𝑖,𝑗，矩形右边界𝑘，在𝑖,𝑗,𝑘一定的情况下能得到的满足条件的矩形个数和能向下扩展的高度有关，在𝑘增加的过程中不断更新可扩展的高度。
矩阵中数字如下，求矩阵中只包含0的矩形的数量。
0 0 1 0
1 1 0 1
0 1 0 0
0 1 0 1

因此我们只要预处理出每个位置能向下扩展的最高高度h[i][j]，
再在枚举k的时候取min{h[i][j], h[i][j + 1], ……, h[i][k]},即可以得到矩形的个数。

最终求得问题所示的矩阵中包含15个矩形。

分析：
对十六个节点从上到下，从左到右能扩展得到的矩形个数相加。

#include<iostream>
#define MAX 100
using namespace std;
//int ans = 10000;
int mp[MAX][MAX];
int h[MAX][MAX];
int m,n;
void disp()
{
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
           cout<<h[i][j]<<" ";
        }
        cout<<endl;
    }
}
int fun()
{
    for(int i=n;i>=1;i--)//从下到上预处理每个位置可以向下扩展的最高高度
    {
        for(int j=1;j<=n;j++)
        {
            if(mp[i][j])
                h[i][j]=0;
            else
                h[i][j]=h[i+1][j]+1;
        }
    }
    int ans =0;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            int hei = h[i][j];//可扩展的高度
            for(int k=j;k<=n;k++)
            {
                hei=min(h[i][k],hei);//可扩展的高度由最小值决定
                ans+=hei;
                //cout<<i<<" , "<<k<<"  j= "<<j<<"  hei    " <<hei<<endl;
            }
            //cout<<"ans: " <<ans<<endl;
        }
    }
    return ans;
}
int main()
{
    //freopen("C:\\in.txt","r",stdin);
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            cin>>mp[i][j];
        }
    }

    cout<<fun();
    //cout<<endl;
    //disp();

}

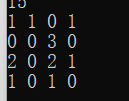
预处理得到的h[][]为

输出每一次hei的值

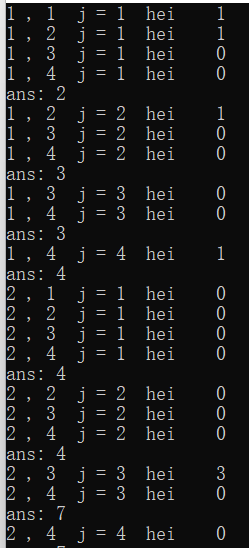
分析j=1 -> j=4 的第一次完整过程，即处理第一行
可以这样理解：j=1时，计算的是，第一行每个节点可以往下延伸得到的矩形个数，
j=2.3.4时，既是可以从mp[1][1]节点向右延伸得到的矩形个数
对于 hei=min(h[i][k],hei);的理解：
如h的分块矩阵为：
1 2
0 1
那么既是第二列两个都是0，由于前一列，一个为0，一个为1，则只能向右延伸一位
如果为：
2 2
1 1
则毫无疑问该田字格状mp[2][2]为
0 0
0 0
即可以往右形成两个组合矩形
（1）
0 0
（2）
0 0
0 0
如果中间出现一次0，即说明该点mp[i][k]与mp[i][j]点不再连通，记为0（该点本身为1）或1（该点本身为0）。
由此得到矩形个数。