洛谷P2365/acwing102(单调队列，斜率优化)

洛谷P2365
n个任务排成一个序列在一台机器上等待完成（顺序不得改变），这n个任务被分成若干批，每批包含相邻的若干任务。
从零时刻开始，这些任务被分批加工,第i个任务单独完成所需的时间为ti。在每批任务开始前，机器需要启动时间s,而完成这批任务所需的时间是各个任务需要时间的总和（同一批任务将在同一时刻完成）。
每个任务的费用是它的完成时刻乘以一个费用系数fi。请确定一个分组方案，使得总费用最小。
大概就是题解第一说的这样（厚颜无耻地搬了）

//
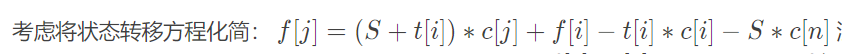
// Created by vv123 on 2022/2/22.
//
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 5010;
int dp[N], t[N], f[N], q[N], s, n, l, r;
signed main() {
    cin >> n >> s;
    for (int i = 1; i <= n; i++) {
        cin >> t[i] >> f[i];
        t[i] += t[i - 1];
        f[i] += f[i - 1];
    }
    memset(dp, 0x3f, sizeof(dp));
    dp[0] = 0;
    //维护一段斜率单调增的折线
    //一个斜率单增的直线取最小截距，排除斜率小于它的折线段，每次从队首转移
    l = 1, r = 0;
    q[0] = 0, r++;
    for (int i = 1; i <= n; i++) {
        while (l < r && (s + t[i]) * (f[q[l+1]] - f[q[l]]) >= dp[q[l+1]] - dp[q[l]]) l++;
        dp[i] = dp[q[l]] + t[i] * f[i] + s * f[n] - (s + t[i]) * f[q[l]];
        while (l < r && (dp[i] - dp[q[r]]) * (f[q[r]] - f[q[r-1]]) <= (dp[q[r]] - dp[q[r-1]]) * (f[i] - f[q[r]])) r--;
        q[++r] = i;
    }
    cout << dp[n] << endl;
    return 0;
}

acwing102

//
// Created by vv123 on 2022/2/22.
//
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int s[N], q[N];
double slope(int i, int j) {
    return (double) (1.0 * s[i] - s[j]) / (i - j);
}
int main() {
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        cin >> s[i];
        s[i] += s[i - 1];
    }
    int l = 1, r = 0;
    double ans = 0;
    for (int i = m; i <= n; i++) {
        //维护上凸包，选择队首
        while (l < r && slope(i - m, q[r]) <= slope(q[r], q[r - 1])) r--;
        q[++r] = i - m;
        while (l < r && slope(i, q[l]) <= slope(i, q[l+1])) l++;
        ans = max(ans, slope(i, q[l]));
    }
    cout << (int) (ans * 1000);
    return 0;
}