Codeforces Round #686 (Div. 3) E.ArrayPartition

Codeforces Round #686 (Div. 3) E.ArrayPartition

题目大意：找到x、y、z三个数，将数组分成3部分，使得第一部分的最大值、第二部分的最小值、第三部分的最大值全部相等。

思路

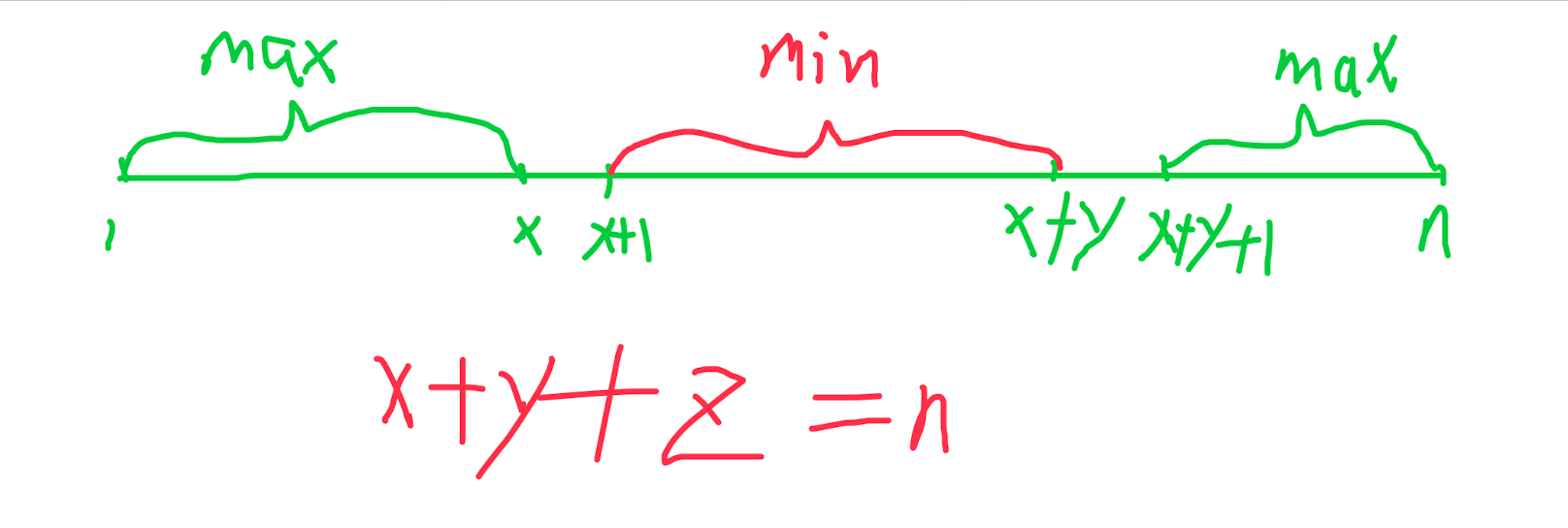
查询区间的最值，但并不修改数组，这使我们想到了ST表这个数据结构，可以O(nlogn)的预处理，O(1)进行查询区间最值，本题需要维护两个ST表来分别查询最大值和最小值。

接下来可以枚举第一个区间的右端点x位置，当固定x后，随着中间区间右端点的增大，中间部分的最小值具有非降序的性质；同理可得随着中间部分右端点的增大，第三部分的最大值具有非升序的性质，这使我们联想到了二分查找，解决具有单调性的问题。所以：

1. 枚举第一个区间右端点x的位置
2. 在1的情况下二分出第二部分右端点的上限和下限。
3. 在第2步得到的上限和下限区间中，再次二分第三部分的左端点。

代码

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

constexpr int N = 2e5 + 5;
int a[N];
int stMin[N][20];
int stMax[N][20];

// 构建ST表
void build(int n)
{
    for(int i = 1; i <= n; i++) stMin[i][0] = stMax[i][0] = a[i];
    for(int k = 1; (1 << k) <= n; k++)
        for(int i = 1; i + (1 << k) - 1 <= n; i++)
        {
            stMin[i][k] = min(stMin[i][k - 1], stMin[i + (1 << (k - 1))][k - 1]);
            stMax[i][k] = max(stMax[i][k - 1], stMax[i + (1 << (k - 1))][k - 1]);
        }
}

int query_max(int l, int r)
{
    int d = log2(r - l + 1);
    return max(stMax[l][d], stMax[r - (1 << d) + 1][d]);
}
int query_min(int l, int r)
{
    int d = log2(r - l + 1);
    return min(stMin[l][d], stMin[r - (1 << d) + 1][d]);
}

int main()
{
    cin.tie(nullptr);
    int t;
    cin >> t;
    while(t--)
    {
        int n;
        cin >> n;
        for(int i = 1; i <= n; i++) cin >> a[i];
        build(n);
        bool flag = false;
      	// 枚举第一个区间的右端点x -> i
        for(int i = 1; i < n - 1; i++)
        {
            int target = query_max(1, i);	// 第一部分的最大值，作为二分的条件
            int l = i + 1, r = n - 1;			// 第二部分的右端点[i+1, n-1]
          	// 二分第二部分右端点的下界
            while(l < r)
            {
                int mid = (l + r) >> 1;
                if(query_min(i + 1, mid) <= target) r = mid;
                else l = mid + 1;
            }
            if(query_min(i + 1, l) != target) continue;
            int ll = l;
            l = i + 1, r = n - 1;
          	// 二分第二部分右端点的上界
            while(l < r)
            {
                int mid = (l + r + 1) >> 1;
                if(query_min(i + 1, mid) >= target) l = mid;
                else r = mid - 1;
            }
            int rr = l;
            l = ll + 1, r = rr + 1;				// 第三部分的左端点[ll+1, rr+1]
          	// 二分第三部分的左端点
            while(l < r)
            {
                int mid = (l + r) >> 1;
                if(query_max(mid, n) <= target) r = mid;
                else l = mid + 1;
            }
            if(query_max(l, n) == target)
            {
                cout << "YES\n";
                cout << i << " " << l - i - 1 << " " << n - l + 1 << "\n";
                flag = true;
                break;
            }
        }
        if(!flag) cout << "No\n";
    }
}

解决本题的关键是找到题目中隐含的单调性，从而采用二分去优化,使得时间复杂度降到O(nlogn)，不然暴力的方法(O(n^3)根本通不过。要注意好多边界问题，我也调试了大概半个多小时，才运行成功，总之要细心。