SVM学习——软间隔优化
回想SVM学习——线性学习器一文中提到的Rosenblatt感知器的原始形式,当时的讨论是基于输入空间线性可分的情况,包括后来的最大间隔算法,通过核函数隐式的将输入空间映射到了一个高维特征空间中了,此时的假设同样是映射后的数据线性可分,那自然就会想到如果输入空间或者由核函数映射得到的特征空间依然是线性不可分的可怎么办呀?这个时候以前的算法一定是不收敛的,对,它会不停的振荡;由SVM学习——求解二次规划问题一文中提到的最大间隔算法的K-T互补条件,我们已经了解到一个信息:支持向量包括了所有重构超平面的必要信息,就算其他点不要了也能得到这个超平面,而支持向量越少,泛化能力越强,另外,由SVM学习——统计学习理论一文中关于学习器推广能力的界的讨论可以知道界的良好性能在于它不与特征空间的维度显式相关,从最大间隔算法本身来看并没有控制支持向量数目的痕迹,一切都是基于样本数据的,该算法唯一的自由度体现在对核函数的选择,但是用很强的核将数据分开又可能导致过拟合发生;前面说到的振荡情况,其实是该算法对噪声点过于敏感的体现,换句话说,最大间隔算法想过于完美的将数据进行无误差的训练,在现实当中,由于存在噪声,所以这样的想法其实是不符合实际的, 这可能是整个学习器受制于个别几个点,于是引出软间隔优化,顾名思义,它的出现想要解决前面的问题,使训练器能容忍噪声的同时顾及到更多的样本。
先了解一下间隔分布的另一个度量方法,它将间隔的概念从最靠近超平面的点推广到了所有训练集数据,因此更能说明训练样例的全局特性 。
定义1:设为目标间隔,且
,任意一个输入样本
对应于超平面
和目标间隔
的松弛变量是:
这个定义很有意思,当样本没有被误分时,为正,因此,
,当样本被误分时
为负,
,于是
就描述了训练集中没有以间隔
分开以及误分的情况,例如,经典二分类SVM中,设定
,则
,当样本被误分或者没有以间隔
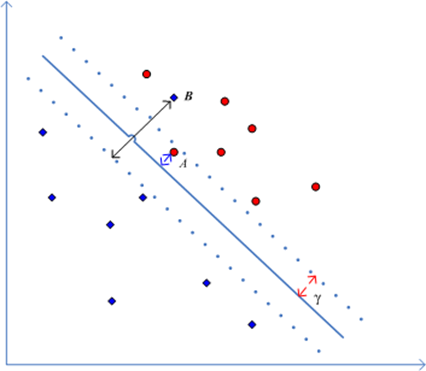
分开时,其松弛变量不为零,而没有被误分时,其松弛变量为0,如图所示:
图中除了A、B两点以外的点,松弛变量都为0,点A是一个没有以间隔分开的样例,而点B是被误分的样例,它们的松弛变量都不为零。
对原始最大间隔优化问题引入上面的松弛变量,可以将约束转变为:
对于原问题的形式,有如下两种:二阶范数软间隔和一阶范数软间隔。
1、二阶范数软间隔
原始问题为:
其中
叫做惩罚因子,
就是松弛变量了
推导一下下:原问题的拉格朗日函数为:
于是有:
让上三式都等于0,得到下面的对偶目标函数:
总结一下,用核函数替换内积得到:
其中
求得最优解后得到的几何间隔为:
可以看到C的选取影响到最终的间隔,C越大,说明对噪声点越重视,因此噪声点的影响变大,最后求得的几何间隔就越大。
2、一阶范数软间隔
原始问题为:
其中
为惩罚因子,
为松弛变量
原问题的拉格朗日函数为:
处理方法类似,得到:
让上三式都等于0,得到下面的对偶目标函数:
用核函数替换内积得到:
求得最优解后得到的几何间隔为:
我晕,和以前的最大间隔算法中的对偶形式一样,仅多了一个约束,也就是此时的K-T互补条件是:
从上面式子可以得到的信息是:当时,松弛变量
不为零,此时其几何间隔小于
,对应样本点就是误分点;当
时,松弛变量
为零,此时其几何间隔大于
,对应样本点就是内部点,即分类正确而又远离最大间隔分类超平面的那些样本点;而
时,松弛变量
为零,此时其几何间隔等于
,对应样本点就是支持向量。
的取值一定是
,这意味着向量
被限制在了一个 边长为C的盒子里,神奇吧,嘿嘿。
到底使用一阶范数软间隔还是二阶范数软间隔取决于数据情况。
关于惩罚因子C的作用可以用下面的图来说明,使用的工具是libsvm,采用线性核函数,除了惩罚因子外其它参数默认:
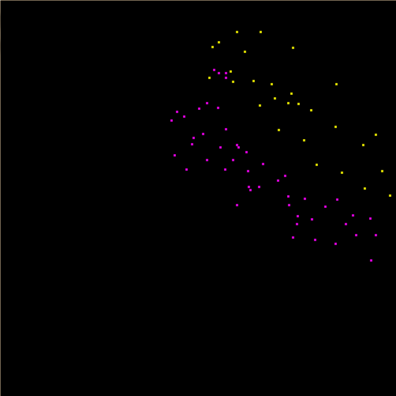
1、原始数据分布:
可以看到有四个粉色的点离群的比较离谱,我们基本可以认为它们是噪声点了。
2、惩罚因子取值为
2、惩罚因子取值为
2、惩罚因子取值为
这几个图说明啥子问题呢?C越大表明你越不想放弃离群点,分类超平面越向离群点移动,于是最终的分类超平面就越容易被离群点给掌控喽。
关于libsvm,现在应该是3.0版本了,可以从http://www.csie.ntu.edu.tw/~cjlin/libsvm/index.html 的Download LIBSVM这一小节的得到,有两个版本,一个是Windows下的,一个是Linux下的,这里面包含源码哦,可以好好研究一下。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号