CF102411 ICPC 2019-2020 North-Western Russia Regional Contest题解
A Accurate Movement
签到
M Managing Difficulties
签到
B Bad Treap
已知\(y=\sin(x)\),要求给出数组\(a[n]\),满足\(\forall i,j\in[1,n],a[i]\neq a[j]\),都有\(\sin(a[i])\neq \sin(a[j])\)。
这里又一种不怎么玄的写法,就是我们找到一个整数\(x\),\(sin(x)\)非常非常小并且\(\sin(x)>0\),这样算,嗯……例如\(sin(2x)\)的时候,\(\sin(2x)=2\sin x \cos x\),它的值只会有很小的增加\((2\cos x<2)\)。然后就算它扩大了\(2.5\times10^4\)倍之后,仍然都增加不到接近1的位置,那么我们就成功了。然后因为\(\sin x\)关于原点对称,在负半轴把它对称过去,仍然是一个递增序列。
int n;
const int N = 5e4 + 5;
int a[N];
int main(void){
scanf("%d", &n);
double mn = 100;
int id = 1;
for (int i=1;i<=4e4;++i){
if (sin(i) < mn && sin(i) > 0){
mn = sin(i), id = i;
}
}
for (int i=-25000;i<=25000;++i){
a[i + 25000] = i * id;
}
for (int i=0;i<n;++i){
printf(i==n-1?"%d\n":"%d ", a[i]);
}
return 0;
}
不对称过去会wa7,(露西亚,你太baby辣)
I Ideal Pyramid
给定\(n\)个方尖碑,要用一个仰角为45°的金字塔把它们全部覆盖起来,也就是建成金字塔之后,所有的方尖碑都会被它掩盖,高度也不会穿过金字塔,问金字塔应该建在哪里,高度最小为多少。
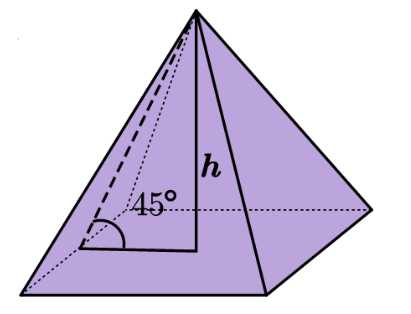
实际上,所有的四棱锥都可以转化为一个正方形的覆盖,那么题意就转化为了,找到一个最小的正方形,可以包括所有的正方形的集合。这样的话,直接维护正方形集合的上下左右边界(最后得到一个矩形),再按照矩形的中心扩展即可。
int n;
const int N = 1000 + 5;
void solve(){
n = read();
ll x, y, h;
ll L = 1e18, R = -1e18, U = -1e18, D = 1e18;
for (int i=1;i<=n;++i){
x = read(), y = read(), h = read();
L = min(L, x - h), R = max(R, x + h), U = max(U, y + h), D = min(D, y - h);
}
ll a = (L + R) / 2, b = (U + D) / 2, H = max((R - L + 1) / 2, (U - D + 1) / 2);
printf("%lld %lld %lld\n", a, b, H);
}
int main(void){
int T;
// T = read();
T = 1;
while (T--){
solve();
}
return 0;
}
King's Children
有一个\(n\times m\)的网格,里面有最多\(A~to ~Z\)个孩子,king要把这个网格分成若干矩形,要满足:
- 每个矩形必须精确的包括一个孩子
- 每个格子都必须精确的属于1个矩形(也就是矩形不相交的分完整个大网格)
- 包括了\(A\)的矩形的面积尽可能大
数据范围\(1\leq n,m\leq 1000\)
这题可以用悬线法,也可以用单调栈(不如说悬线法就是单调栈的一个子集问题)
算是比较经典的求最大子矩形的问题,然而我不会,下面先介绍一下悬线法。
悬线法
oi-wiki的定义:https://oi-wiki.org/misc/hoverline/
一个简单的题目,简单理解悬线法的过程:
SP1805 Largest Rectangle in a Histogram
https://www.luogu.com.cn/problem/SP1805
首先,\(n\)个矩形就相当于\(n\)条悬线,我们知道最大的面积肯定是由某一个悬线向左右扫过而形成的。那么悬线的扩展,显然的满足某一递推关系,可以帮助我们将复杂度由原来的\(O(N^2)\)变成\(O(N)\)。
定义\(l_i\)为当前的\(i\)位置能扩展到的悬线的最左端,初始时\(l_i=i\)。假设已经处理好了前\(i-1\)个位置的答案,那么当\(h_i\leq h_{i-1}\)时,\(i\)也能扩展到\(i-1\)能扩展到的位置。如果\(h_i\leq h_{l_{i-1}-1}\)时,又可以接着往前扩展……直到扩展到边界,我们就停止。因此对于\(\forall i\),我们有
while (L[i] > 1 && a[i] <= a[L[i] - 1]) L[i] = L[L[i] - 1];
同样的,假如我们已经处理好\(i+1\)到\(n\)的答案,\(r_i\)也能不断的向右扩展。
while (R[i] < n && a[i] <= a[R[i] + 1]) R[i] = R[R[i] + 1];
那么完整代码:
int n;
const int N = 1e5 + 5;
int a[N], L[N], R[N];
void solve(){
for (int i=1;i<=n;++i){
scanf("%d", &a[i]);
L[i] = R[i] = i;
}
for (int i=1;i<=n;++i){
while (L[i] > 1 && a[i] <= a[L[i] - 1]) L[i] = L[L[i] - 1];
}
for (int i=n;i>=1;--i){
while (R[i] < n && a[i] <= a[R[i] + 1]) R[i] = R[R[i] + 1];
}
ll res = 0;
for (int i=1;i<=n;++i){
res = max(res, 1LL * a[i] * (R[i] - L[i] + 1));
}
printf("%lld\n", res);
}
UVA1619/POJ2796 Feel Good
给出长度为\(n\)的数组\(a[n]\),找到一个子区间,使得子区间内的最小值与区间内所有元素和的乘积最大,如果有多个答案,输出长度最小的答案,如果仍有多个答案,输出最左端序号最小的答案。
枚举这个最小值,它一旦向左右扩展,就肯定会增加这个乘积的值,这样的话,又变成了一个悬线法求最大子矩形的问题。
数据范围:\(1\leq n \leq 10^5\) 我恨UVA的多组数据和格式
int n;
const int N = 1e5 + 5;
int a[N], L[N], R[N];
ll pre[N];
bool fst = 1;
void solve(){
// n = read();
if (!fst){
puts("");
}
fst = 0;
for (int i=1;i<=n;++i){
a[i] = read();
pre[i] = pre[i - 1] + a[i];
L[i] = R[i] = i;
}
for (int i=1;i<=n;++i){
while (L[i] > 1 && a[i] <= a[L[i] - 1]) L[i] = L[L[i] - 1];
}
for (int i=n;i>=1;--i){
while (R[i] < n && a[i] <= a[R[i] + 1]) R[i] = R[R[i] + 1];
}
ll res = 0;
int aL = 1, aR = 1;
for (int i=1;i<=n;++i){
ll cur = (pre[R[i]] - pre[L[i] - 1]) * a[i];
if (cur > res){
res = cur, aL = L[i], aR = R[i];
}
else if (cur == res){
if (R[i] - L[i] < aR - aL){
aL = L[i], aR = R[i];
}
else if (R[i] - L[i] == aR - aL){
if (L[i] < aL){
aL = L[i], aR = R[i];
}
}
}
}
printf("%lld\n%d %d\n", res, aL, aR);
}
int main(void){
while (~scanf("%d", &n)){
if (n == 0){
puts("");
}
else solve();
}
return 0;
}
最大子矩形:p4147 玉蟾宫
嗯……差不多捏,问题。oiwiki留的课后习题也写了,就不放出来了。
那么正式说K,K题我的思路就是,每个矩形都用悬线法进行选取和填充。但是,由于填充顺序的不同,有极低的概率出现最后有矩形没有被完全填上的情况,因此做一个简单的check,如果填充错误,则随机化顺序,重新填充答案。大概2~3次随机后就不可能出现还没填充的情况了,所以这个复杂度是完全可行的。
代码:
int n, m, sx, sy;
const int N = 1000 + 5;
char s[N][N], ss[N][N];
int U[N], L[N], R[N];
struct node{
char ch;pii cor;
};
vector<node> alp;
bool check(pii s, pii a, pii b){
return (s.xx >= a.xx && s.xx <= b.xx) && (s.yy >= a.yy && s.yy <= b.yy);
}
void putin(char ch, pii cor){
int res = 0; pii r1 = cor, r2 = cor;
for (int j=1;j<=m;++j) U[j] = 0;
for (int i=1;i<=n;++i){
for (int j=1;j<=m;++j){
if (s[i][j] == '.' || s[i][j] == ch){
U[j]++;
}
else{
U[j] = 0;
}
L[j] = R[j] = j;
}
for (int j=1;j<=m;++j){
while (L[j] > 1 && U[j] <= U[L[j] - 1]) L[j] = L[L[j] - 1];
}
for (int j=m;j>=1;--j){
while (R[j] < m && U[j] <= U[R[j] + 1]) R[j] = R[R[j] + 1];
}
for (int j=1;j<=m;++j){
int cur = U[j] * (R[j] - L[j] + 1);
pii c1 = pii(i - U[j] + 1, L[j]), c2 = pii(i, R[j]);
if (cur > res && check(cor, c1, c2)){
res = cur, r1 = c1, r2 = c2;
}
}
}
for (int i=r1.xx;i<=r2.xx;++i){
for (int j=r1.yy;j<=r2.yy;++j){
if (s[i][j] == '.'){
s[i][j] = 'a' + (ch - 'A');
}
}
}
}
void solve(){
for (int i=1;i<=n;++i){
for (int j=1;j<=m;++j){
s[i][j] = ss[i][j];
}
}
int alen = alp.size(), t = alen - 1;
if (alen > 1){
for (int i=0;i<alen-1;++i){
int x = 1 + rand() % t;
swap(alp[x], alp[t]);
t--;
}
}
for (int i=0;i<alp.size();++i){
putin(alp[i].ch, alp[i].cor);
}
}
bool isOK(){
for (int i=1;i<=n;++i){
for (int j=1;j<=m;++j){
if (s[i][j] == '.'){
return false;
}
}
}
return true;
}
int main(void){
srand(time(NULL));
int T;
T = 1;
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
cin >> n >> m;
for (int i=1;i<=n;++i){
for (int j=1;j<=m;++j){
cin >> ss[i][j];
if (ss[i][j] == 'A'){
alp.push_back(node{'A', pii(i, j)});
}
}
}
for (int i=1;i<=n;++i){
for (int j=1;j<=m;++j){
if (ss[i][j] != '.' && ss[i][j] != 'A'){
alp.push_back(node{ss[i][j], pii(i, j)});
}
}
}
do{
solve();
}while(!isOK());
for (int i=1;i<=n;++i){
for (int j=1;j<=m;++j){
cout << s[i][j];
}
cout << endl;
}
return 0;
}
E Equidistant
给出一个树,判断是否有一个结点,满足到所有特殊点的距离相等。
数据范围:\(1\leq m,n\leq 2\times 10^5\)。
这题感觉用多源bfs更简单……嗯……用树形DP试着写写吧。
树形DP 不推荐。。。。
int n, m;
const int N = 2e5 + 5, INF = 1e9 + 10;
bool st[N], ok;
vector<int> ve[N];
int f[N], g[N];
void dfs(int u, int pre){
for (auto to : ve[u]){
if (to == pre) continue;
dfs(to, u);
f[u] = min(f[u], f[to] + 1);
g[u] = max(g[u], g[to] + 1);
}
}
void dfs2(int u, int pre){
if (ok) return;
if (f[u] == g[u]){
if (!ok){
puts("YES");
printf("%d\n", u);
}
ok = true;
return ;
}
int mx1 = -INF, mx2 = -INF, mn1 = INF, mn2 = INF;
if (st[u]){
mx1 = mn1 = 0;
}
for (auto to : ve[u]){
if (f[to] + 1 < mn1){
mn2 = mn1, mn1 = f[to] + 1;
}
else if (f[to] + 1 < mn2){
mn2 = f[to] + 1;
}
if (g[to] + 1 > mx1){
mx2 = mx1, mx1 = g[to] + 1;
}
else if (g[to] + 1 > mx2){
mx2 = g[to] + 1;
}
}
for (auto to : ve[u]){
if (to == pre) continue;
int fto = f[to], gto = g[to];
if (f[u] == f[to] + 1){
f[u] = mn2;
f[to] = min(f[to], mn2 + 1);
}
else{
f[to] = min(f[to], f[u] + 1);
}
if (g[u] == g[to] + 1){
g[u] = mx2;
g[to] = max(g[to], mx2 + 1);
}
else g[to] = max(g[to], g[u] + 1);
dfs2(to, u);
f[u] = mn1, g[u] = mx1;
f[to] = fto, g[to] = gto;
}
}
int main(void){
n = read(), m = read();
for (int i=1;i<=n;++i){
f[i] = INF, g[i] = -INF;
}
int u, v, x;
for (int i=1;i<n;++i){
u = read(), v = read();
ve[u].push_back(v), ve[v].push_back(u);
}
for (int i=1;i<=m;++i){
x = read(), st[x] = true;
f[x] = g[x] = 0;
}
dfs(1, 0);
dfs2(1, 0);
if (!ok){
puts("NO");
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号