abc292[AtCoder Beginner Contest 292] 题解

写点题目转换下心情吧

A-CAPS LOCK

大水题

B-Yellow and Red Card

大水题

C-Four Variables

给定一个数\(N\)，问有多少个有序正数数组\((A,B,C,D)\)，满足\(A\times B+C\times D=N\)。

这题荒芜的大脑拒绝思考，看着复杂度不超，写了\(O(N\sqrt N)\)结束了。思想很简单，就是把\(N\)分成两个正整数\(x,y\)，再\(O(\sqrt N)\)找因数，最后把\(x,y\)的因数数量相乘。

知道有\(O(N\log N)\)的算法，但是瞬间能写出来的只有这个简单版的了，要反思（）

int n;
const int N = 2e5 + 5;
int a[N];

int getNum(int x){
    if (a[x] != 0) return a[x];
    int num = 0;
    for (int i = 1;i * i <= x; ++i){
        if (x % i == 0){
            int j = x / i;
            num++;
            if (i != j) num++;
        }
    }
    return a[x] = num;
}

int main(void){
    cin >> n;
    ll sm = 0;
    for (int i=1;i<n;++i){
        int t1 = getNum(i);
        int t2 = getNum(n - i);
        sm = sm + 1LL * t1 * t2;
    }
    cout << sm << endl;
    return 0;
}

那现在回忆一下\(O(\log N)\)的int getNum(int x)吧，冷静下来想想直接写个类似埃式筛的东西就可以。

void init(){
    for (int i=1;i<=n;++i){
        for (int j=1;1LL * i * j <= n;++j){
            f[i * j]++;
        }
    }
}

D-Unicycliv Components

给定一个\(n\)个结点\(m\)条边的无向图，问是否每个连通块都满足它的点数和边数相同。

嗯……这题一开始看错题目了，然后耽误了很久写的很麻烦。后面发现对不上样例（典）然后发现这题实际的题意挺简单的。正常查连通块有多少点，然后累加它们的度\(d_i\)，那么连通块边数就等于\(\frac{\sum d_i}{2}\)。图论稀碎的我也就这点本事了qaq

int n, m;
const int N = 2e5 + 10, M = 2e5 + 10;
int deg[N];
vector<int> ve[N];
int edges = 0, vertices = 0;
bool vis[N];

void dfs(int x){
    int len = ve[x].size();
    vis[x] = true, vertices++, edges += deg[x];
    for (int i : ve[x]){
        if (!vis[i]) dfs(i);
    }
}

int main(void){
    int u, v;
    cin >> n >> m;
    for (int i=1;i<=m;++i){
        cin >> u >> v;
        deg[u]++, deg[v]++;
        ve[u].push_back(v), ve[v].push_back(u);
    }
    for (int i=1;i<=n;++i){
        vertices = edges = 0;
        if (!vis[i]) dfs(i);
        if (vertices << 1 != edges){
            cout << "No" << endl;
            return 0;
        }
    }
    cout << "Yes" << endl;
    return 0;
}

E-Transitivity

给定一个\(n\)个结点\(m\)条边的有向简单图，对于任意一个三元组\((a,b,c)\)，可执行操作\(x\)：若存在边\(a\rightarrow b\)，存在边\(b \rightarrow c\)，且不存在边\(a\rightarrow c\)，那么就可以手动加上\(a\rightarrow c\)这条边。问最少要加多少条边才能使得无法再执行该操作。

数据范围：\(3\leq N \leq 2000;0\leq M \leq 2000;1\leq u_i,v_i\leq N;u_i\neq v_i;\forall i\neq j,(u_i,v_i)\neq (u_j,v_j)\)

我当时的思路可谓是经典的错误，标准的零分。把整张图分为一个一个连通块，然后一旦出现可以执行操作\(x\)的三元组，就证明整个连通块都可以执行这个操作直至变成完全图。（然后轻易举出了反例：

\(a\rightarrow b\rightarrow c \rightarrow d;e\rightarrow f\rightarrow g\rightarrow d\)。这样的话\(a\)和\(g\)之间是不会有有向边的。然后就陷入了“嘶，这样的有向边算不算连通块？”“话说这种东西叫连通块吗，我怎么进一步分割？”等等的错误思想中。实际上再从源头进一步想想，就可以知道这个结论：如果在原图中\(x\)可最终抵达\(y\)，那么一定可以添加(或者本来存在)\(x\rightarrow y\)这条边。

本来还在想怎么优化，一抬头看到\(N\times M=4e6\)，乐。E题好简单，我真是猪鼻orz

int n, m;
const int N = 2000 + 10;
vector<int> ve[N];
bool vis[N];
int vertices = 0;

void init(){
    for (int i=1;i<=n;++i){
        vis[i] = false;
    }
    vertices = -1;
}

void dfs(int x){
    vis[x] = true, vertices++;
    int xlen = ve[x].size();
    for (int i : ve[x]){
        if (!vis[i]) dfs(i);
    }
}

int main(void){
    cin >> n >> m;
    int u, v;
    for (int i=1;i<=m;++i){
        cin >> u >> v;
        ve[u].push_back(v);
    }
    ll sm = 0;
    for (int i=1;i<=n;++i){
        init();
        dfs(i);
        sm += vertices;
    }
    cout << sm - m << endl;

    return 0;
}

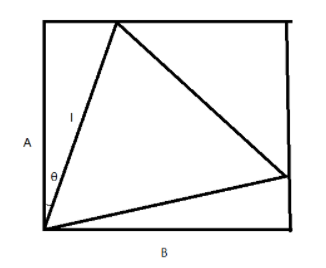
F-Regular Triangle Inside a Rectangle

有一个矩形，边长为正整数\(A,B\)。在矩形里放一个等边三角形，问等边三角形最大的边长是多少。

• 数据范围：\(1\leq A,B \leq 1000;\)

• 数据精度要求：\(10^{-9}\)

• 时间要求：2s

我的小学生数学想法：从长方形的某个顶点出发，印两条夹角为60°的射线，和矩形相交，那么最短的一条交线就是等边三角形的边长。

首先，这个最大的等边三角形，一定会有两个顶点都在矩形边上，不然一定可以找到一个更大的。又大边对大角，小边对小角。\(l_3\)所对的角度是60°，三角形内角和180°，那\(l_1,l_2\)肯定有一条所对的角度小于等于60°，也就是这两条射线的交线中的一条肯定是最小的边长，\(l_3\)不可能是最小的那条边，不需要考虑。

\(l_1=A\times \sec \alpha,l_2=B\times \sec \beta\)

\(\alpha + \beta = 30\)

题目要求精度\(10^{-9}\)，然后\(\cos x\)范围是\([0,1]\)嘛，这就30°，分成1e8还不拿下？嗯……然后1e8刚好超时几十ms，然后5e7就有两个点wa了，经过几次尝试发现8e7过了()

然后看了题解之后发现，啊哈哈，对哦，这题可以二分写，然后写了半天二分没弄懂题目什么意思orz，为什么就检查了一个$\sin\theta\leq A/l,\cos \theta \leq B/l,0\leq \theta \leq 30° $啊，至少不是得检查两条边吗qaq（现在也没搞懂题解一到底在写啥）最后含泪写了三分AC了

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define pi acos(-1.0)
#define ZERO 1e-15

int A, B;
const int M = 8e7;
double d = 30.0 * pi / 180;

int main(void){

    cin >> A >> B;
    if (A > B) swap(A, B);
    double l = 0, r = d, m1, m2, res = -1;
    while (r - l > ZERO){
        double m1 = l + (r - l) / 3;
        double m2 = l + (r - l) / 3 * 2;

        double len1 = min(A / cos(m1), B / cos(d - m1));
        double len2 = min(A / cos(m2), B / cos(d - m2));
        if (len1 > len2){
            r = m2, res = len1;
        }
        else{
            l = m1, res = len2;
        }
    }

    cout << fixed << setprecision(15) << res << endl;

    return 0;
}

看不懂第一个editorial，好烦躁0.0，直接来数学方法：

假设\(A\)为短边，\(B\)为长边，\(\theta\)为\(A\)和三角形边\(l\)的夹角

• 当\(A=B\)，显然\(\theta=15°\)

• 当\(b\)大\(a\)很多时，那么这时等边三角形是被短边限制住的，最大的可以画的三角形就是以短边为高的等边三角形。故\(b\)最小也要是\(\frac{A}{\sin 60°}=\frac{2A}{\sqrt 3}\)

  因此，当\(B\geq \frac{2A}{\sqrt 3}\)时，\(\theta=30°\)

• 当\(A<B<\frac{2A}{\sqrt 3}\)时，\(l = \frac{B}{\cos(30°-\theta)}=\frac{A}{\cos \theta}\)

化简得\(\tan \theta = \frac{2B}{A} - \sqrt 3\)

\(\sec ^2 \theta = 1 + \tan^2 \theta=4 - \frac{4\sqrt 3B}{A} + \frac{4B^2}{A^2}\)

故\(\cos\theta = \frac A {2\sqrt{A^2-\sqrt 3 AB + B^2}}\)

\(l=\frac A {\cos\theta} = 2\sqrt{A^2-\sqrt 3 AB + B^2}\)

代码如下：

int A, B;
double d = pi / 180.0;

int main(void){

    cin >> A >> B;
    if (A > B) swap(A, B);
    double res = -1;
    if (A == B){
        res = A / (cos(15 * d));
    }
    else if (B >= 2.0 * A / sqrt(3)) {
        res = A / (cos(30 * d));
    }
    else{
        res = 2.0 * sqrt(A*A - sqrt(3)*A*B + B*B);
    }

    cout << fixed << setprecision(15) << res << endl;

    return 0;
}