[计算几何] 1 二维基础运算与概念

下面是关于二维计算几何的一些前置知识，不涉及什么算法。在下班回家的时候努力不偷懒的重写了。
计算几何的板子，感觉很容易出错（我下载到的板子也在一些小地方和特殊情况存在问题），所以这些都是我尽量验证过的，但是，也不能保证考虑到了100%的情况，因此推荐在应用之前，也尝试着进行一些验证（比如自己代入特殊点，或者找几个模板题试一下，不推荐在AcWing上测试，数据一般都比较水）

目录

• 常用定理
  • • • 余弦定理
      • 海伦公式
      • 皮克定理
• 常用数据结构定义
  • • 点/向量
    • 直线/线段
      • 数学定义
      • 代码
    • 多边形
    • 圆
• 常用运算
  • • 前置
    • 向量
      • 内积（点积） \(\overrightarrow A·\overrightarrow B = |\overrightarrow A||\overrightarrow B|\cos(\theta)\)
      • 外积（叉积） \(\overrightarrow A\times\overrightarrow B = |\overrightarrow A||\overrightarrow B|\sin(\theta)\)
      • 取模
      • 计算向量夹角
      • 向量\(\overrightarrow A\)顺时针旋转\(\theta\)的角度
      • 计算两点间距离
    • 直线/线段
      • 判断一个线段上有多少个整数点
      • 判断点和直线的关系(点在直线左边/在直线上/在直线右边)
      • 点C是否在线段AB上
      • 点到直线的距离
      • 点\(C\)到线段\(AB\)的距离
      • 点在直线上的投影
      • 两直线的关系
      • 两线段的关系
      • 两直线交点
      • 两线段交点
      • 得到两点的中垂线
      • 极角排序
    • 多边形
      • 判断点与多边形(不一定是凸多边形)的关系
      • 三角形外心, 内心, 垂心, 重心
      • 简单多边形面积（不一定要凸多边形）
    • 圆
      • 三点确定一个圆
      • 计算扇形面积
      • 计算直线和圆的交点和距离
      • 计算圆和三角形的面积交

常用定理

余弦定理

\(c^2=a^2+b^2-2\times a \times b\times \cos (C)\)

海伦公式

\(p=\frac{(a+b+c)}2\)

\(S_{\triangle ABC}=\sqrt{p(p-a)\times (p-b)\times (p-c)}\)

皮克定理

皮克定理指的是一个计算点阵中顶点在格点上的多边形面积公式。该公式可表示为\(S=a+\frac b 2-1\)，其中\(a\)表示多边形内部的点数，\(b\)表示多边形落在格点边界上点数，\(S\)表示多边形的面积。

常用数据结构定义

点/向量，直线/线段，多边形……或者你也可以根据需要再定义一些数据结构。

点/向量

// 向量可以看成一个有向线段, 或者可以想成一个从(0, 0)开始, 指向点P(x, y)的箭头
// 因此, 点的定义可以复用到向量上
struct Point{
    double x, y;
    Point (double _x = 0, double _y = 0) : x(_x), y(_y) {}
    // 重载一些基本符号运算, 也可以重载内积和外积, 或者写在外面
    // -----------------------------------------------
    Point operator + (Point& B) { return Point(x + B.x, y + B.y); }
    Point operator - (Point& B) { return Point(x - B.x, y - B.y); }
    bool operator < (Point& B) {
        if (!sgn(x - B.x)) return y < B.y;
        return x < B.x;
    }
    
    // 喜欢的话还可以加len()和norm()方法
    // -----------------------------
    double len() { return sqrt(x * x + y * y); }
    Point norm() { return Point(x, y) / len(); }
    
    // 重载一些输入输出, 我喜欢重载方便调试
    // ------------------------------
    friend ostream& operator <<(ostream& out, Point& p) { out << "(" << p.x << ", " << p.y << ")"; return out; }
    friend void operator >>(istream& in, Point& p) { in >> p.x >> p.y; }
};
typedef Point Vector;

直线/线段

数学定义

• 一般式：\(ax+by+c=0\)

• 点向式：\(\begin{cases} x=x_0+mt \\ y=y_0+nt \end{cases}\)

  设直线\(L\)过点\(M_0(x_0,y_0)\)，\(\overrightarrow s=\{m,n\}\)是直线\(L\)的向量。设\(M\)为直线\(L\)上任意一点，则\(\overrightarrow {M_0M}=\{x-x_0,y-y_0\}\)，且\(\overrightarrow {M_0M} ~//~~ \overrightarrow s\)。由两向量平行的充要条件可知：

  \(t=\frac{x-x_0}m =\frac{y-y_0}n\)，即直线的点向式方程为：

  \(\frac{x-x_0}m =\frac{y-y_0}n\)（当\(m,n\)中有一个为0时，就理解为相应的分子为0）

• 参数方程：\(\begin{cases} x=x_0+mt \\ y=y_0+nt \end{cases},t\in\R\)

• 斜截式 \(y=kx+b\)

• 两点式 \(\frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1}\)

代码

注意，我后面写的模板，直线有的可能是两点定义，有的可能是点+向量来定义，出现了st, ed的就是两点，出现了p v 的就是点+向量，应该很好区分，如果有需要自己变一下定义方式。

// 直线要么用两个点来定义, 要么用一个点+一个向量来表示
// 我喜欢偷懒用pair
// 有时候还要表示射线, 同理

// 如果用两个点表示, 我会这么定义:
typedef pair<Point, Point> Line;
#define st first
#define ed second

// 如果用点+向量来表示, 我会这么定义:
// typedef pair<Point, Vector> Line;
// #define p first     // 点
// #define v second    // 向量

typedef Line Segment;

多边形

(1) 多边形：由在同一平面且不再同一直线上的多条线段首尾顺次连接且不相交所组成的图形叫多边形

(2) 简单多边形：简单多边形是除相邻边外其它边不相交的多边形

(3) 凸多边形：过多边形的任意一边做一条直线，如果其他各个顶点都在这条直线的同侧，则把这个多边形叫做凸多边形。

• 任意凸多边形外角和均为\(360°\)
• 任意凸多边形内角和为\((n−2)\times 180°\)

// 多边形是由一群点构成的。如果需要，可以把多边形上的按照顺/逆时针的顺序依次存储，我喜欢按照逆时针方向存储
typedef vector<Point> Polygon;

圆

// 圆就是圆心+半径
struct Circle{
    Point oo;
    double r;
    Circle() {}
    Circle(Point _oo, double _r = 0) : oo(_oo), r(_r) {}
};

常用运算

这些运算，理解就好，实际写的时候根据需要会有一点小小的变化。说白了，这些运算大部分都是点积和叉积的运用。

前置

一些杂七杂八的小东西

#define ZERO 1e-8        // 精度, 我就要叫ZERO不叫eps
#define PI acos(-1)      // pi的值, 这样定义精度更高
#define RIGHT -1		 // 如果你觉得有必要, 可以定义left,right,on 这些位置关系
#define ON 0
#define LEFT 1

// 判断x的符号
int sgn(double x){
    if (fabs(x) < ZERO) return 0;
    return x > 0 ? 1 : -1;
}

向量

内积（点积） \(\overrightarrow A·\overrightarrow B = |\overrightarrow A||\overrightarrow B|\cos(\theta)\)

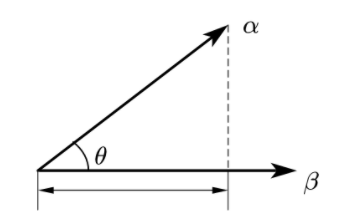
(1) 几何意义：向量\(\overrightarrow A\)在向量\(\overrightarrow B\)上的投影与\(\overrightarrow B\)的长度的乘积。

(2) 公式推导

定义向量\(\overrightarrow c=\overrightarrow a-\overrightarrow b\)

\(c^2=a^2+b^2-2\times |\overrightarrow a||\overrightarrow b|\cos \theta\)

即\((\overrightarrow a -\overrightarrow b)·(\overrightarrow a - \overrightarrow b)=a^2+b^2-2\overrightarrow a·\overrightarrow b=a^2+b^2-2\times |\overrightarrow a||\overrightarrow b|\cos \theta\)

则\(\overrightarrow a ·\overrightarrow b=|\overrightarrow a||\overrightarrow b|\cos \theta\)

(3) 代码实现

// 计算A·B(点积)
double dot(Point A, Point B){
    return A.x * B.x + A.y * B.y;
}

外积（叉积） \(\overrightarrow A\times\overrightarrow B = |\overrightarrow A||\overrightarrow B|\sin(\theta)\)

(1) 几何意义

向量\(\overrightarrow A\)与\(\overrightarrow B\)张成的平行四边形的有向面积。\(\overrightarrow B\)在\(\overrightarrow A\)的逆时针方向为正。

(2) 公式推导

$S= |\alpha|\times|\beta|\times \sin(b-a)= |\alpha|\times |\beta|\times (\sin b\times \cos a-\cos b \times \sin a)\=(|\alpha|\cos a)(|\beta|\sin b)-(|\alpha|\sin a)(|\beta| \cos b)=A.x\times B.y - A.y\times B.x $

(3) 代码实现

// 计算AxB(叉积)
double Cross(Vector A, Vector B){
    return A.x * B.y - A.y * B.x;
}

取模

// 计算|A|
double get_length(Point A){
    return sqrt(dot(A, A));
}

计算向量夹角

\(\theta=\arccos(\frac{\overrightarrow a·\overrightarrow b}{|\overrightarrow a||\overrightarrow b|})\)

// 计算A,B之间夹角, AB可以交换顺序
double get_angle(Point A, Point B){
    return acos(dot(A, B) / get_length(A) / get_length(B));
}

向量\(\overrightarrow A\)顺时针旋转\(\theta\)的角度

\(x_2=OA\times \cos(\alpha -\theta)=OA\times(\cos \alpha \cos \theta+\sin\alpha \sin \theta)=x_1\times \cos \theta+y_1\times \sin \theta\)

\(y_2=OA\times \sin(\alpha -\theta)=OA\times(\sin \alpha \cos \theta-\cos\alpha \sin \theta)=-x_1\times \sin \theta+y_1\times \cos \theta\)

// 向量A顺时针旋转theta度，theta是PI/6之类的, 不是90°,45°这样的
Point Rotate(Point A, double theta){
    return Point(A.x * cos(theta) + A.y * sin(theta), -A.x * sin(theta) + A.y * cos(theta));
}

计算两点间距离

// 这玩意有必要写吗话说
double get_dist(Point p1, Point p2){
    return sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
}

直线/线段

判断一个线段上有多少个整数点

int getPoint(Segment A){
    Vector a = A.ed - A.st;
    return abs(gcd(a.x, a.y)) + 1;
}

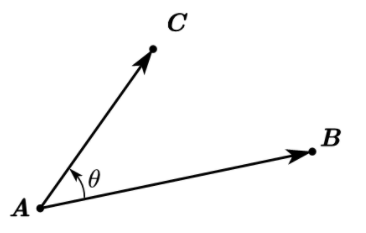
判断点和直线的关系(点在直线左边/在直线上/在直线右边)

判断点\(C\)和直线\(AB\)的关系时，可以转为判断\(x=\overrightarrow {AC}\times \overrightarrow {AB}\)的值。

// 判断直线a和点b的关系
// 1: a在直线左边; 0: a在直线上; -1: a在直线右边 
int relation(Line a, Point b){
    return sgn(cross(a.v, b - a.p));
}

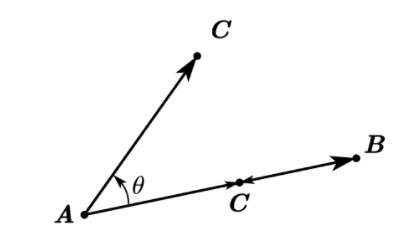
点C是否在线段AB上

首先应满足点\(C\)在直线\(AB\)上，其次满足点\(C\)在线段\(AB\)间。

即：\(\overrightarrow {AC}\times \overrightarrow {AB}=0,\overrightarrow{AC}·\overrightarrow {BC}\leq 0\)。

// 判断点C是否在线段AB上
// 0: 点C不在线段AB上; 1: 点C在线段AB上
bool onSegment(Segment a, Point p){
    return sgn((p - a.st) & (p - a.ed - a.st)) <= 0;
}

点到直线的距离

\(S_{ABCD}=\overrightarrow {v_1}\times \overrightarrow {v_2}=d\times |\overrightarrow {v_2}|\)，\(\therefore d=\frac{\overrightarrow {v_1}\times \overrightarrow {v_2}}{|\overrightarrow {v_1}|}\)

// 返回点C到直线AB的距离
double dis2Line(Point A, Point B, Point C){
    Vector v1 = B - A, v2 = C - A;
    return fabs(Cross(v1, v2) / get_length(v1));
}

点\(C\)到线段\(AB\)的距离

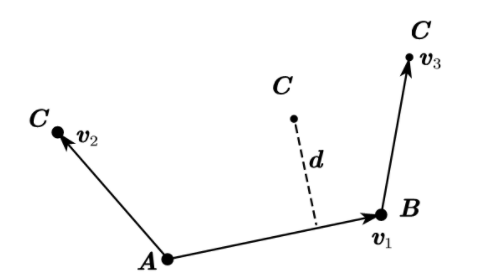
注意：A点必须在B点的左边，否则会计算错误

当\(AB\)为一个点时，返回\(get\_dis(A,C)\)；当\(C\)在线段\(AB\)间时，返回\(dis2Line(C,A,B)\)；

当\(C\)在线段的左边，返回\(|\overrightarrow v_2|\)；当\(C\)在线段的右边，返回\(|\overrightarrow v_1|\)。

// 点C到线段AB的距离, 必须保证A在B点左边或者与B重合
double dis2Segment(Point A, Point B, Point C){
    if (A == B) return get_length(C - A);
    Vector v1 = B - A, v2 = C - A, v3 = C - B;
    if (sgn(dot(v1, v2)) < 0) return get_length(v2);
    if (sgn(dot(v1, v3)) < 0) return get_length(v3);
    return dis2Line(A, B, C);
}

点在直线上的投影

如图点\(D\)的坐标就为\(\overrightarrow {OA} +\overrightarrow {AD}\)，因此，求出\(\overrightarrow {AD}\)即可求出投影点坐标。

\(|\overrightarrow {AD}|=|\overrightarrow {AC}|\times \cos \theta\)，$\overrightarrow {AB}·\overrightarrow {AC}=|\overrightarrow {AC}|\times\cos \theta\times | \overrightarrow {AB}| $

\(\therefore t=\frac{|\overrightarrow {AD}|}{|\overrightarrow {AB}|}=\frac{\overrightarrow {AB}·\overrightarrow {AC}}{|\overrightarrow {AB}|^2}=\frac{\overrightarrow {AB}·\overrightarrow {AC}}{\overrightarrow {AB}·\overrightarrow {AB}}\)

\(\overrightarrow {AD}=\overrightarrow {OA}+\overrightarrow {AB}\times t\)

// 计算点C到直线AB的投影
Point projection2Line(Point A, Point B, Point C){
    Point v = B - A;
    v = v * (dot(v, C - A) / dot(v, v)); // 咳咳, 直接写到一行会报错0.0
    return A + v;
}

两直线的关系

• 相交：\(\overrightarrow A\times \overrightarrow B \neq 0\)

• 平行或共线：\(\overrightarrow A\times \overrightarrow B = 0\)

两线段的关系

具体的原理可以去看快速排斥实验与跨立实验。

二维计算几何基础 - OI Wiki (oi-wiki.org)

// 判断线段A1A2, B1B2是否相交, 这个函数不要求A1A2端点的顺序
bool segmentIntersection(Point a1, Point a2, Point b1, Point b2){
    int c1 = relation(b1, b2, a1), c2 = relation(b1, b2, a2);
    int c3 = relation(a1, a2, b1), c4 = relation(a1, a2, b2);
    if(c1 * c2 < 0 && c3 * c4 < 0) return true;
    return onSegment(b1, b2, a1) || onSegment(b1, b2, a2);
}

两直线交点

// 返回直线a, b的交点
Point getLineIntersection(Line& a, Line& b){
    Vector u = a.p - b.p;
    double t = cross(b.v, u) / cross(a.v, b.v);
    return a.v * t + a.p;
}

两线段交点

// 返回线段a, b的交点
Point getSegmentIntersection(Point a, Vector v, Point b, Vector w){
    if (!sgn(cross(v, w))) return Point(INF, INF);
    Point p = getLineIntersection(a, v, b, w);
    if (onSegment(Segment(a, v), p) && onSegment(Segment(b, w), p)) return p;
    return Point(INF, INF);
}

得到两点的中垂线

// 其实主要是为了用在圆上啦
Line getMidLine(Point& a, Point& b){
    Point m = (a + b) * 0.5;
    Vector v = Rotate(b - a, PI * 0.5);
    return Line(m, v);
}

极角排序

这里其实就是按照直线和x轴正半轴的角度进行从小到大排序，很简单的。如果两条直线平行，那就把更靠左的直线排到前面（本题需要）。

// atan2精度比较高, 要记住它先传入y再传入x
double getAngle(Line& a){
    return atan2(a.ed.y - a.st.y, a.ed.x - a.st.x);
}
bool cmp(Line& x, Line& y){
    double ax = getAngle(x), ay = getAngle(y);
    return (sgn(ax - ay)) ? (ax < ay) : (relation(x, y.ed) < 0);
}

多边形

判断点与多边形(不一定是凸多边形)的关系

• 射线法：从该点任意做一条和所有边都不平行的射线。交点个数为偶数，则在多边形外，为奇数，则在多边形内。

• 转角法

• 判断点在凸多边形内：只需判断点是否在所有边的左边（逆时针存储多边形）

三角形外心, 内心, 垂心, 重心

(1) 外心，外接圆圆心
三边中垂线交点。到三角形三个顶点的距离相等

(2) 内心，内切圆圆心
角平分线交点，到三边距离相等

(3) 垂心
三条垂线交点

(4) 重心
三条中线交点（到三角形三顶点距离的平方和最小的点，三角形内到三边距离之积最大的点）

简单多边形面积（不一定要凸多边形）

// 计算多边形p的面积, p中的点不一定要按照逆时针存储
double area(Polygon& p){
    double res = 0;
    for (int i = 0; i < p.size(); ++i){
        res += cross(p[i], p[(i + 1) % p.size()]);
    }
    return res * 0.5;
}

圆

三点确定一个圆

Circle getCircle(Point& a, Point& b, Point& c){
    Line x = getMidLine(a, b), y = getMidLine(a, c);
    Point oo = getLineIntersection(x, y);
    double r = get_dist(oo, a);

    return Circle(oo, r);
}

计算扇形面积

double getSector(Vector a, Vector b){
    double theta = acos((a & b) / a.len() / b.len());
    if (sgn(cross(a, b)) == -1) theta = -theta;
    return r * r * theta * 0.5;
}

计算直线和圆的交点和距离

// return的r2s是距离, pa, pb是交点
double circleLineIntersection(Line a, Point& pa, Point& pb){
    Point p = getLineIntersection(a, Line(oo, Rotate(a.ed - a.st, PI * 0.5)));
    double r2s = get_dist(oo, p);
    if (!onSegment(a, p)){
        r2s = min(get_dist(oo, a.st), get_dist(oo, a.ed));
    }
    if (sgn(r - r2s) <= 0) return r2s; // segment and circle have not intersection
    double len = sqrt(r * r - get_dist(oo, p) * get_dist(oo, p));
    pa = p + (a.st - a.ed).norm() * len;
    pb = p + (a.ed - a.st).norm() * len;
    return r2s;
}

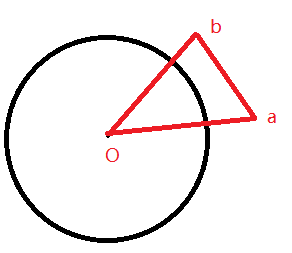
计算圆和三角形的面积交

这里的三角形特指三个顶点分别为圆心，a和b的三角形，如下图：

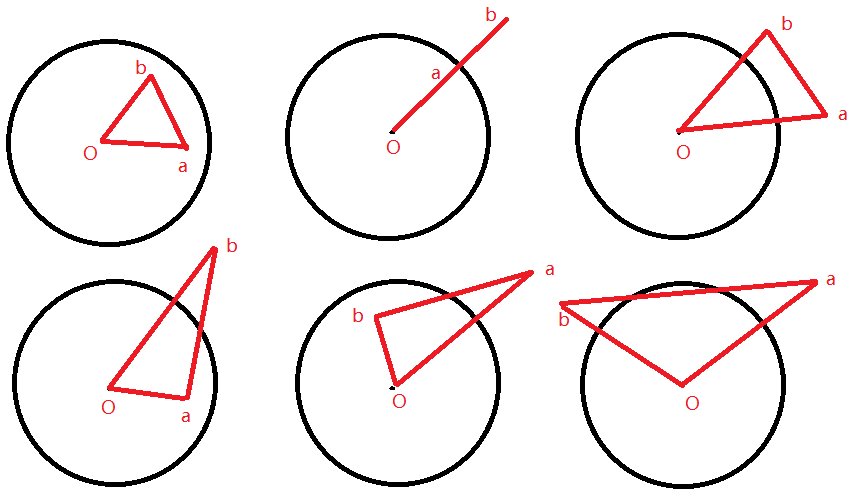
// 这里分情况讨论还是挺烦的, return面积交
double circleTriangleIntersection(Point a, Point b){
    double ra = get_dist(oo, a), rb = get_dist(oo, b);
    // a,b in the circle
    if (sgn(r - ra) >= 0 && sgn(r - rb) >= 0) return cross(a, b) * 0.5;
    // a, b, r on the same line
    if (!sgn(cross(a, b))) return 0;
    Point pa, pb;
    double r2s = circleLineIntersection(Line(a, b), pa, pb);
    // segment and circle have not intersection
    if (sgn(r - r2s) <= 0) return getSector(a, b);
    // a in the circle, b outside the circle
    if (sgn(r - ra) >= 0) return cross(a, pb) * 0.5 + getSector(pb, b);
    // b in the circle, a outside the circle
    if (sgn(r - rb) >= 0) return cross(pa, b) * 0.5 + getSector(a, pa);
    // a,b outside the circle, segment and circle have 2 intersection points
    return getSector(a, pa) + cross(pa, pb) * 0.5 + getSector(pb, b);
}

碎碎念：一定要验证啊，千万不要发生拿着枪上战场然后发现手里的是拿的是巴拉拉魔仙棒啊（