简单回归模型

逻辑回归

逻辑回归模型主要用于二分类，即预测样本是正样本还是负样本。 二分类问题一般默认类别标签为0和1，只需判断是不是1类就可以了，因为不是1类则是0类。

模型

我们假设模型是：

\[\hat y=\mathbf {xw}+b,\mathbf x\in \mathbb{R}^{1\times m},\mathbf w\in\mathbb{R}^{m\times 1} \]

我们得到的是一个数值，而我们期望得到预测标签 \(1\) 的概率。在数学里通常用函数 \(\text{sigmoid}(x)=\frac{1}{1 + e^{-x}}\) 将数值转化为概率。

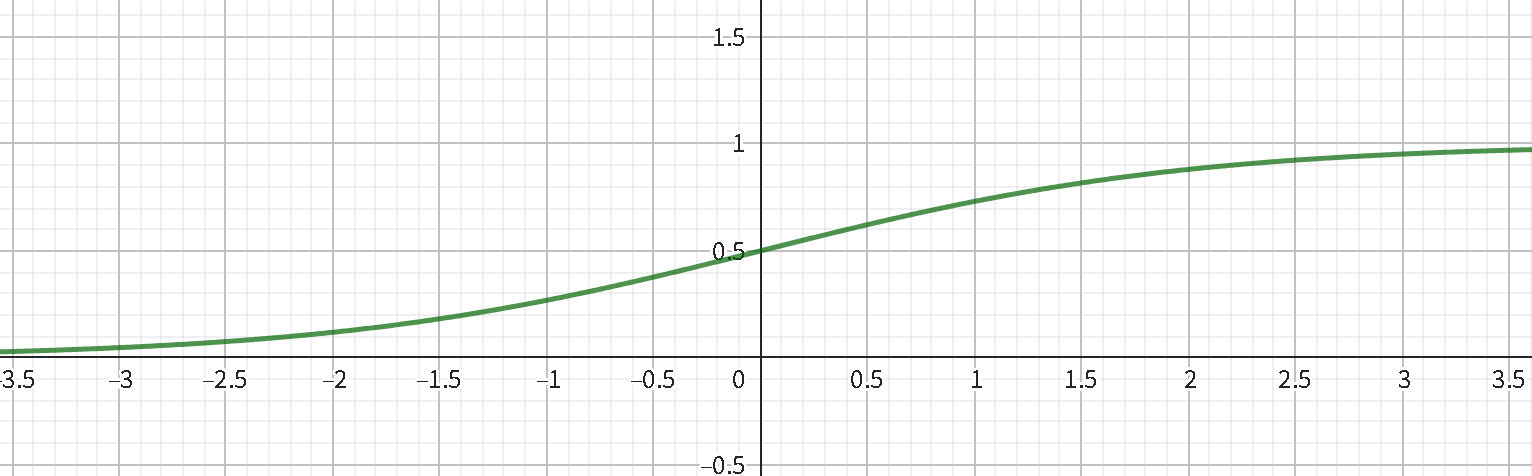
最终逻辑回归公式(模型表达式)如下：

\[\hat y=\text{Sigmoid}(\mathbf{xw}+b)=\frac{1}{1 + e^{-(w_1x_1 + w_2x_2+\cdots+w_kx_k + b)}} \]

损失函数

我们利用极大似然估计去推导出该模型的损失函数。

对于单个样本，预测准确的概率是：

\[P(y=1|\mathbf{w},b)=\hat{y},P(y=0|\mathbf{w},b)=1-\hat{y} \]

那么联合概率就是：

\[P(y|\mathbf{w},b)=\hat y^y (1-\hat y)^{1-y} \]

即对于 \(n\) 个样本输入，我们要最大化：

\[P(\mathbf y|\mathbf{w},b)=\prod_{i=1}^n P(y_i|\mathbf{w},b)=\prod_{i=1}^n \hat y_i^{y_i} (1-\hat y_i)^{1-y_i} \]

所以只需将损失函数设计为 \(-P(\mathbf y|\mathbf{w},b)\)，由于有大量乘积，结果容易过大，所以取个对数。（损失函数是要求最小化）

\[l(\mathbf y,\mathbf{ \hat y})=-\log P(\mathbf y|\mathbf{w},b)=-\sum_{i=1}^n y_i\log \hat y_i+(1-y_i)\log (1-\hat y_i) \]

梯度下降训练

对损失函数关于 \(\mathbf w\) 求导得到：

\[\frac{\partial l(\mathbf w)}{\partial \mathbf w} = \mathbf X^T(\mathbf{\hat y}-\mathbf y) \]

关于 \(b\) 求导得到：

\[\frac{\partial l(b)}{\partial b} = \mathbf{\hat y}-\mathbf y \]

设初始参数为 \(\mathbf w_0,b_0\)，正在进行第 \(n\) 次迭代训练，那么有：

\[\mathbf w_n=\mathbf w_{n-1} - \eta\frac{\partial l(\mathbf w)}{\partial \mathbf w} \]

\[b_n=b_{n-1}-\eta \frac{\partial l(b)}{\partial b} \]

其中 \(\eta\) 是学习率。

softmax回归

逻辑回归只能解决二分类问题，但我们一般需要解决的是多分类问题。

独热编码（one-hot encoding）是一个向量，大小等于类别数，如 \((1,0,0),(0,1,0,0)\)。其中 \(1\) 代表属于这个类别， \(0\) 则代表不属于。

模型

设有 \(d\) 个特征，\(m\) 个标签，我们构建模型：

\[\mathbf{\hat y}=\mathbf {xW}+\mathbf b,\mathbf x\in \mathbb{R}^{1\times d},\mathbf W\in \mathbb{R}^{d\times m},\mathbf b\in \mathbb{R}^{1\times m} \]

我们希望得到每一个类别的期望概率，但容易发现 \(\mathbf{\hat y}\) 的分量总和不为 \(1\)，所以我们需要校准概率。

现在重新假设模型为：

\[\mathbf{o}=\mathbf {xW}+\mathbf b,\mathbf x\in \mathbb{R}^{1\times m},\mathbf W\in \mathbb{R}^{m\times m},\mathbf b\in \mathbb{R}^{m\times 1} \]

那么引入 \(\rm{softmax}\) 函数：

\[\mathbf{\hat y}=\mathrm {softmax}(\mathbf o),y_i=\frac{\exp(o_i)}{\sum_k\exp(o_k)} \]

这里，对于所有的 \(j\)总有 \(0 \le \hat y_j \le 1\)。因此，\(\hat y\) 可以视为一个正确的概率分布。softmax运算不会改变未规范化

的预测 \(\mathbf o\) 之间的大小次序，只会确定分配给每个类别的概率。因此，在预测过程中，我们仍然以出现的最大概率判断最有可能的类别。

损失函数

容易求出联合概率：

\[P(\mathbf{y^{(i)}}|\mathbf{W},\mathbf{b})=\prod_{j=1}^m P(y^{(i)}_j|\mathbf{W},\mathbf{b})=\prod_{j=1}^m (\hat y^{(i)}_j)^{y^{(i)}_j} \]

对于 \(n\) 个样本来说，即：

\[P(\mathbf {Y|W},\mathbf b)= \prod_{i=1}^n P(\mathbf{y^{(i)}}|\mathbf{W},\mathbf{b})=\prod_{i=1}^n\prod_{j=1}^m (\hat y^{(i)}_j)^{y^{(i)}_j} \]

根据极大似然估计，我们最大化 \(P(\mathbf {Y|W},\mathbf b)\)，相当于最小化负对数似然：

\[-\log P(\mathbf {Y|W},\mathbf b)=-\sum_{i=1}^n\sum_{j=1}^m y^{(i)}_j \log \hat y^{(i)}_j \]

所以我们得到了损失函数：

\[l(\mathbf Y,\mathbf {\hat Y})=-\sum_{i=1}^n\sum_{j=1}^m y^{(i)}_j \log \hat y^{(i)}_j \]

这个损失函数其实就是交叉熵，可以参照信息论。

梯度下降训练

对损失函数关于 \(\mathbf W\) 求导得到：

\[\frac{\partial l(\mathbf W)}{\partial \mathbf W} = \mathbf X^T(\mathbf{\hat Y}-\mathbf Y) \]

关于 \(b\) 求导得到：

\[\frac{\partial l(b)}{\partial b} = \sum_{i=1}^n\mathbf{\hat y^{(i)}}-\mathbf y^{(i)} \]

设初始参数为 \(\mathbf W_0,b_0\)，正在进行第 \(n\) 次迭代训练，那么有：

\[\mathbf W_n=\mathbf W_{n-1} - \eta\frac{\partial l(\mathbf W)}{\partial \mathbf W} \]

\[b_n=b_{n-1}-\eta \frac{\partial l(b)}{\partial b} \]

其中 \(\eta\) 是学习率。