线性回归：梯度下降法原理与实现

目录

• 一、线性回归
• 二、梯度下降法的数学原理
• 三、梯度下降法优化
• 四、Python实现

一、线性回归

  关于线性回归的详细介绍可以参见我的上一篇博文《线性回归：最小二乘法实现》。在《线性回归：最小二乘法实现》中我已经说明了线性回归模型建立的关键在于求解：

\[(w^*, b^*)=\arg\min\sum^{m}_{i=1}{{(f(x_i)-y_i)^2}} \]

  这里再介绍另一种求解算法：梯度下降法。

二、梯度下降法的数学原理

  假设有以下问题：

\[w=\arg\min f(w) \]

  通过泰勒一阶展开则有：

\[f(w)=f(w_0)+(w-w_0)∇f(w_0) \]

  图示如下：

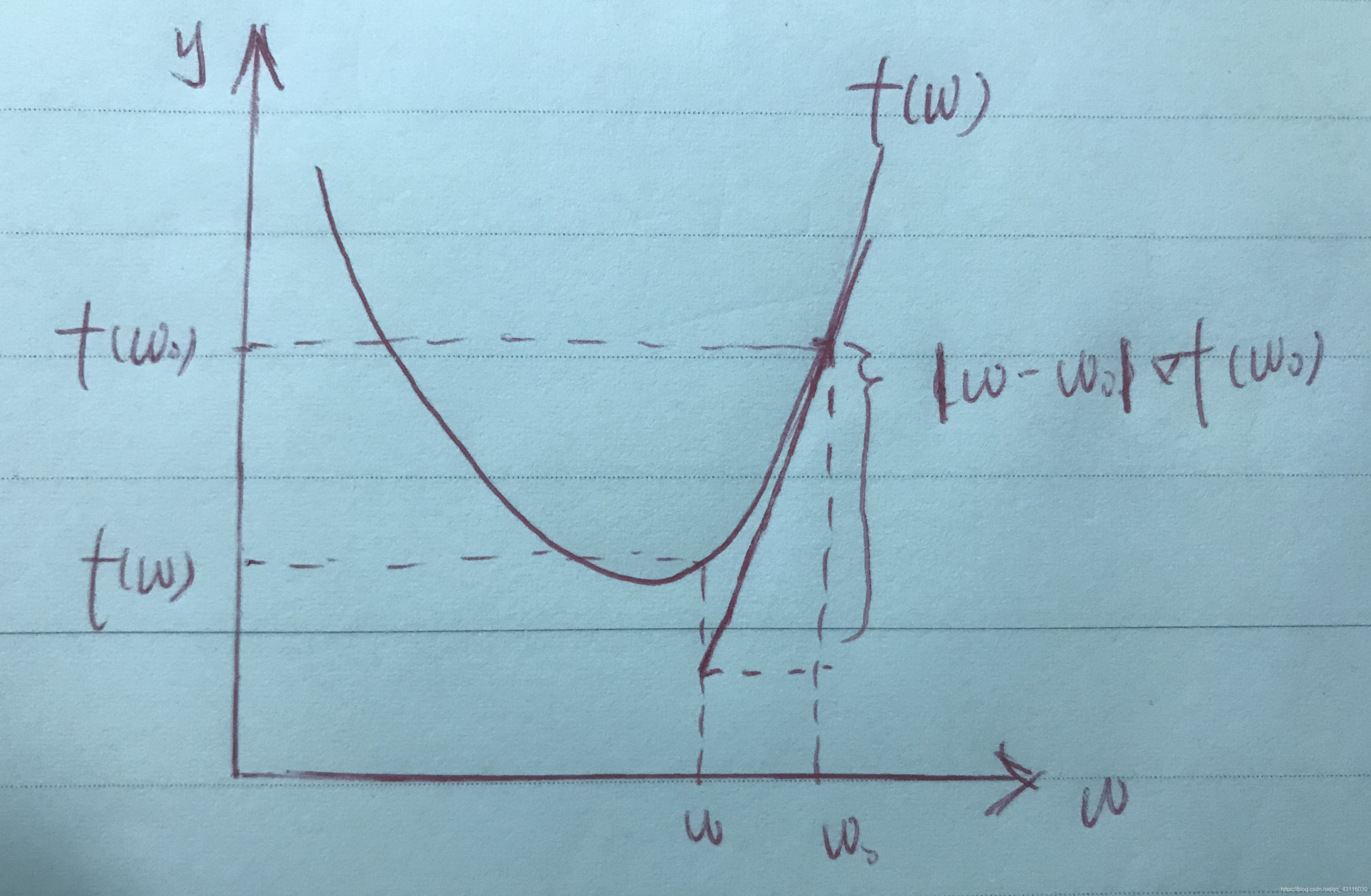
  这里的\(w-w_0\)表示了移动的步长和方向，那么可以有\(w-w_0=\eta\gamma\)，\(\eta\)为实数，表示移动的步长，\(\gamma\)为一个单位向量，表示步长移动的方向。\(f(w_0)+(w-w_0)∇f(w_0)\)则是\(f(w)\)在\(w\)处的邻近估计，此处要求\(\eta\)较小，否则将导致估计的精确度降低。
  梯度下降算法的目的是让优化函数\(f(w)\)尽快到达全局最小值，所以便有了第一个条件：

\[condition1:f(w)-f(w_0)=\eta\gamma∇f(w_0)≤0 \]

  由于\(\eta\)是一个大于0的常数，所以可以暂不考虑。那么就需要满足\(\eta\gamma∇f(w_0)≤0\)并且尽可能小。又有：

\[\gamma∇f(w_0)=|\gamma||∇f(w_0)|\cos \alpha \]

所以想要使\(\eta\gamma∇f(w_0)≤0\)并且尽可能小则需要满足条件：

\[condition2:\cos \alpha=-1 \]

  换句话说，也就是要求单位向量\(\gamma\)和\(∇f(w_0)\)方向完全相反，所以便可以得到以下结论：

\[condition3:\gamma=\frac{-∇f(w_0)}{|∇f(w_0)|} \]

  将\(condition3\)带入\(w-w_0=\eta\gamma\)，则有：

\[condition4:w-w_0=\eta\frac{-∇f(w_0)}{|∇f(w_0)|} \]

  由于\(\eta\)和\(|∇f(w_0)|\)都是大于0的实数，所以可以合并为新的\(\eta^*=\frac{\eta}{|∇f(w_0)|}\)，再对等式进行移项便可以得到：

\[condition5:w=w_0-\eta∇f(w_0) \]

  \(condition5\)便是梯度下降算法中\(f(w)\)的参数\(w\)的更新公式。同时这也解释了为什么需要以梯度的反方向来更新权重。

三、梯度下降法优化

  下面就用梯度下降算法来对线性回归模型进行优化。这里将线性回归模型的代价函数E写为如下形式（方便运算）：

\[E=\frac{1}{2m}\sum^{m}_{i=1}{(f(x_i)-y_i)^2} \]

对其求导：

\[\frac{\partial E}{\partial w}=\frac{1}{m}\sum^{m}_{i=1}{(wx_i-y_i)\frac{\partial (wx_i-y_i)}{\partial w}}=\frac{1}{m}\sum^{m}_{i=1}{(wx_i-y_i)x_i} \]

  由前面的\(condition5\)可以得到权重的更新公式：\(w^*=w+\Delta w\)，此处的\(\Delta w=-\eta∇f(w_0)\)。所以最终可以得到权重的更新公式为：

\[w^*=w+\frac{\eta}{m}\sum^{m}_{i=1}{(y_i-wx_i)x_i} \]

四、Python实现

  由之前推导出的更新公式可以实现出以下拟合算法：

def _gradient_descent(self, X, y):
	for i in range(max_iter):
		delta = y - self._linear_func(X)
		self.W[0] += self.eta * sum(delta) / X.shape[0] # 第一列全部为1
		self.W[1:] += self.eta * (delta @ X) / X.shape[0]

  导入波士顿数据集进行测试：

if __name__ == "__main__":
    from sklearn import datasets
    from sklearn.model_selection import train_test_split
    from sklearn.preprocessing import MinMaxScaler
    boston = datasets.load_boston()
    X = boston.data
    y = boston.target
    scaler = MinMaxScaler().fit(X)
    X = scaler.transform(X)
    X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, test_size=0.3)
    lr = LinearRegression().fit(X_train, y_train)
    y_pred = lr.predict(X_test)
    from sklearn.metrics import mean_squared_error
    print(mean_squared_error(y_test, y_pred))
    plt.figure()
    plt.plot(range(len(y_test)), y_test)
    plt.plot(range(len(y_pred)), y_pred)
    plt.legend(["test", "pred"])
    plt.show()

均方误差：

代价曲线：

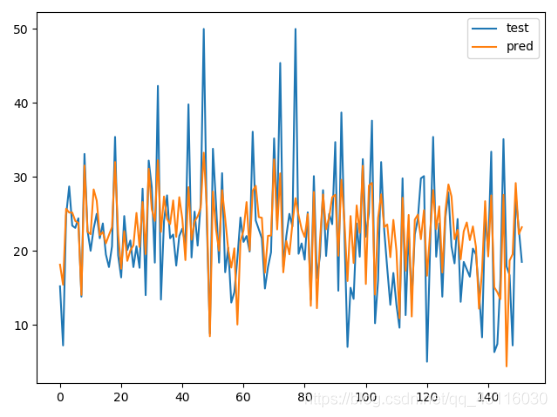
拟合曲线：