离群值 Outliers

目录

• 标准化
• 标准化中的离群值
  • 移除离群值
    • 使用标准差的方法
    • 使用四分位距的方法

标准化

\[\begin{align*} \pmb x&=\left(x^{(1)},x^{(2)},\dots,x^{(n)}\right)\\ \pmb\mu&=\frac1m\sum_{i=1}^m\pmb x_i\\ \pmb\sigma&=\sqrt{\delta+\frac1m\sum_{i=1}^m(\pmb x_i-\pmb\mu)^2}\\ \pmb x'&={\pmb x-\pmb\mu\over\pmb\sigma} \end{align*} \]

其中 \(\delta\) 为一个很小的正值。

标准化中的离群值

离群值对标准化的计算会有很大影响。

离群值是数据中那些远离主流数据的样本。可能由以下几个原因产生：

• 测量错误或输入错误；
• 数据损坏；
• 确实观察到了离群值。

但在大多数情况下，没有特定的检测离群值的手段。

移除离群值

使用标准差的方法

对于高斯分布的数据，标准差表明了数据分布的百分比：1 个标准差 68%；2 个标准差 96%；3 个标准差 99.7%。

如果选择 2 个标准差作为离群值阈值，则会去掉样本中所有差值大于 2 个标准差的样本。从分布上来看，去除了 4% 的离群值。

def standard_deviation(array: np.ndarray):
    mean = array.sum() / array.size
    std = ((array ** 2).sum() / array.size) ** 0.5
    lower_bound, upper_bound = mean - std * 2, mean + std * 2
    return array[(lower_bound < array) & (upper_bound > array)]

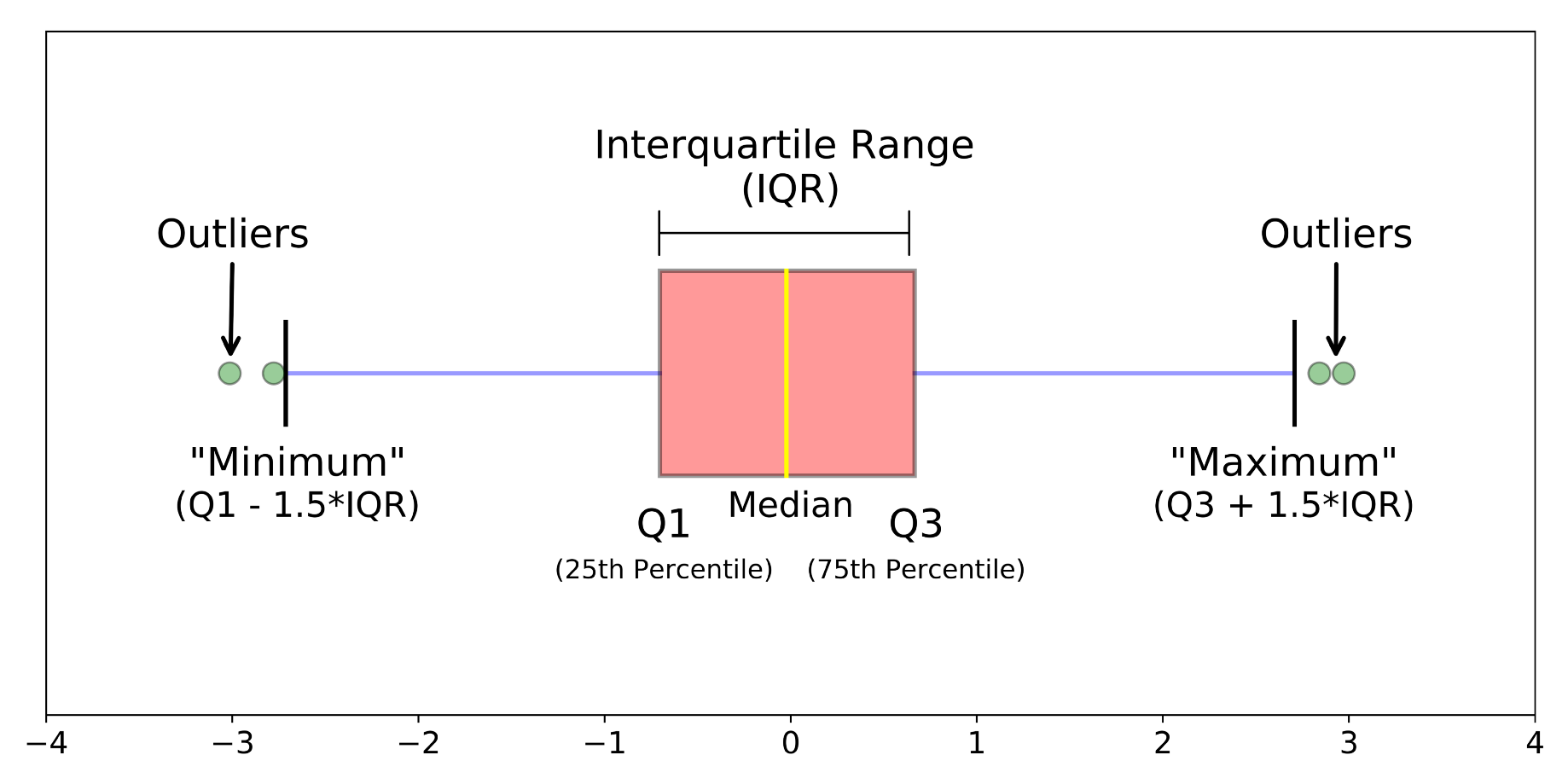
使用四分位距的方法

这一方法对应箱形图（box plot），将四分位点的 1.5 倍范围以外判定为离群值，当然也可以使用其他比例，但 1.5 比较常用。

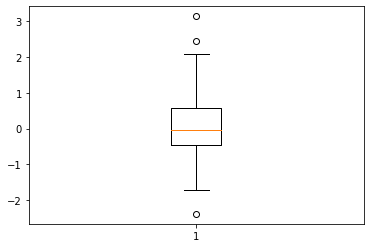
np.random.randn() 使用高斯分布，画出对应的箱形图为

x = np.random.randn(100)
plt.boxplot(x)
plt.show()

def interquartile_range(array: np.ndarray):
    p25, p75 = np.percentile(array, 25), np.percentile(array, 75)
    bound = (p75 - p25) * 1.5
    lower_bound, upper_bound = p25 - bound, p75 - bound
    return array[(lower_bound < array) & (upper_bound > array)]

相对应的，有一种变换方法比起标准化更能应对离群值，其方法为将数据减去中位数后缩小上下四分位点之差。

(x - np.median(x)) / (np.percentile(x, 75) - np.percentile(x, 25)