乘法器原理与硬件实现

乘法运算

乘法运算在数字信号处理中被广泛应用，如滤波器以及各种变换等。这里讨论乘法器的各种设计方法。尽管Verilog语言中有关键字signed（没有unsingned)，借助其可方便地用"\(*\)"描述无符号数乘法和有符号乘法，但同样可根据目标需求（速度优先还是资源优先）采用其他方式实现乘法运算，以达到系统的最佳配置。

1. 二进制乘法原理

二进制乘法原理与十进制乘法原理类似，都是将乘数的每一位分别与被乘数相乘，除此之外，二进制乘法还有其自身的特点，这对于硬件设计极为关键。

二进制乘法可分为两种情况：无符号数乘法和有符号数乘法。无符号数相乘较为简单，如图1.1所示为两个无符号数(3)和(6)相乘。这里，将它们分别用3bits二进制表示为(011)和(110)，相乘结果为(18)，以二进制表示为(10010)。从图1.1中可以看出，整个相乘过程可分解为一系列的移位、相加操作。

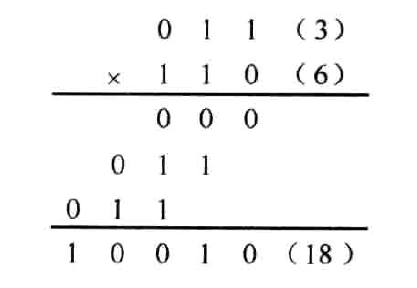
图1.1 两个无符号数相乘

对有符号数乘法，可分为以下四种情况：
（1）正数 x 正数；（2）正数 x 负数；（3）负数 x 正数；（4）负数 x 负数。

1.1 正数 x 正数

以(3)x(6)为例，其中，\((3)_{10}=(0011)_{2C}\)（3以4bits二进制补码表示），\((6)_{10}=(0110)_{2C}\)。运算过程如图1.2所示。

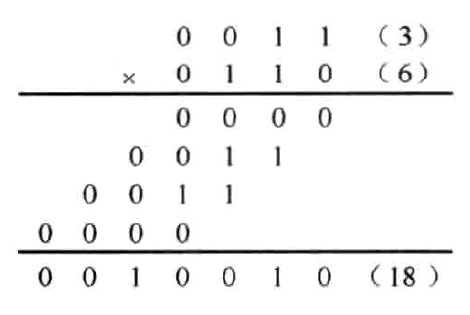
图1.2 两个正数相乘

1.2 正数 x 负数

以(3) x (-6)为例，其中\((3)_{10}=(0011)_{2C},(-6)_{10}=(1010)_{2C}\)。为了保证结果的正确，首先要将两个数进行符号位扩展，扩展为8bits。运算过程如图1.3所示。运算结果取低8位。-18以二进制补码表示时至少需要6bits。这样，-18的6bits二进制补码为(101110)，可见结果是正确的，可认为将(101110)进行符号位扩展得(11101110)。

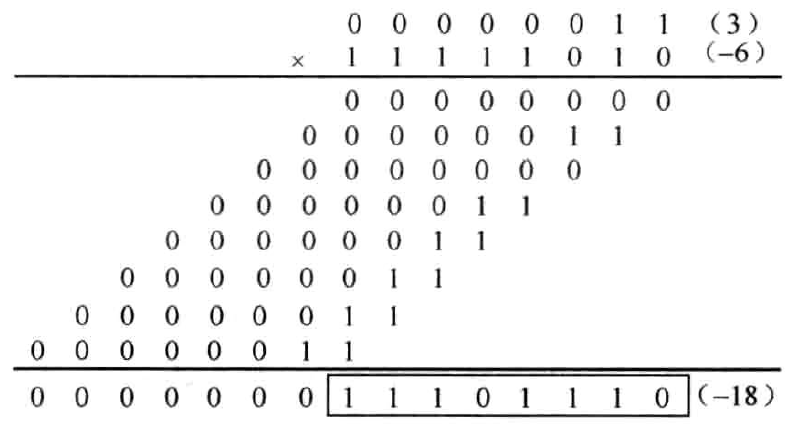
图1.3 正数与负数相乘

1.3 负数 x 正数

以(-3)x(6)为例，其中\((-3)_{10}=(1101)_{2C},(6)_{10}=(0110)_{2C}\)。为了保证结果的正确，首先要将两个数进行符号位扩展，扩展为8bits。运算过程如图1.4所示。运算结果取低8位。不难验证结果的正确性。

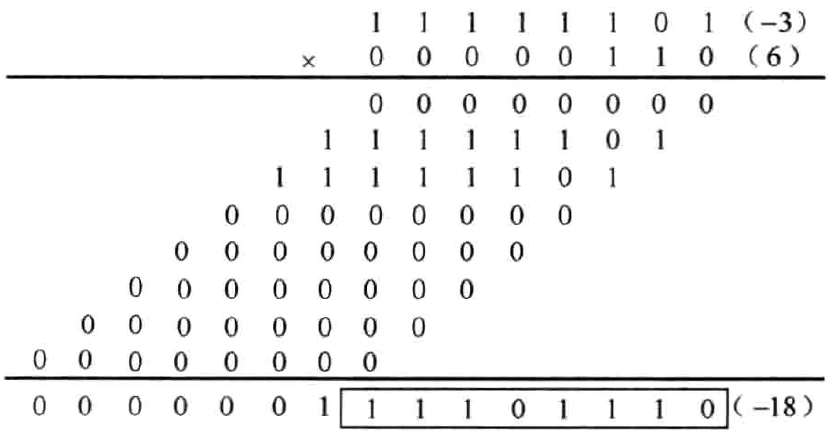
图1.4 负数与正数相乘

1.4 负数 x 负数

以(-3)x(-6)为例，其中\((-3)_{10}=(1101)_{2C},(-6)_{10}=(1010)_{2C}\)。为了保证结果的正确，首先要将两个数进行符号位扩展，扩展为8bits。运算过程如图1.5所示。运算结果取低8位。

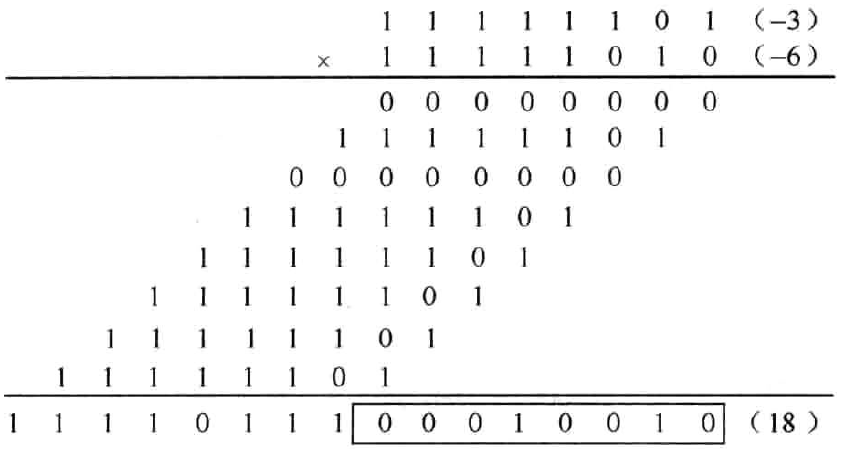
图1.5 负数与负数相乘

假定被乘数和乘数位宽为\(M_{1}\)和\(M_{2}\)，根据以上分析可得如下结论：
（1）无论是无符号数相乘还是有符号数相乘，其乘积位宽必定为\(M_{1}+M_{2}\);
（2）如果被乘数和乘数均为有符号数，那么相乘之前要进行符号位扩展，将被乘数和乘数均扩展为\(M_{1}+M_{2}\)位。

2. 基于移位相加的乘法器

根据上面乘法运算的过程可以发现：乘法运算最终可分解为一系列的移位、相加操作。这就是移位相加型乘法器的设计依据。

以两个无符号数(3)，(6)相乘分析说明。\((6)_{10}=(110)_{2}\)，设定 \(b_{2}=1,b_{1}=1,b_{0}=0\)，分别表示了(6)的二进制补码的第2位，第1位和第0位，则(3)x(6)可表示为：

\[ \begin{aligned} 3\times 6 &= 3\times(1\times 2^2+1\times 2^1 + 0\times 2^0) \\ &= 3\times 2^2 + 3\times 2^1 \end{aligned} \tag{2.1} \]

\(3\times 2^2\)表示将3左移两位，\(3\times 2^1\)表示将3左移一位，由此可得如图2.1所示的硬件结构。从图中可以看出\(b_{i}(i=0,1,2)\)在乘法运算过程中发挥的作用，它将决定MUX的输出是0还是移位后的结果。首先要对被乘数和乘数高位补零，使补零后的位宽为6bits。图中SL(Shift Left)为左移操作，将输入数据左移一位。三个MUX控制端分别为\(b_{0},b_{1},b_{2}\)相连。当控制端为1时，MUX输出移位后的结果，否则输出全零。移位的结果相加为最终乘积。

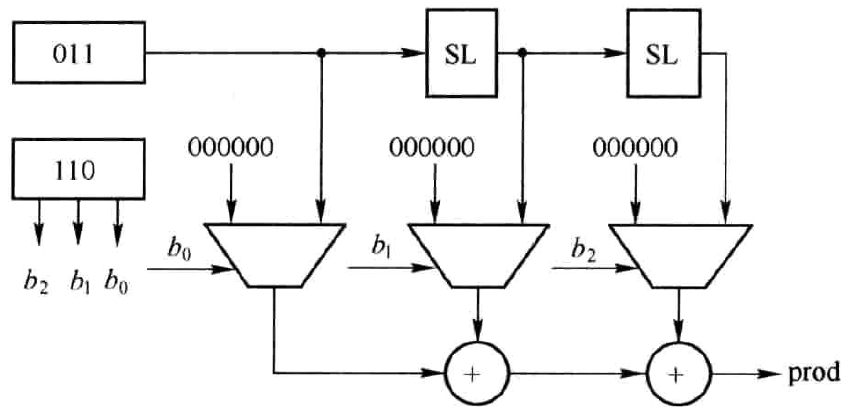
图2.1 移位相加型无符号数乘法器硬件结构

从另一角度看，图2.1中SL和加法器可分时复用，那么就形成了如图2.2所示的硬件结构。图中依然有左移操作模块SL和数据选择器MUX，此外增加了右移操作模块SR和位选择模块BG（Bit Get)。SR模块的目的是将另一输入数据逐步右移以获取\(b_{0},b_{1},b_{2}\)。BG模块则是选择右移结果的最低位输出作为MUX的控制端。nd为ain和bin更新标记信号，高有效。这个结构存在的问题是有组合逻辑反馈支路，所以，最好在SL和SR输出端添加寄存器，这样的nd的周期将变为4个时钟周期。

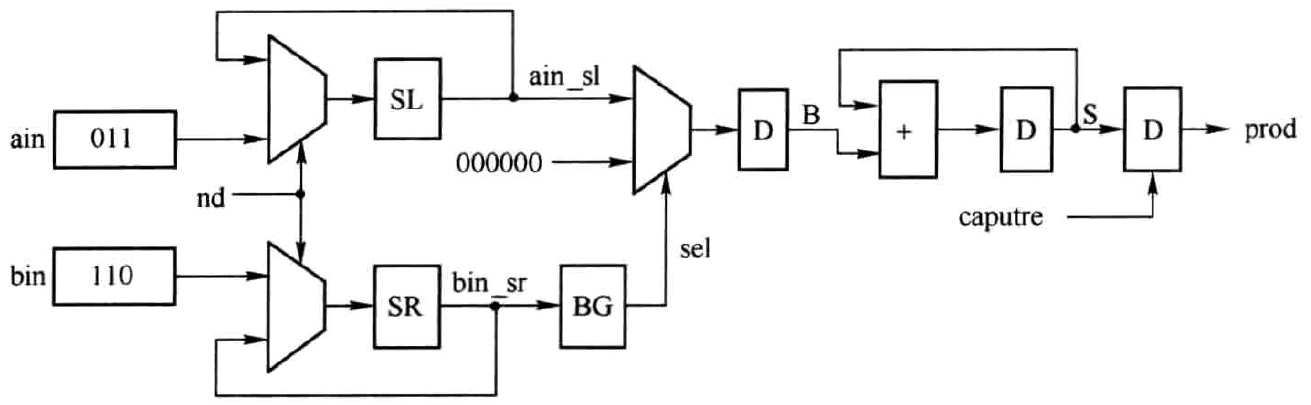
图2.2 移位相加型无符号数乘法器分时复用硬件结构

与图2.2相应的时序如图2.3所示。图中nd(new data)为新输入数据标志信号，高有效。ain,bin为输入数据，其中需要对ain进行高位补零，使最终位宽与乘积位宽一致。该时序显示了(3)x(6)与(5)x(5)的求积过程。ain左移得到ain_sl,bin右移得到bin_sr，而sel则是bin_sr的最低位。当sel为1时，节点B输出ain_sl，否则输出0。节点S显示了累加的过程。捕获信号capture为高时将乘积结果输出至prod端。

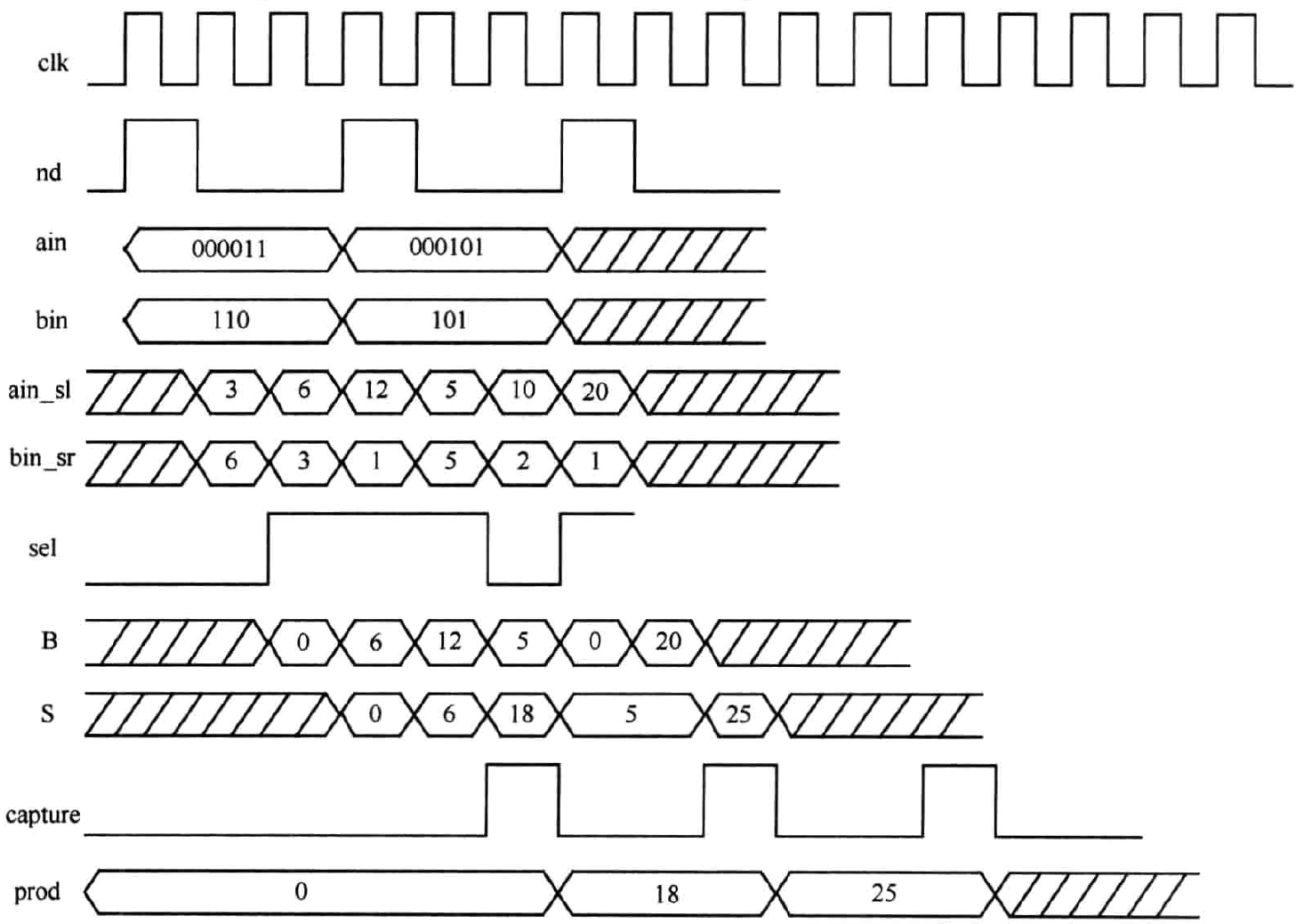
图2.3 移位相加型无符号数乘法器分时复用结构的时序图

从时序图中可以看出，从输入到输出的Latency与输入数据的位宽有关，这意味着输入数据以慢速率进行，而内部运算则是以快速率进行。以\(f_{in}\)表示输入数据速率，以\(f_{clk}\)表示内部运算速率，以\(W_{din}\)表示输入数据位宽，则它们之间的关系可表示为：

\[f_{clk} = W_{din}f_{in} \tag{2.2} \]

而这也正反映了nd与capture周期的来历，二者周期均取决于输入数据的位宽。显然这是一种串行结构，使得输入数据速率与内部运算速率无法达到一致。为此，可采用全并行的结构，如图2.4所示。图中SLi(i=0,1,2)表示对输入数据ain左移i位。BGi(i=0,1,2)表示获取输入数据bin的第i位。整个结构式一个全流水结构，输入数据速率可以和内部运算速率完全一致，但付出的代价是资源的增加。

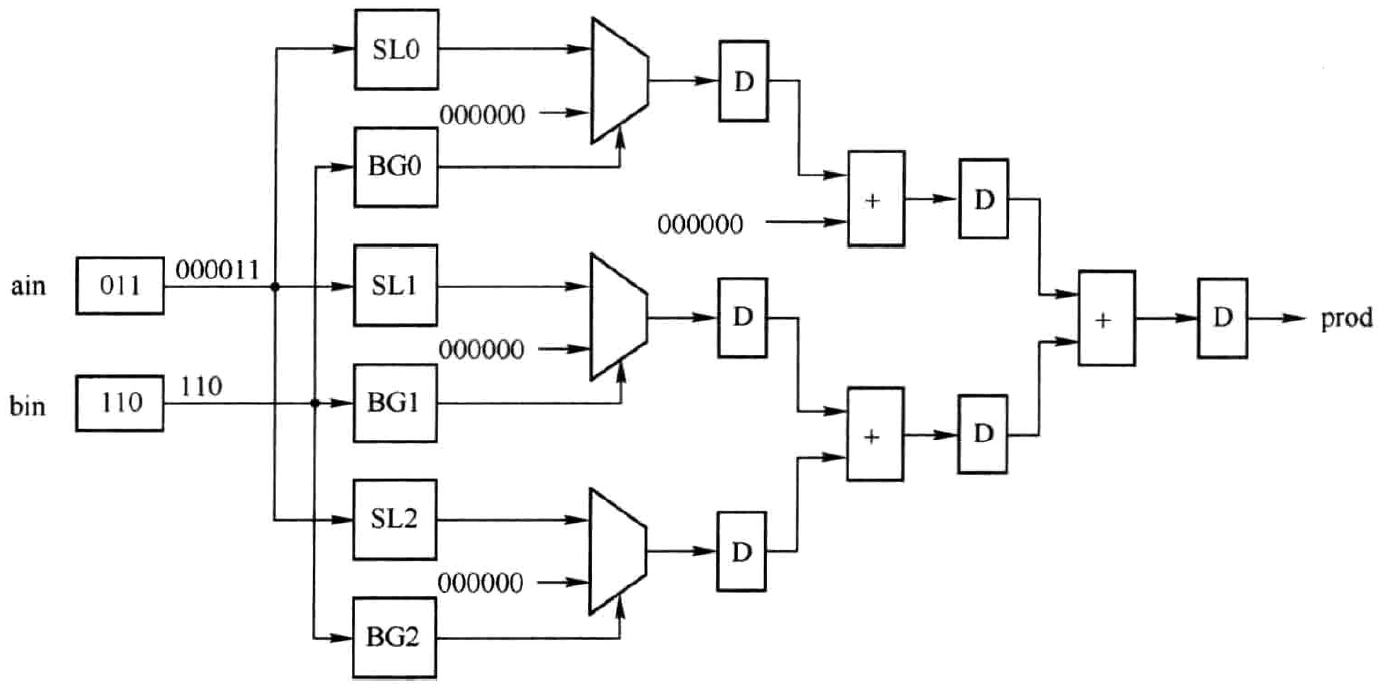
图2.4 全并行移位相加型乘法器硬件结构

对于有符号数的相乘仍然可以采用上述结构，以(-3)x(6)为例。(-3)以4位二进制补码表示为(1101)，(6)以4位二进制补码表示为(0110)，则

\[\begin{aligned} -3\times 6 &= (-1\times 2^3 + 1\times 2^2 + 0\times 2^1 + 1\times 2^0)\times 6 \\ &= -2^3\times 6 + 2^2 \times 6 + 2^0 \times 6 \end{aligned} \tag{2.3} \]

故可得如图2.5所示的硬件结构。与图2.6相比，首先需要对输入数据ain符号位扩展为8bits；其次，bin的最高位除了作为MUX的控制端外，还用作相应的加法器的控制端，当其为1时，加法器执行减法操作，否则执行加法操作，这在式\((2.3)\)有所体现。

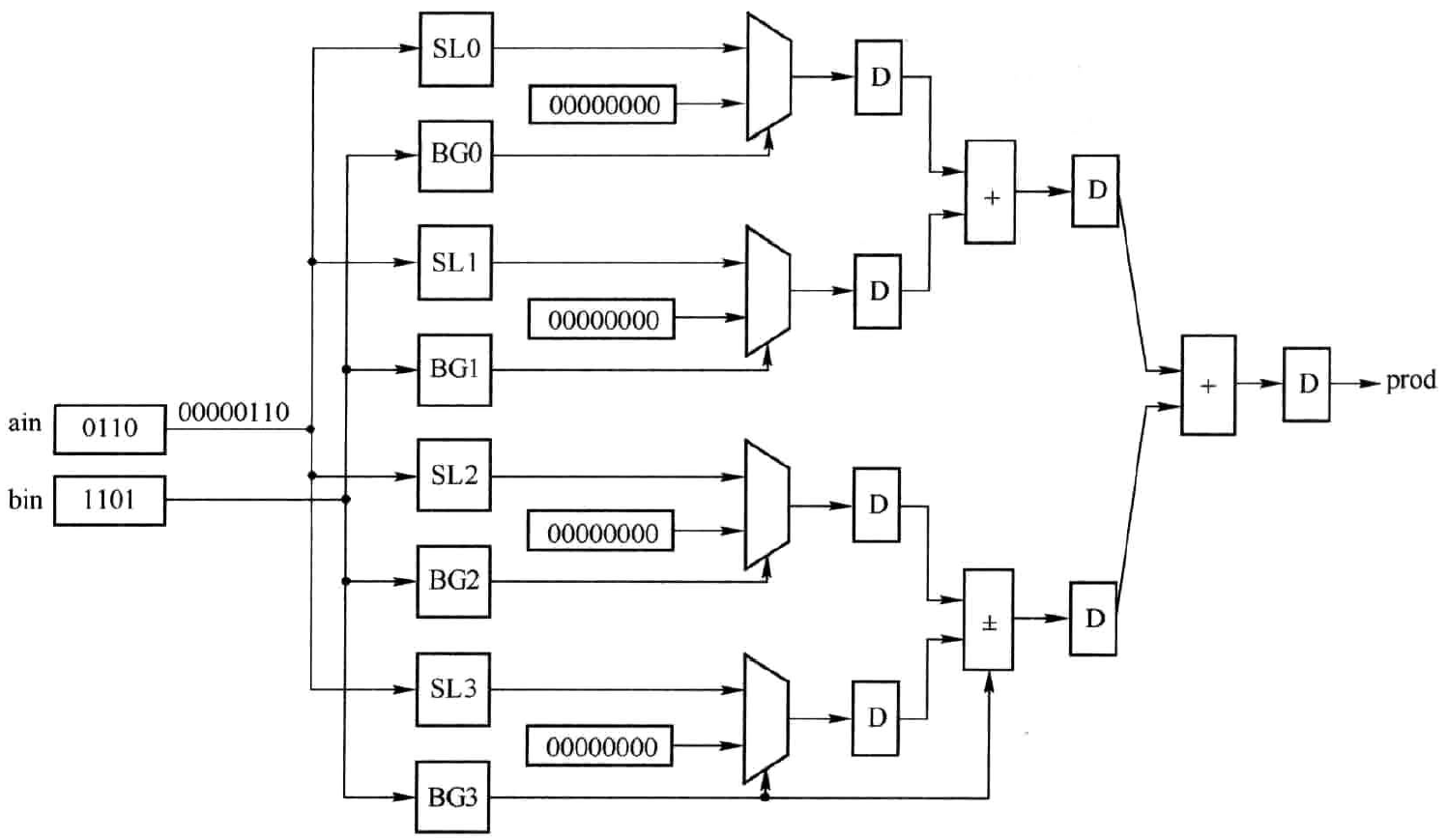
图2.5 移位相加型有符号数乘法器硬件结构

3. 基于ROM的乘法器

乘法器的另一种实现思想是采用ROM的方式，即将被乘数与乘数连接起来拼成地址，把两者所有可能的乘积按照地址号存在放ROM的地址空间内，两个数相乘时，根据两者构成的地址从ROM中索取乘积结果。由于ROM可采用分布式逻辑资源实现，也可采用嵌入式Block RAM实现，各有优势，可满足不同场合的需求，故该方法具有一定的灵活性。

两个N bit二进制数相乘，其结果为2N bits，这意味着ROM的深度为\(2^{2N}\)，宽度为2N，占用存储空间大小为\(2^{2N}\times 2N\)。以两个4bit数相乘为例，其存储空间大小为256x8bit，如图3.1所示。无论是有符号数相乘还是无符号数相乘都适用。显然，随着位宽的增长存储空间将以指数速度膨胀。这正是这种方法的一个弊端。

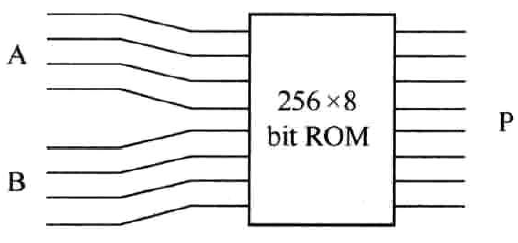
图3.1 以ROM方式实现两个4bit数相乘

由于上述弊端，一种改进方法就是进行位分解，将两个大位宽的数相乘分解为多个小位宽的数相乘。例如，两个4bit数相乘，可将4bit拆分为两个2bit，从而变成四个2bit数相乘。为了保证最终结果的正确，需要对中间四个乘积结果进行移位处理。为方便起见，以两个无符号数(11)x(6)对应二进制(1011)x(0110)相乘为例，以\(H_{1},H_{2}\)分别表示为(1011)和(0110)的高两位，以\(L_{1},L_{2}\)分别表示其低两位，故

\[\begin{aligned} (1011)\times(0110) &= (2^2\cdot H_{1} + L_{1}) \times (2^2\cdot H_{2} + L_{2}) \\ &=2^4 \cdot H_{1}\cdot H_{2} + 2^2\cdot H_{1}\cdot L_{2} + 2^2\cdot H_{2}\cdot L_{2} + L_{1}\cdot L_{2} \end{aligned} \tag{3.1} \]

根据式\((3.1)\)可得其处理流程如图3.2所示。

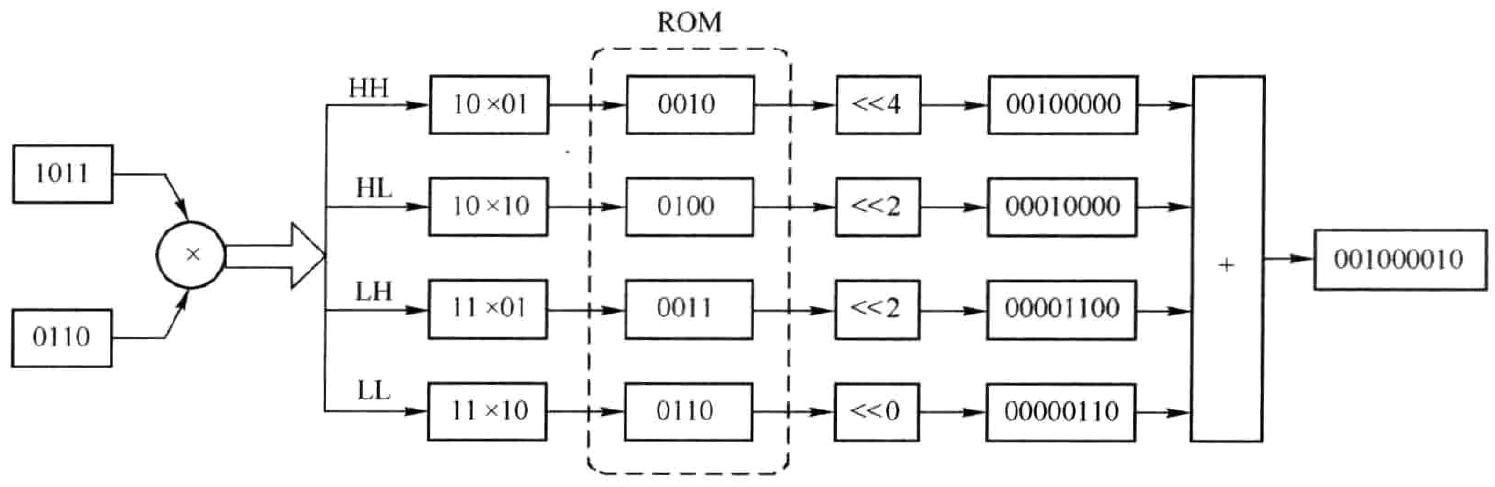
图3.2 相乘的位分解处理流程

图3.2中，\("<<n"\) 表示将输入数据左移n位。基于此设计思想，可得如图3.31所示的硬件电路结构。

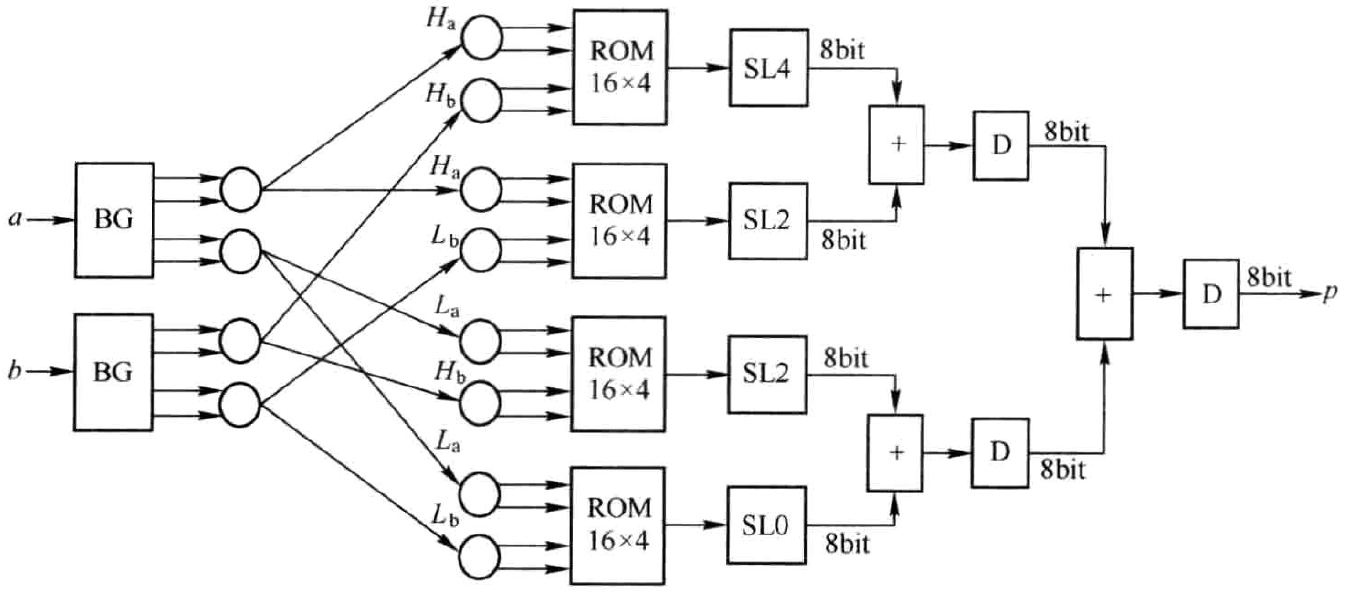
图3.3 利用位分解以多个ROM实现两个4bit无符号数相乘的硬件电路

图3.3中BG模块用于分选出数据的高两位（H）和低两位（L）。四个ROM完全相同，深度均为16，宽度均为4，存储内容均为两个无符号数相乘的结果，如表3.1所示。

表3.1 位分解方式无符号数ROM中存储的内容

地址		内容	地址		内容
00	00	0000	10	00	0000
00	01	0000	10	01	0010
00	10	0000	10	10	0100
00	11	0000	10	11	0110
01	00	0000	11	00	0000
01	01	0001	11	01	0011
01	10	0010	11	10	0110
01	11	0011	11	11	1001

对ROM输出的4bit数据首先要进行高位补零，将其扩展为8bit，以免后续移位操作使有效位移出，这和前文所述乘法原理是完全一致的。SL0表示对数据左移0位，SL2表示对数据左移2位，SL4表示左移4位。得到的部分乘积相加位最终结果。整个结构采用了全流水的方式，可高速运行。与图3.1相比，存储空间由原来的256x8bit变为16x4x4bit，缩减为原来的1/8。可见，此方法对于减小存储空间是非常有利的，此外，也减小了制作ROM存储数据的工作量。

对于有符号数，仍然可以用位分解方式，相应的硬件结构与图3.3完全一致，只是ROM中存储的内容有所不同。以两个4bit有符号数相乘为例，此时需要将每个数的高两位视为有符号数，低两位视为无符号数。ROM中所存储的数据如表3.2所示。可见，\(H_{a}L_{b}\)和\(H_{b}L_{a}\)对应的ROM所存储的内容是一致的。

表3.3 位分解方式有符号数ROM中存储的内容

地址		内容	地址		内容	地址		内容	地址		内容
Ha	Hb		Ha	Lb		Hb	La		La	Lb
00	00	0000	00	00	0000	00	00	0000	00	00	0000
00	01	0000	00	01	0000	00	01	0000	00	01	0000
00	10	0000	00	10	0000	00	10	0000	00	10	0000
00	11	0000	00	11	0000	00	11	0000	00	11	0000
01	00	0000	01	00	0000	01	00	0000	01	00	0000
01	01	0001	01	01	0001	01	01	0001	01	01	0001
01	10	1110	01	10	0010	01	10	0010	01	10	0010
01	11	1111	01	11	0011	01	11	0011	01	11	0011
10	00	0000	10	00	0000	10	00	0000	10	00	0000
10	01	1110	10	01	1110	10	01	1110	10	01	0010
10	10	0100	10	10	1100	10	10	1100	10	10	0100
10	11	0010	10	11	1010	10	11	1010	10	11	0110
11	00	0000	11	00	0000	11	00	0000	11	00	0000
11	01	1111	11	01	1111	11	01	1111	11	01	0011
11	10	0010	11	10	1110	11	10	1110	11	10	0110
11	11	0001	11	11	1101	11	11	1101	11	11	1001

对于有符号数，另一种方法是将其转换为无符号数相乘，使得ROM中所存储数据的制作较为容易。对于最终结果，将两个数的符号位判断是否进行补处理。相应的硬件结构如图3.32所示。这里仍以两个4bit数相乘为例，将其分解为4个2bit数相乘。根据A和B的符号位进行判断，如果符号位为1，则前级两个MUX分别输出A和B求补后结果，否则分别输出A和B。可见，前级两个MUX总是输出|A|和|B|，从而，后续乘法的被乘数和乘数即可当作无符号数，实现了由有符号数相乘到无符号数相乘的转换。这就使得图3.4中的ROM与图3.3中的ROM完全一致，即存储的均为两个2bit无符号数相乘的结果。最终结果prod则要根据A和B的符号位异或(XOR)的结果进行判断。当异或结果为1时，说明A和B有一个为正数，而另一个为负数，故将p求补的结果赋给prod。当异或结果为0时，说明A和B同为正数或同为负数，故将p赋值给prod。

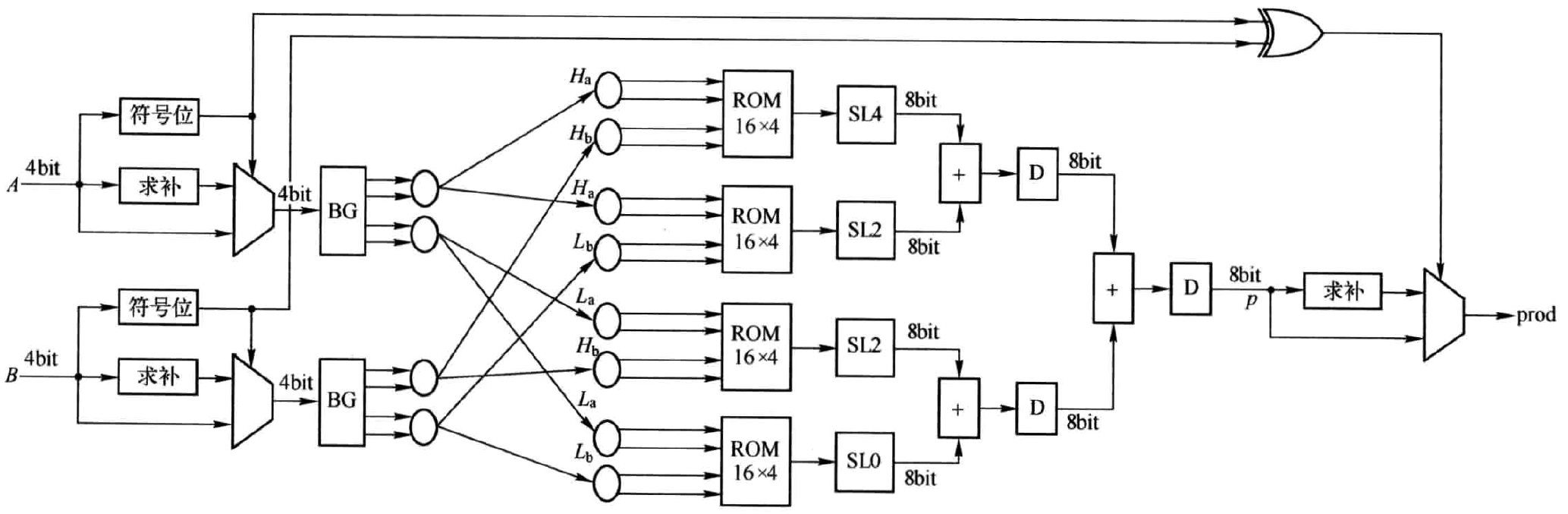
图3.4 采用位分解的两个4bit有符号数相乘的硬件结构

图3.4中四个ROM完全相同：具有相同的深度、相同的宽度和相同的存储内容。从而，可以通过分时复用达到资源共享的目的，节省了资源，而付出的代价就是系统速度的降低。为实现分时复用就需要额外的控制逻辑，以便从输入数据中分时提取ROM地址以索取部分积。整个电路的硬件结构如图3.5所示。图中对输入数据所采取的措施与图3.4中的完全一致，都为同一个目的，即保证第一级MUX输出的是输入数据的绝对值。第二级MUX共四个，每两个一组，在控制信号sel_a和sel_b的作用下分选出前级MUX输出数据的数据位，分时形成四个地址送入ROM的地址输入端。其中，\(A_{i}(i=0,1,2,3)\)是数据|A|的第i位数据，且第0位为LSB，第3位为MSB；相应地，\(B_{i}(i=0,1,2,3)\)是数据|B|的第i位数据。控制模块control输出四个控制信号：第二级MUX的选择信号sel_a和sel_b、移位模块的控制信号shift（控制输入数据左移位数）和捕获寄存器捕获信号capture（捕获累加结果）。

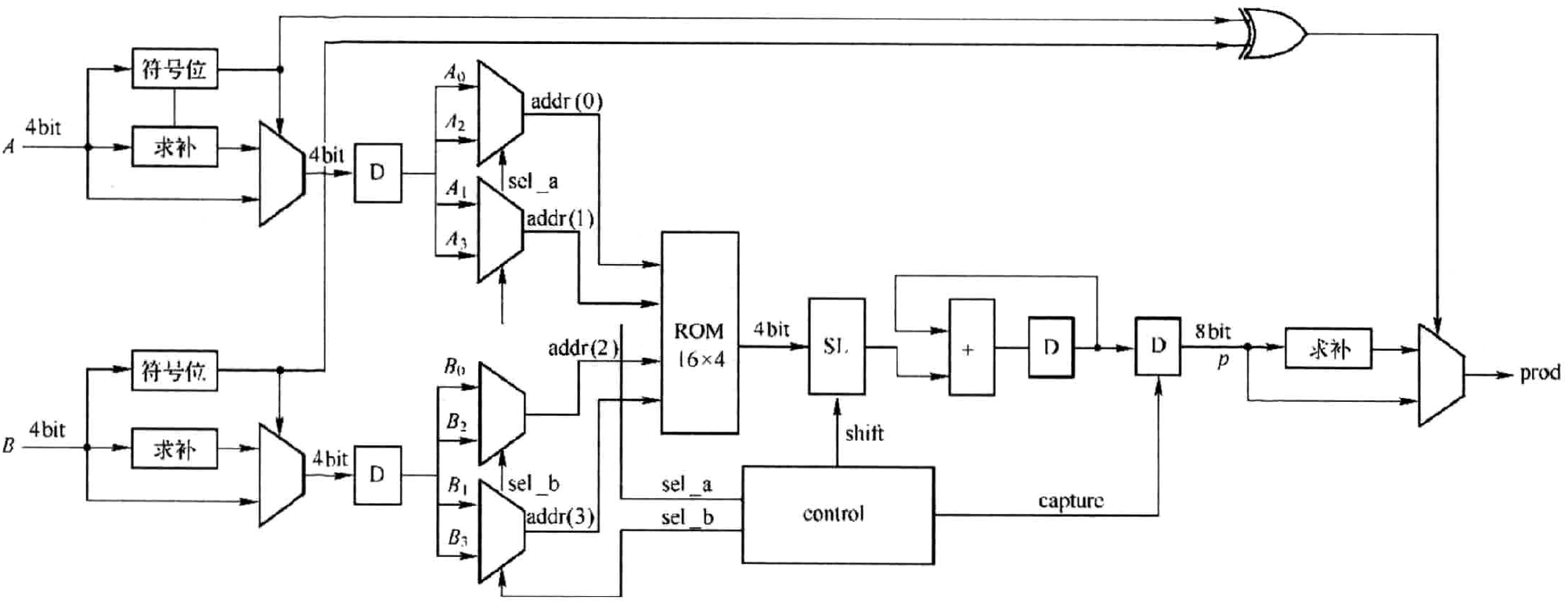
图3.5 采用分时复用位分解的两个4bit有符号数相乘的硬件结构

图3.5中，控制模块输出时序如图3.6所示。控制模块实质是一个模值为4的计数器cnt4,sel_a为cnt4的MSB，sel_b为cnt4的LSB，从而控制四个MUX输出相应的数据构成ROM的地址addr。对cnt4译码产生移位模块的控制信号shift。译码规则为当cnt4为0时，输入数据左移0位；当cnt4为1或2时，输入数据左移2位；当cnt4为3时，输入数据左移4位。捕获信号capture也将通过对cnt4译码产生。此外，需要注意的是此电路后续运算速率是输入数据速率的4倍，这一点在图3.6中也有所体现，这也正是为节省资源所付出的代价。

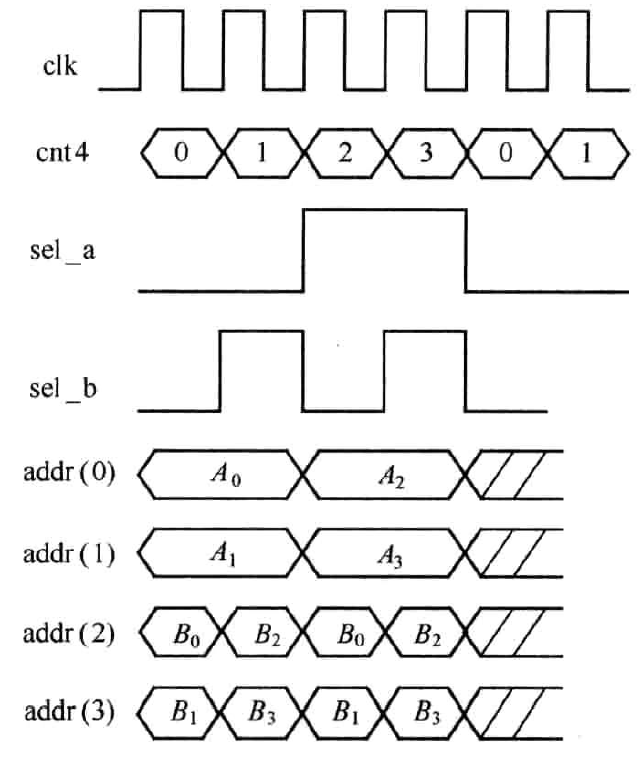
图3.5电路中控制模块输出时序

采用ROM的方式实现乘法实质上是用“人工计算”代替了“FPGA内部计算”，即预先将所有可能的结果存储在ROM中，在通过索引的方式查找相应的乘积。这就必须保证ROM中所存数据的正确性以及数据与地址的匹配性。这种方式也体现了FPGA内部资源配置的灵活性，尽管ROM还是用来存储数据的，但最终实现的却是运算功能。在某些需要较多乘法器的场合，这不失为一种好的选择。

4. 与固定系数相乘的乘法器（KCM）

事实上，在乘法器的使用过程中经常会出现被乘数或者乘数为固定常数的情形，如固定系数的FIR滤波器。以K表示此固定常数，称此类乘法器为固定系数乘法器KCM(K-Constant Coefficient Multiplier)。对于KCM，可根据K的数值特性，设计出具有针对性的乘法器而避免浪费硬线乘法器资源。

采用移位相加的方法可实现KCM。此时，如果K为\(2^n\)或者非常接近\(2^n\)，此方法非常适用。例如，K=9，可将其分解为(\(2^3+1\))，则A与K相乘，即变为将A左移3位再与A相加。假定A为4bit二进制补码，则乘积结果的范围为[-72,63]，可用8bit二进制补码表示。确定了乘积的位宽也就确定了中间数值（移位后的数值）的位宽。图4.1显示了A分别为3和-5的求解过程。图中\("<<3"\)表示将输入数据左移3位，SE表示符号位扩展(Signed Extend)。对于A与K均为无符号数的情形，只需将图中的SE替换为高位补零操作即可。

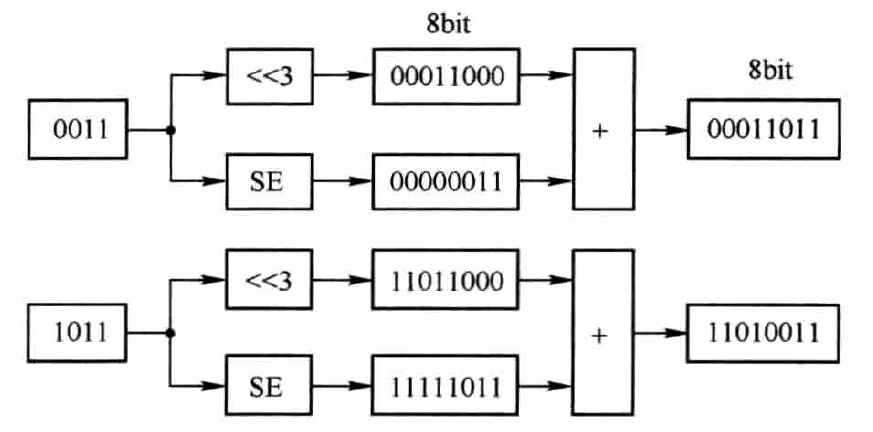
图4.1 K为正数时移位相加的求解过程

当K=-9时，仍可采用上述流程，但需要将上述结果求补，如图4.2所示。

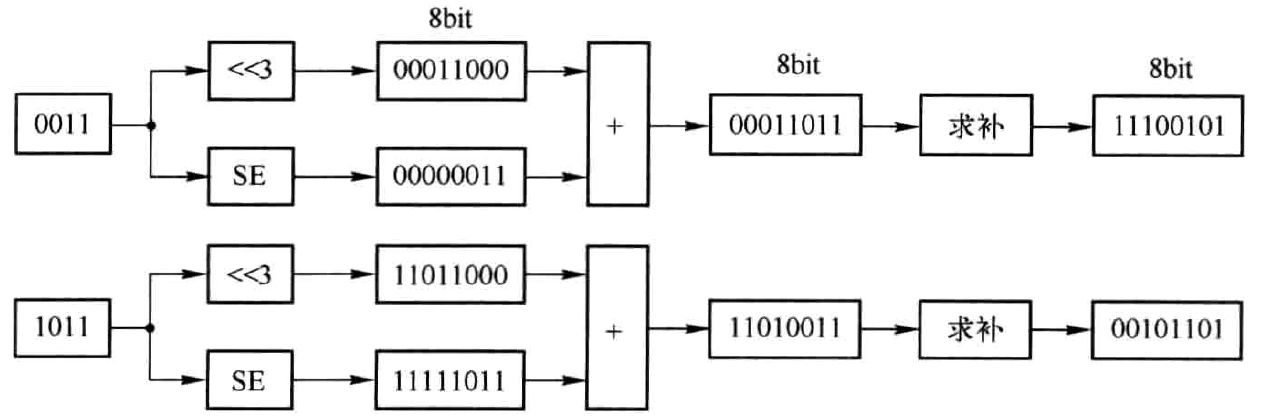
图4.2 K为负数时移位相加的求解过程

当有多个固定系数时，可根据系数特征共享移位单元。

采用ROM的方式也可实现KCM。例如，两个4bit二进制补码数A与K相乘，K为固定常数，假定为7。此时，将A作为ROM的地址输入端，ROM内与地址相对应存储着乘积结果，如图4.3所示。可知乘积结果的取值范围为[-56,49],只需要7位二进制补码表示，与常规的两个4bit数相乘结果为8bit相比，节省了一位。此外，与图3.1相比，ROM的存储空间也从256x8bit变为16x7bit，有很大程度的缩减。当A与K均为无符号数时，仍可采用图4.3所示结构，只需要改动ROM内的存储数据即可。

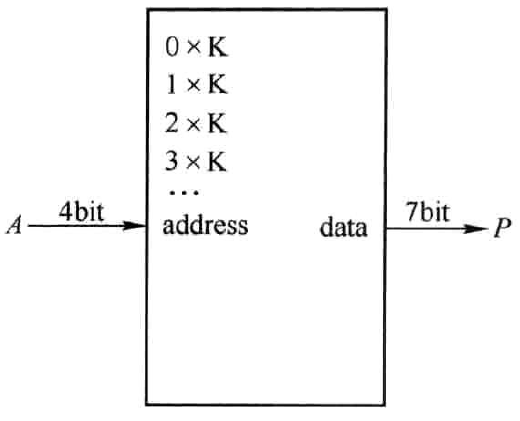
图4.3 采用ROM的方式实现KCM

为进一步缩减存储空间大小，可采取分解的方法。对于无符号数相乘的KCM，仍可采用图3.2所示的处理流程，而对于有符号数相乘的KCM，则需要对其进行一定的改动。为便于说明，仍以两个4bit数A与K相乘为例，且取K=-5，其4位二进制补码为(1011)。将A分为高两位H和低两位L。把L视为无符号数，则L可能的取值为0，1，2和3，L与-5想乘结果分别为0、-5，-10和-15,将它们相应的6位二进制补码存储在ROM_L中。把H视为有符号数，则H可能的取值为0,1,-2和-1，H与-5相乘的结果分别为0，-5，10和5，将它们相应的6位二进制补码存储在ROM_H中。计算时，以L和H分别作为ROM_L和ROM_H的地址索引相应的部分积，对部分积再做进一步处理得到最终结果。整个硬件结构如图4.4所示。如果A=-7，其4位二进制补码为(1001)，则L=01,H=10,故ROM_L输出(11011),ROM_H输出(01010)。进一步，SE模块输出(1111011)，SL模块输出(1110001)，SL模块输出(1101100)，两者相加为(1011101)，对应十进制-35。可见，位分解的实质仍是二进制乘法原理。从图中可以看出存储空间大小为\(4\times 5 \times 2 = 40\)bit。如果不采用位分解，则存储空间大小为\(16\times 7\)=112bit。这也证明了位分解可有效缩减存储空间。

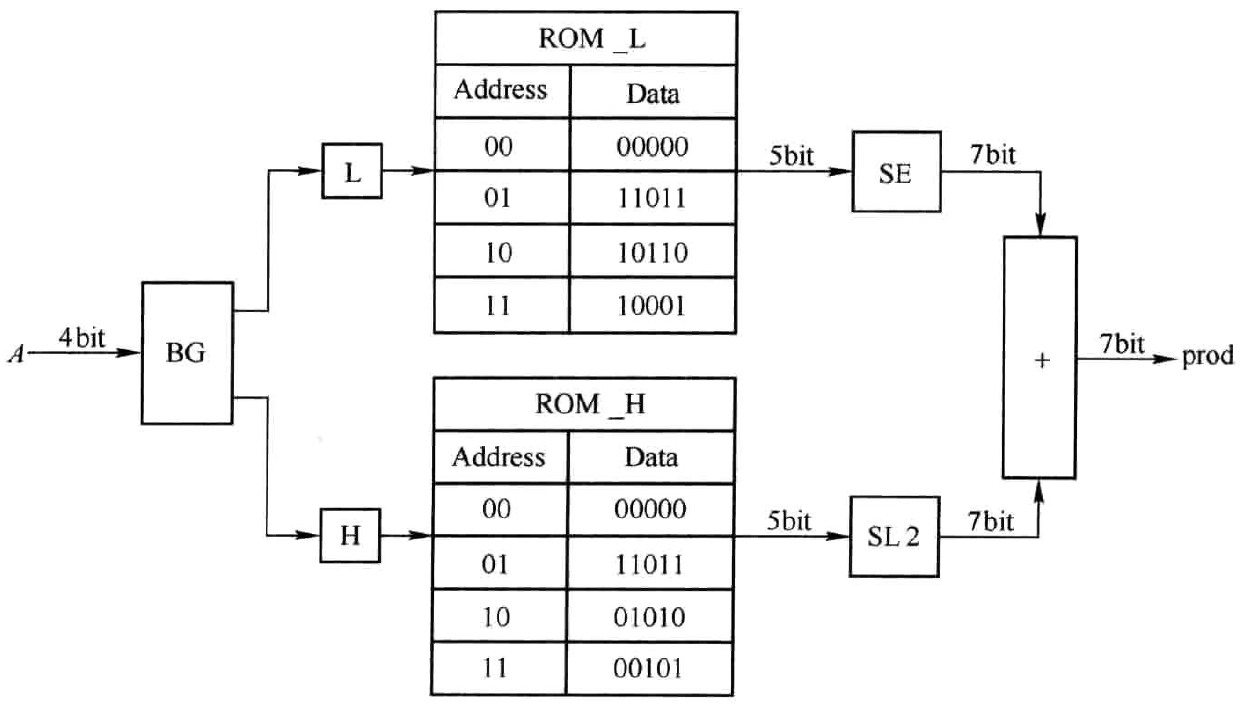
图4.4 采用位分解的KCM

图4.4 所示的方法需要对符号位部分和权值位部分分别制作ROM，显得过于烦琐。为此，可做如下改进，如图4.5所示。其思想是，将A取绝对值与K相乘，对乘积结果根据A的符号位进行修正。输入数据A转换为正数可通过图中的MUX实现，即当A的符号位为１时，MUX输出A求补后的结果，否则输出A，那么MUX输出的数据必然为正数。两个ROM完全一致，存储数据均为0，-5，-10和-15。对于乘积结果，仍需要根据A的符号位判断。当A为负数时，输出prod_temp的补码，否则输出prod_temp。显然，该方法对于K为正数也是适用的。此外，由于图中两个ROM完全一致，故也可采用类似图3.5所示的结构对ROM进行分时复用或者采用双端口ROM以节省资源。

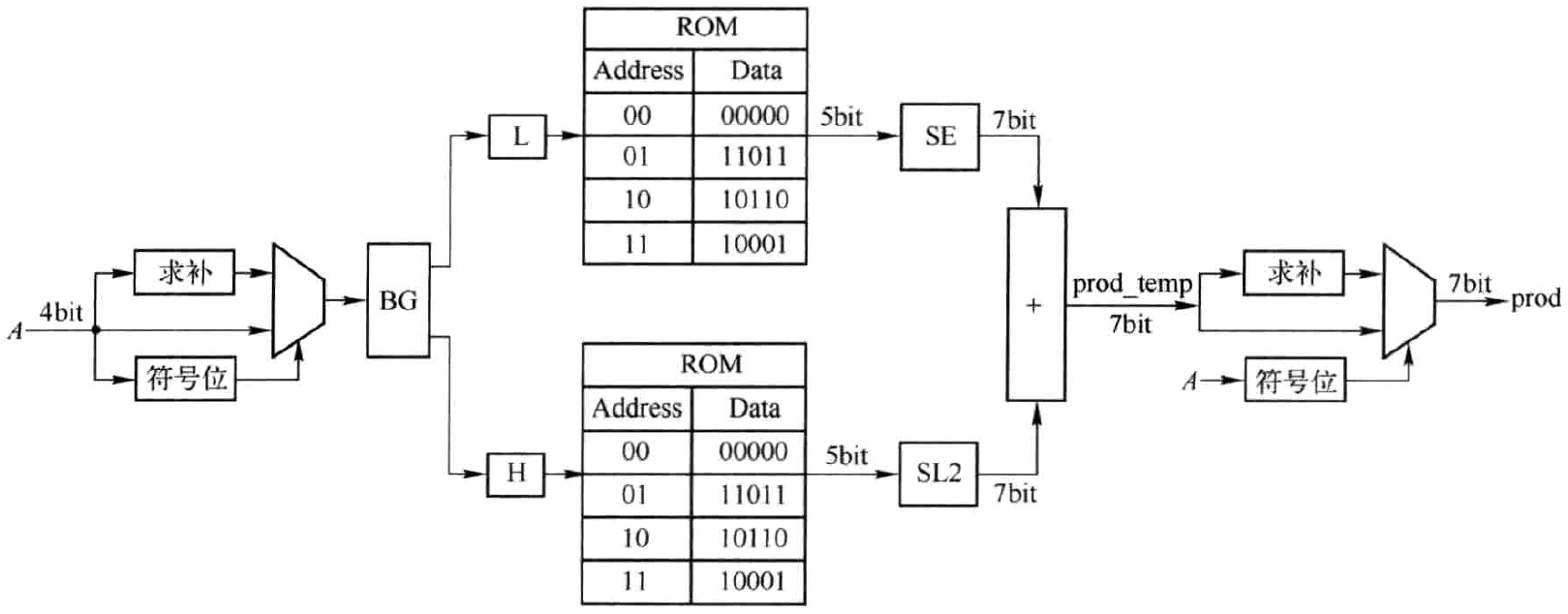
图4.5 将有符号数转换为无符号数采用位分解实现KCM

参考资料：

1. 高亚军，《基于FPGA的数字信号处理》(第二版)，2015；