机器学习之树模型
大纲
- 决策树和回归树模型:ID3, C4.5,CART
- AdaBoost框架
- 提升树:梯度提升树
决策树
决策树模型可以看做是if-else指令集合,通过对特征空间的划分来完成分类或者回归任务。以下图中的分类任务为例,假设数据集包含了:
- 三个类别:黄色、蓝色、绿色
- 两个维度的特征空间:\(x_1, x_2\)
根据if-else规则很容易将特征空间划分为三个区域:\(R_1, R_2, R_3\),对应的决策树如右图所示。也可以先对\(x_1\)进行划分,但是可以证明,先对\(x_1\)进行划分得到的决策树会比示例中的更加复杂,将会产生4个叶子节点,特征空间也会被划分的更加零碎。

特征的划分
从上一部分的示例中可以看出,在决策树的构建中,选取特征维度的何种序列进行划分,都能实现最终的任务。但是如果顺序选取的不合理,得到的决策树的复杂程度会有很大的差异。
一个好的划分维度应该是能够将数据分的足够开,这包含了两个方面:类内差距足够小、类间差距足够大。从示例中可以看出,如果先用\(x_2\)进行划分,绿色类完全被分开,如果先用\(x_1\)进行划分则达不到这种效果。
类内差距小与类内的混乱程度是一致的。衡量混乱程度的指标有很多,比如信息熵、基尼系数、均方误差、方差等。前两个指标通常用在分类任务中,ID3和C4.5采用了信息熵;后两个指标在本质上是一样的,通常用在回归任务中,CART树在分类时采用了基尼系数,在回归任务中采用了均方误差。各类指标的表达式如下:
-
信息熵
\[H(X) = -\sum_{i=1}^N p(x_i)\log p(x_i)
\]
-
基尼系数
\[Gini(X) = \sum_{i=1}^N p(x_i)(1 - p(x_i))
\]
-
均方误差
\[MSE(X) = \sum_{i=1}^N \left(x_i - \bar{X}\right)^2
\]
-
方差
\[Var(X) = \frac{1}{N}\sum_{i=1}^N \left(x_i - \bar{X}\right)^2
\]
在选取划分特征中,是通过比较划分前后数据的混乱程度实现。假设对于分类任务:
- 数据集:\(D\),共包含\(K\)个类别:\(C_1, C_2, ..., C_K\)
- 离散特征\(A\)将\(D\)划分\(n\)个部分:\(D_1, D_2, ..., D_n\),划分后的\(D_i\)中包含各个类别的集合为:\(C_{i1}, C_{i2}, ..., C_{iK}\)
划分前后的信息熵分别记为:\(H(D), H(D|A)\)
\[H(D) = -\sum_{k=1}^K \frac{|C_k|}{|D|}\log\frac{|C_k|}{|D|}\\
H(D|A) = -\sum_{i=1}^n \frac{|D_i|}{|D|} \sum_{k=1}^{K}\frac{|C_{ik}|}{|D_i|}\log\frac{|C_{ik}|}{|D_i|}
\]
计算信息增益
\[g(D, A) = H(D)-H(D|A)
\]
因此最优的划分特征为
\[A^\star = \arg\max_{g\in Dom(A)} g(D, A)
\]
其中Dom(A)表示特征域
对于回归任务:
选取切分特征时,遍历维度\(j\),扫描切分点\(s\)求解下式:
\[\min _{j, s}\left[\min _{c_{1}} \sum_{x_{i} \in R_{1}(j, s)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{x_{i} \in R_{2}(j, s)}\left(y_{i}-c_{2}\right)^{2}\right]
\]
决策树的构建
ID3


回归树

AdaBoost框架
理论基础
AdaBoost的基本思想是通过融合一些弱分类器来提升模型性能。PAC理论证明了一个问题是强可学习的充分必要条件是弱可学习,因此通过结合一些弱学习器来实现强可学习的想法自然而然的诞生。AdaBoost可以认为是不同的学习器侧重学习不同特征,下一个学习器着重学习之前的学习器没有学到的部分,从而实现从数据中抽象出更多的特征。
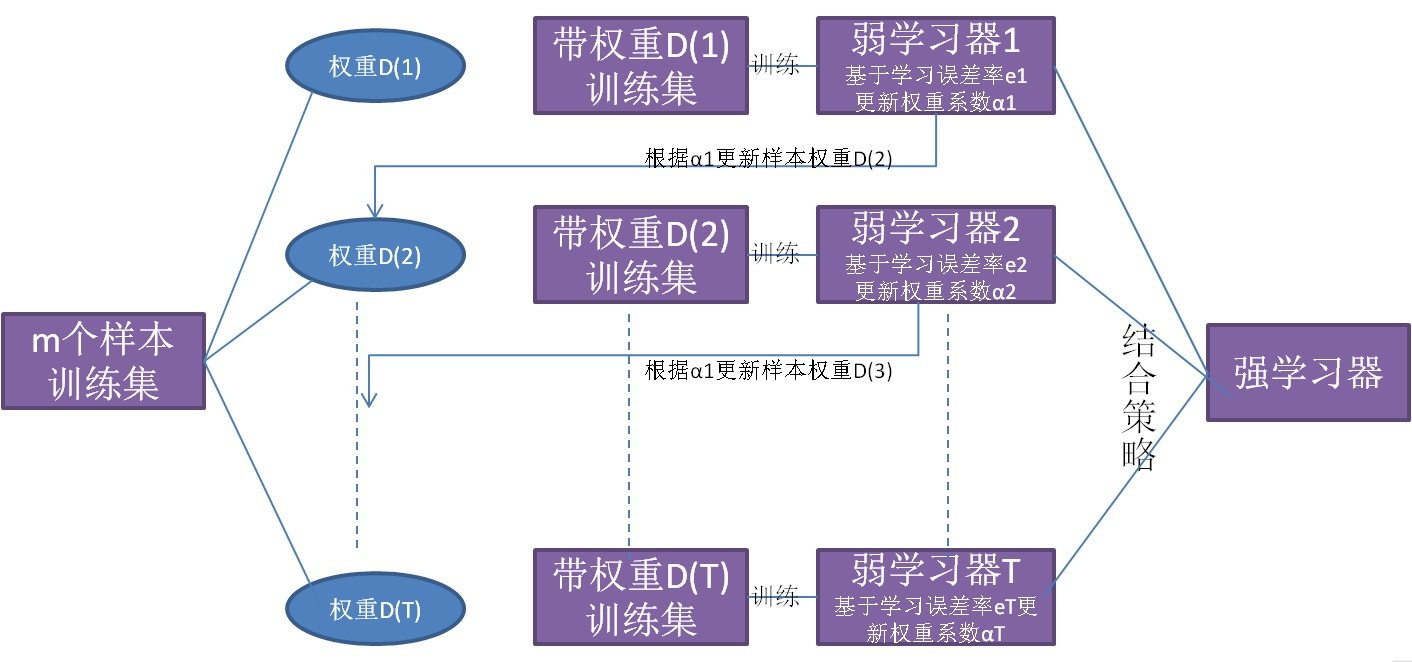
基本构成
AdaBoost框架一般包含如下的部分:
-
基学习器:\(h(x;\theta)\),基学习器一般是弱学习器,弱学习器可易理解为学习效果稍微好于随机猜测
-
融合策略:\(H(x) = \sum_\limits{i=1}^m \alpha_ih(x;\theta_i)\)
-
损失函数(二分类问题):\(\mathcal{L}_{exp}(y, f(x) = \exp(-yf(x))\)
学习策略
AdaBoost的学习过程包括三个部分:
AdaBoost的学习采用了前向算法,即假设前\(i-1\)个部分已经学习完成,然后求解第\(i\)个学习器及其权重。对于第\(i\)个学习器:
\[\begin{align}
\mathcal{L}(y, H_{i}(x)) &= \sum_{j=1}^N\exp\{-y_j (H_{i-1}(x_j) + \alpha h(x_j)\}\\
&= \sum_{j=1}^N \exp\{-y_j (H_{i-1}(x_j)\}\exp\{-y_j \alpha h(x_j)\}\\
&\overset{\Delta}{=} \sum_{j=1}^N \bar{w}_{i, j} \exp\{-y_j\alpha h(x_j)\}\\
&= \sum_{j=1}^N \bar{w}_{i, j} (1 -y_j\alpha h(x_j) + \frac{1}{2}(y_j\alpha h(x_j))^2)\\
&=\sum_{j=1}^N \bar{w}_{i, j} (1+\frac{1}{2}\alpha^2 -y_j\alpha h(x_j))\\
&=\sum_{j=1}^N \bar{w}_{i, j} (1+\frac{1}{2}\alpha^2 -\alpha(1 - 2\mathbb{I}(y_j \neq h(x_j))\\
&= \sum_{j=1}^N \bar{w}_{i, j} (1+\frac{1}{2}\alpha^2 -\alpha + 2\alpha \mathbb{I}(y_j \neq h(x_j))\\
\end{align}
\]
最优学习器\(h_i(x)\)为:
\[h_i(x) = \arg \min \sum_{j=1}^N \bar{w}_{i, j}\mathbb{I}(y_j \neq h(x_j))
\]
从该公式可以看出,对于被\(H_{i-1}(x)\)分错的样本,\(h_i(x)\)会着重学习
\[\begin{aligned}
\mathcal{L}(y, H_i(x)) &= \sum_{j=1}^{N} \bar{w}_{i, j} \exp \left[-y_{j} \alpha h_i\left(x_{j}\right)\right] \\
&=\sum_{y_{j}=h_{i}\left(x_{j}\right)} \bar{w}_{i,j} \mathrm{e}^{-\alpha}+\sum_{y_{j} \neq h_{i}\left(x_{j}\right)} \bar{w}_{i,j} \mathrm{e}^{\alpha} \\
&=\left(\mathrm{e}^{\alpha}-\mathrm{e}^{-\alpha}\right) \sum_{j=1}^{N} \bar{w}_{i,j} \mathbb{I}\left(y_{j} \neq h_i\left(x_{j}\right)\right)+\mathrm{e}^{-\alpha} \sum_{j=1}^{N} \bar{w}_{i,j}
\end{aligned}
\]
学习器\(h_i(x)\)的权重\(\alpha_i\)为:
\[\alpha_i = \frac{1}{2}\log\frac{1-e_{i}}{e_i}
\]
其中\(e_i\)为分类器\(h_i(x)\)的错误率
\[\begin{aligned}
e_{i} &=\frac{\sum_\limits{j=1}^{N} \bar{w}_{i,j} \mathbb{I}\left(y_{j} \neq h_i\left(x_{j}\right)\right)}{\sum_\limits{j=1}^{N} \bar{w}_{i,j}} \\
&=\sum_{j=1}^{N} w_{i,j} \mathbb{I}\left(y_{j} \neq h_i\left(x_{j}\right)\right)
\end{aligned}
\]
从\(\alpha_i\)可以看出,高错误率的子学习器占据的权重较小
数据分布更新:
\[\begin{align}
\bar{w}_{i,j} &= \exp\{-y_jH_{i-1}(x_j)\}\\
H_i(x) &= H_{i-1}(x) + \alpha_i h_i(x)\\
\bar{w}_{i+1, j} &= \exp\{-y_j(H_{i-1}(x_j)+\alpha_i h(x_j))\}\\
&= \bar{w}_{i,j}\exp\{-y_j\alpha_i h(x_j)\}
\end{align}
\]
提升树
提升树主要是用来解决回归任务。将回归树\(T(x) = \sum_\limits{i=1}^{M}\hat{c}_i \mathbb{I}(x\in R_i)\)作为基学习器,对于前向分步:
\[\begin{aligned}
&H_{0}(x)=0\\
&\begin{aligned}
H_{m}(x) &=H_{m-1}(x)+T\left(x ; \Theta_{m}\right), \quad m=1,2, \cdots, M \\
H_{M}(x) &=\sum_{m=1}^{M} T\left(x ; \Theta_{m}\right)
\end{aligned}
\end{aligned}
\]
在第m步时:
\[\begin{align}
\hat{\Theta}_{m}&=\arg \min _{\Theta_{m}} \sum_{i=1}^{N} L\left(y_{i}, H_{m-1}\left(x_{i}\right)+T\left(x_{i} ; \Theta_{m}\right)\right)\\
&=\sum_{i=1}^N\left[y_i-H_{m-1}(x_i)-T\left(x_i ; \Theta_{m}\right)\right]^{2}\\
&=\sum_{i=1}^N\left[r_i-T\left(x_i ; \Theta_{m}\right)\right]^{2}
\end{align}
\]
即在m步时拟合当前的残差即可
在前向算法中,如果采用了平方损失或者指数损失是非常容易实现的,如果采用其他的损失函数将不容易计算。为此采用了类似于梯度下降的思想提出了梯度提升树(GDBT),将采用平方损失的提升树中的残差表达式换为梯度值即可:
\[r_{m i}=-\left[\frac{\partial L\left(y_{i}, h\left(x_{i}\right)\right)}{\partial h\left(x_{i}\right)}\right]_{h(x)=H_{m-1}(x)}
\]







 浙公网安备 33010602011771号
浙公网安备 33010602011771号