凸包小结
先说部分资料来源(蒟蒻也是从他们那里学会的):
数学:凸包算法详解——爱国呐
计算几何之凸包(convexHull)----Graham扫描法——天泽28
话说本来在学斜率优化DP,结果因为某位坑爹博主的一句本来没有问题的话:
是不是很像一个下凸包?
我们用当前的斜率k从下方去不断逼近下凸包,最终会先碰到哪一个点?
我莫名其妙的去学了凸包,觉得学完之后斜率DP说不定能好做点,但是。。。。。。现在依然看不明白。
那么进入正题,先看这样一个例题:

mhr:明显,这个题我们可以暴力枚举!
博主:滚!
可以发现,暴力是绝对不可取的,其实如果这个图就摆在你面前的话,你是很容易就能看出来,栅栏长度就是最外面的一圈点,但是电脑并没有眼睛,所以我们就要使用一些算法来计算出来那外面的一圈,也就是所谓的凸包。有一个比较学术的说法,来自某度某科:
我们有很多不同的方法求出凸包,不过这里介绍的是性价比很高的Graham算法。
graham算法的整个操作基本都在一个栈中完成。如果设所有点的集合为点集Q,那么Q中的所有点都要入栈一次,然后再把一部分不符合要求的点弹出栈,最后剩在栈中的点就是凸包上的点了。
具体实现步骤如下
- 首先我们要选取一个基点o,要求在点集Q中,基点o纵坐标必须是最小的,如果有相同最小的纵坐标,那么选取横坐标最小的,如果还有相同的。。肯定是重点,不用管它就是了。如何快速找到?如果你不嫌麻烦,大可以sort排序之后选第一个,然而实际上,我们只需要找出那个最下面同时是最左边的点就可以了,因为之后整个点集还会重新排序,所以这一开始的顺序没什么用。
-
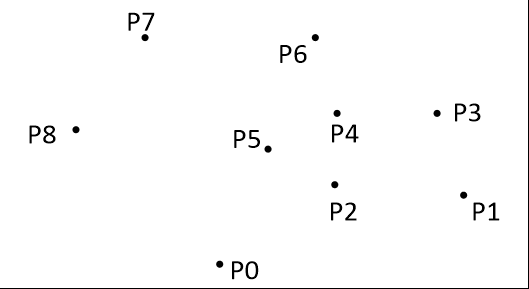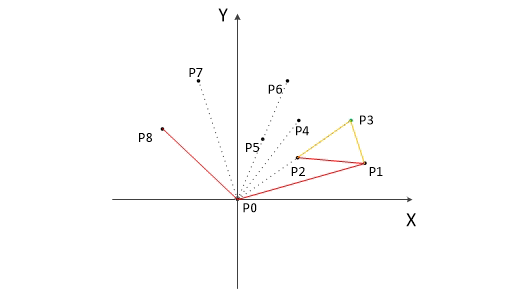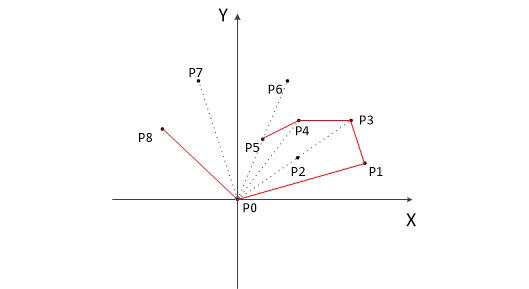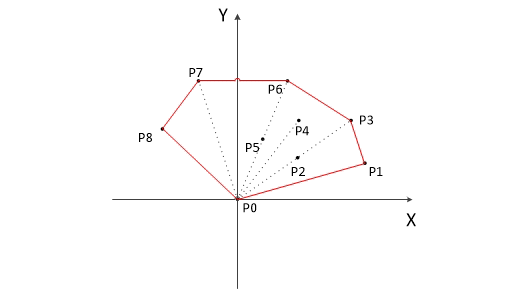
然后我们把剩下的所有点以o为极点,进行极角排序,角小的放在前面,如果角度相同,那么按照到点o的距离排序。
-
设所有的点事p1,p2.....pn。将o,p1,p2三个点压入栈,开始遍历所有剩下的点。
-
对每一个新遍历到的点,很明显我们需要逆时针旋转当前方向,如果有一个点顺时针旋转了,那么我们就把栈顶的点弹出,直到符合逆时针旋转这个要求为止。
看上去十分简明扼要易懂是不是???
读者:打死这个博主,写这些东西我能看懂啥??那个顺时针逆时针我能看出来,电脑那个愚蠢的东西咋看出来??
判断顺时针还是逆时针旋转,我们要用到一个东西——叉积。
好吧又一个新名词。某度某科这么定义叉积:
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用也十分广泛,通常应用于物理学光学和计算机图形学中。
嗯。。。这其实什么也没说明白,这么说吧,貌似博主们和笔者都是一致认为:叉积a×b是点0,a,b和a+b组成的平行四边形的向量面积(也就是有方向的面积)。如果计算出来的叉积是正,那么a在b右侧,否则a在b左侧。如果增添一个公共端点c,那么计算方法就是:(c-a)×(c-b)。P.s可能说的不是很明白,因为笔者对于插入数学公式这种操作还是略不熟练,文章最上方的dalao的博客里有比较清晰地证明。
那么给出算法导论里的证明,还是比较明白的:
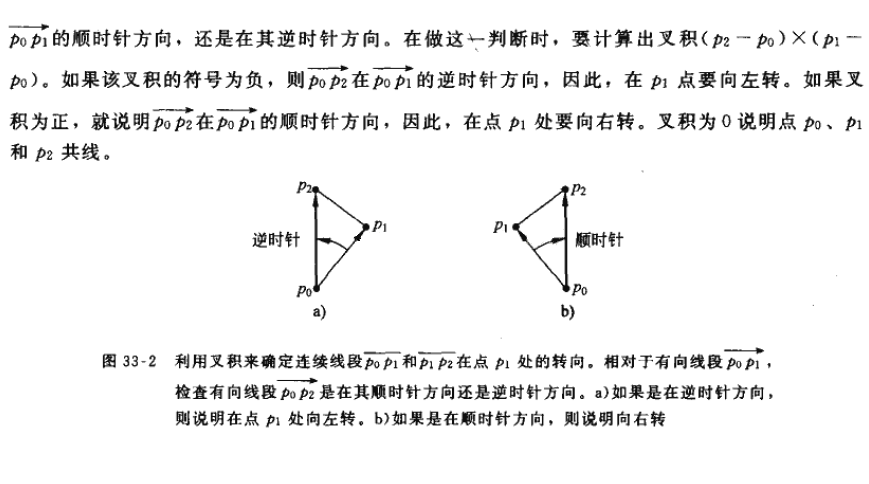
然而其实也有瑕疵,就是这个正负和你计算的顺序是有关系的,经常有不等号写反结果一直爆0的现象发生。所以有句老话“尽信书则不如无书”,不要过分相信书上说的,多实践才是真理。
其实应该手绘静态步骤图的,但是确实是没那个实力,博主从小学开始美术就连B都没得过,全是CD。。。。
那么借来一张动态的给大家看一眼吧:
。
那么基本上大体的就说完了,接下来就是代码了。与往常不同,博主这次会加详细的注释诶:
p.s:以上面那道题目为例。
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #include<queue> #define ll long long #define inf 50000000 #define re register #define MAXN 50005 using namespace std; struct node{ double x,y; }; node a[MAXN],stackk[MAXN]; double xx,yy; int n,top; inline int read() { int x=0,c=1; char ch=' '; while((ch>'9'||ch<'0')&&ch!='-')ch=getchar(); while(ch=='-') c*=-1,ch=getchar(); while(ch<='9'&&ch>='0')x=x*10+ch-'0',ch=getchar(); return x*c; } inline double js(node a,node b)//计算距离自不必说 { return sqrt((a.x-b.x)*(a.x-b.x)*1.0+(a.y-b.y)*(a.y-b.y)*1.0); } inline bool cmp(node a,node b)//第一遍排序,来求基点。 { if(a.y==b.y) return a.x<b.x; return a.y<b.y; } inline double cross(node a,node b,node c)//计算以a为公共端点,b与c的叉积。 { return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y); } inline bool cmp1(node a,node b)//极角排序 { double k=cross(stackk[1],a,b); if(k>0) return 1;//如果b在a时针方向返回1 else if(k==0) return js(stackk[1],a)<=js(stackk[1],b);//如果极角相等,则比较距离 else return 0; } int main() { n=read(); for(re int i=1;i<=n;i++){ scanf("%lf%lf",&a[i].x,&a[i].y); } if(n==1) {printf("0");return 0;} if(n==2) {printf("%.2lf",js(a[1],a[2]));return 0;} sort(a+1,a+n+1,cmp); stackk[++top]=a[1]; xx=stackk[top].x; yy=stackk[top].y; sort(a+2,a+n+1,cmp1); stackk[++top]=a[2]; stackk[++top]=a[3];//把p1,p2,p3压入栈中。 for(re int i=4;i<=n;i++){ while(top>0&&cross(stackk[top-1],stackk[top],a[i])<0)//如果右旋转了,就弹出栈顶的点 top--; stackk[++top]=a[i];//加入新点 } double ans=0; for(re int i=2;i<=top;i++)//点之间两两求距离。 ans+=js(stackk[i-1],stackk[i]); ans+=js(stackk[top],stackk[1]); printf("%.2lf",ans); }
其实也不是很详细了。。。不过笔者自认为码风清晰易懂(逃~~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号