电池温度检测原理和示例代码
一、原理
其实电池内部有个热敏电阻, 与外部分压电阻构成一个简单的分压电路, 根据ADC采样得到的电压j计算热敏阻值再反推此时的温度, 首先我们要先了解热敏电阻阻值和温度一个公式:
/* NTC热敏电阻公式 Rt = R * exp(B*(1/T1-1/T2)) Rt:在T1下的电阻值 T1/T2: 指的是K度,即开尔文温度, T=273.15 + 摄氏度 R: 在T2下的标称阻值,比如在25摄氏度10000欧, T2=273.15 + 25 B:热敏电阻一个参数, 比如3950 exp:e的n次方 我们可以通过温度得到阻值, 也可以通过阻值得到温度 Rt = 10000 * exp(3950*(1/(273.15+t1) - 1/298.15)) t1=1/(ln(Rt/10000)/3950+1/298.15)-273.15 */
我的外部电路如下:
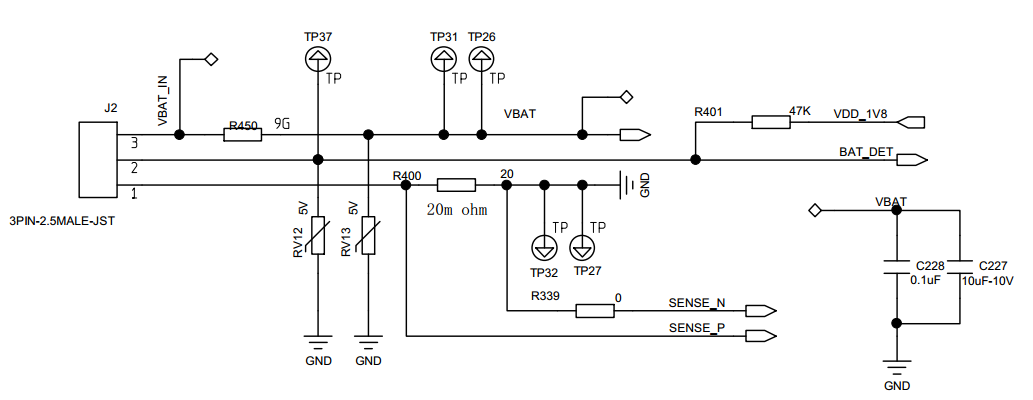
J2是电池插座, 三根线, 中间的就是NTC, BAT_DET连接处理器的ADC采样引脚, 分压电阻阻值47k, 参考电压1.8v, 所以:
Rt = Vadc * Rf / (Vin-Vadc) Vadc: 热敏电阻对应的电压值 Rf: 分压电阻 对应电路47k Vin: 参考电压 1.8v
至于Vadc采样电压就是各个处理器自己的事了, 只要确保采集的电压是准确的, 可以和万用表对比
二、示例代码
下面就演示温度从零下-10度到60度 热敏电阻阻值以及根据采样电压反推热敏电阻的温度, 需要注意的是,代码需要包含math.h函数库的支持, 同时, 数学ln()的叫法在C库是log()
/* gcc test.c -lm */
#include<stdio.h> #include <math.h> int main() {
int t1; double Rt, Vadc; /* 温度从零下-10度到60度 热敏电阻阻值 */ for(t1=-10; t1<60; t1++) { Rt = 10000 * exp(3950*(1/(273.15+t1) - 1/298.15)); Vadc = 1800*Rt/(Rt + 47000); printf("%d = %.10fmv\n", t1, Vadc); } /* 根据采样电压反推热敏电阻的温度 */ for(Vadc=100; Vadc<1000; Vadc+=100) { Rt = Vadc * 47000 / (1800-Vadc); t1=1/(ln(Rt/10000)/3950+1/298.15)-273.15; printf("%.10fmv = %d\n", Vadc, t1); } return 0; }
对应的log:
-10 = 996.1667819082mv -9 = 970.8171351943mv -8 = 945.5463090268mv -7 = 920.3938859522mv -6 = 895.3981112286mv -5 = 870.5956912898mv -4 = 846.0216150692mv -3 = 821.7089994324mv -2 = 797.6889594676mv -1 = 773.9905039042mv 0 = 750.6404554807mv 1 = 727.6633956682mv 2 = 705.0816327966mv 3 = 682.9151923094mv 4 = 661.1818276246mv 5 = 639.8970498688mv 6 = 619.0741746119mv 7 = 598.7243836333mv 8 = 578.8567997063mv 9 = 559.4785723909mv 10 = 540.5949728601mv 11 = 522.2094958620mv 12 = 504.3239670152mv 13 = 486.9386537600mv 14 = 470.0523784230mv 15 = 453.6626319968mv 16 = 437.7656873959mv 17 = 422.3567110965mv 18 = 407.4298722257mv 19 = 392.9784483112mv 20 = 378.9949270420mv 21 = 365.4711035231mv 22 = 352.3981726282mv 23 = 339.7668161643mv 24 = 327.5672846610mv 25 = 315.7894736842mv 26 = 304.4229946520mv 27 = 293.4572401925mv 28 = 282.8814441428mv 29 = 272.6847363289mv 30 = 262.8561923090mv 31 = 253.3848782846mv 32 = 244.2598914134mv 33 = 235.4703957662mv 34 = 227.0056541849mv 35 = 218.8550563020mv 36 = 211.0081429835mv 37 = 203.4546274551mv 38 = 196.1844133667mv 39 = 189.1876100427mv 40 = 182.4545451581mv 41 = 175.9757750675mv 42 = 169.7420930061mv 43 = 163.7445353679mv 44 = 157.9743862542mv 45 = 152.4231804741mv 46 = 147.0827051655mv 47 = 141.9450001930mv 48 = 137.0023574679mv 49 = 132.2473193230mv 50 = 127.6726760645mv 51 = 123.2714628124mv 52 = 119.0369557321mv 53 = 114.9626677478mv 54 = 111.0423438230mv 55 = 107.2699558814mv 56 = 103.6396974382mv 57 = 100.1459779998mv 58 = 96.7834172883mv 59 = 93.5468393367mv 100.0000000000mv = 57 200.0000000000mv = 37 300.0000000000mv = 26 400.0000000000mv = 18 500.0000000000mv = 12 600.0000000000mv = 6 700.0000000000mv = 2 800.0000000000mv = -2 900.0000000000mv = -6
三、其他
a. 数学中对数用log表示,ln表示以e为底数, C库使用log()却表示数学的ln, 如果要表示数学的logab, 由于等效数学的lnb/lna, 即等效C代码log(b)/log(a)
b. ADC采样精度是个问题, 同时最好多次采样取平均值
c. 由于我是要在驱动实现这个功能, 内核没有包含这个math.h和libgcc.a库, 所以参考网上实现了个差不多精度函数:
double ln(double a) { int N = 15; int k,nk; double x,xx,y; x = (a-1)/(a+1); xx = x*x; nk = 2*N+1; y = 1.0/nk; for(k=N;k>0;k--) { nk = nk - 2; y = 1.0/nk+xx*y; } return 2.0*x*y; }
/* https://blog.csdn.net/mike190267481/article/details/7404702 */
对比log如下:
printf("%.10f, %.10f\n", ln(0.1), log(0.1)); printf("%.10f, %.10f\n", ln(1), log(1)); printf("%.10f, %.10f\n", ln(5), log(5)); printf("%.10f, %.10f\n", ln(10), log(10)); printf("%.10f, %.10f\n", ln(15), log(15)); printf("%.10f, %.10f\n", ln(20), log(20)); -2.3023645999, -2.3025850930 0.0000000000, 0.0000000000 1.6094377510, 1.6094379124 2.3023645999, 2.3025850930 2.7053425934, 2.7080502011 2.9856609824, 2.9957322736
尴尬的是内核不支持浮点运算, 所以这个在应用程序调试OK的ln()函数作废, 只能先在应用程序打出各个采样电压对应的温度, 做成一个表格, 然后驱动再根据电压查询表格得到对应温度了
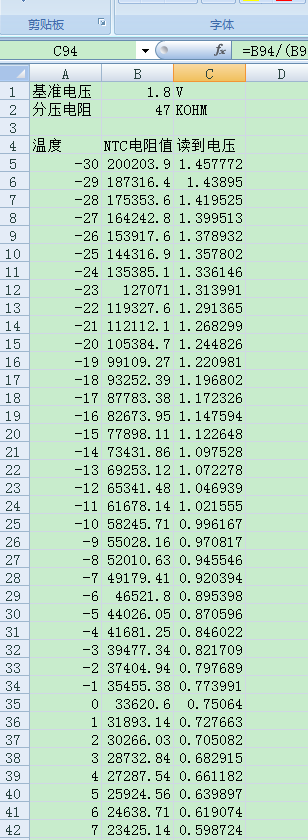
至于为何内核不能进行浮点运算, 这是另一个问题了, 可以参考我另一篇博文:




 浙公网安备 33010602011771号
浙公网安备 33010602011771号