【转载】Hessian矩阵与多元函数极值

转自：https://blog.csdn.net/baimafujinji/article/details/51167852

海塞矩阵（Hessian Matrix），又译作海森矩阵，是一个多元函数的二阶偏导数构成的方阵。尽管它是一个具有悠久历史的数学成果，但是在机器学习和图像处理（例如SIFT和SURF特征检测）中，我们也常常遇到它。所以本文就来向读者道一道Hessian Matrix的来龙去脉。本文的主要内容包括：

• 多元函数极值问题
• 泰勒展开式与Hessian矩阵

---

多元函数极值问题

回想一下我们是如何处理一元函数求极值问题的。例如，f(x)=x2$f(x)=x^2$，我们会先求一阶导数，即f′(x)=2x$f^{\prime }(x)=2x$，根据费马定理极值点处的一阶导数一定等于 0$0$。但这仅是一个必要条件，而非充分条件。对于f(x)=x2$f(x)=x^2$来说，函数的确在一阶导数为零的点取得了极值，但是对于f(x)=x3$f(x)=x^3$来说，显然只检查一阶导数是不足以下定论的。

这时我们需要再求一次导，如果二阶导数 f′′<0$f^{″}<0$，那么说明函数在该点取得局部极大值；如果二阶导数 f′′>0$f^{″}>0$，则说明函数在该点取得局部极小值；如果 f′′=0$f^{″}=0$，则结果仍然是不确定的，我们就不得不再通过其他方式来确定函数的极值性。

如果要在多元函数中求极值点，方法与此类似。作为一个示例，不妨用一个三元函数 f=f(x,y,z)$f=f(x,y,z)$ 来作为示例。首先要对函数中的每个变量分别求偏导数，这会告诉我们该函数的极值点可能出现在哪里。即

∂f∂x=0∂f∂y=0∂f∂x=0$$\begin{gathered} \frac{\mathrm{\partial }f}{\mathrm{\partial }x}=0 \\ \frac{\mathrm{\partial }f}{\mathrm{\partial }y}=0 \\ \frac{\mathrm{\partial }f}{\mathrm{\partial }x}=0 \end{gathered}$$

接下来，要继续求二阶导数，此时包含混合偏导数的情况一共有 9$9$ 个，如果用矩阵形式来表示的话就得到

H=⎡⎣⎢⎢⎢⎢⎢∂2f∂x∂x∂2f∂y∂x∂2f∂z∂x∂2f∂x∂y∂2f∂y∂y∂2f∂z∂y∂2f∂x∂z∂2f∂y∂z∂2f∂z∂z⎤⎦⎥⎥⎥⎥⎥$$\mathbf{H}=\left[\begin{array}{ccc}\frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }x\mathrm{\partial }x}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }x\mathrm{\partial }y}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }x\mathrm{\partial }z}\\ \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }y\mathrm{\partial }x}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }y\mathrm{\partial }y}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }y\mathrm{\partial }z}\\ \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }z\mathrm{\partial }x}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }z\mathrm{\partial }y}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }z\mathrm{\partial }z}\end{array}\right]$$

这个矩阵就称为Hessian矩阵。当然上面所给出的仅仅是一个三阶的Hessian矩阵。稍作扩展，我们可以对一个在定义域内二阶连续可导的实值多元函数 f(x1,x2,⋯,xn)$f(x_1,x_2,\cdots ,x_n)$ 定义其Hessian矩阵H$\mathbf{H}$如下

H=⎡⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢∂2f∂x21∂2f∂x2∂x1⋮∂2f∂xn∂x1∂2f∂x1∂x2∂2f∂x22⋮∂2f∂xn∂x2⋯⋯⋱⋯∂2f∂x1∂xn∂2f∂x2∂xn⋮∂2f∂x2n⎤⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥$$\mathbf{H}=\left[\begin{array}{cccc}\frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_1^2}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_1\mathrm{\partial }{x}_2}& \cdots & \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_1\mathrm{\partial }{x}_n}\\ \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_2\mathrm{\partial }{x}_1}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_2^2}& \cdots & \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_2\mathrm{\partial }{x}_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_n\mathrm{\partial }{x}_1}& \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_n\mathrm{\partial }{x}_2}& \cdots & \frac{{\mathrm{\partial }}^{2}f}{\mathrm{\partial }{x}_n^2}\end{array}\right]$$

当一元函数的二阶导数等于 0$0$ 时，我们并不能确定函数在该点的极值性。类似地，面对Hessian矩阵，仍然存在无法断定多元函数极值性的的情况，即当Hessian矩阵的行列式为 0$0$ 时，我们无法确定函数是否能取得极值。甚至我们可能会得到一个鞍点，也就是一个既非极大值也非极小值的的点。

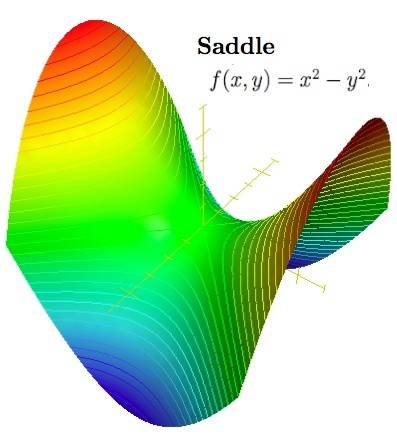
基于Hessian矩阵，就可以判断多元函数的极值情况了，结论如下

• 如果是正定矩阵，则临界点处是一个局部极小值
• 如果是负定矩阵，则临界点处是一个局部极大值
• 如果是不定矩阵，则临界点处不是极值

如何判断一个矩阵是否是正定的，负定的，还是不定的呢？一个最常用的方法就是顺序主子式。实对称矩阵为正定矩阵的充要条件是的各顺序主子式都大于零。当然这个判定方法的计算量比较大。对于实二次型矩阵还有一个判定方法：实二次型矩阵为正定二次型的充要条件是的矩阵的特征值全大于零。为负定二次型的充要条件是的矩阵的特征值全小于零，否则是不定的。

如果你对二次型的概念仍然不很熟悉，这里也稍作补充。定义含有 n$n$
个变量 x1,x2,⋯,xn$x_1,x_2,\cdots ,x_n$ 的二次齐次函数

f(x1,x2,⋯,xn)=a11x21+a22x22+⋯+annx2n+2a12x1x2+2a13x1x3+⋯+2an−1,nxn−1xn$$f(x_1,x_2,\cdots ,x_n)=a_{11}{x}_1^2+a_{22}{x}_2^2+\cdots +a_{nn}{x}_n^2+2a_{12}{x}_1{x}_2+2a_{13}{x}_1{x}_3+\cdots +2a_{n-1,n}{x}_{n-1}{x}_n$$

为二次型。取 aij=aji$a_{ij}=a_{ji}$，则 2aijxixj+ajixjxi$2a_{ij}{x}_i{x}_j+a_{ji}{x}_j{x}_i$，于是上式可以写成

f==a11x21+a12x1x2+⋯+a1nx1xn+a21x2x1+a22x22+⋯+a2nx2xn+⋯+an1xnx1+an2xnx2+⋯+annx2n∑i,j=1naijxixj$$\begin{array}{rl}f=& a_{11}{x}_1^2+a_{12}{x}_1{x}_2+\cdots +a_{1n}{x}_1{x}_n\\ & +a_{21}{x}_2{x}_1+a_{22}{x}_2^2+\cdots +a_{2n}{x}_2{x}_n+\cdots \\ & +a_{n1}{x}_n{x}_1+a_{n2}{x}_n{x}_2+\cdots +a_{nn}{x}_n^2\\ =& \sum _{i,j=1}^n{a}_{ij}{x}_i{x}_j\end{array}$$

更进一步，如果用矩阵对上式进行改写，则有

f===x1(a11x1+a12x2+⋯+a1nxn)+x2(a21x1+a22x2+⋯+a2nxn)+⋯+xn(an1x1+an2x2+⋯+annxn)(x1,x2,⋯,xn)⎡⎣⎢⎢⎢⎢a11x1+a12x2+⋯+a1nxna21x1+a22x2+⋯+a2nxn⋮an1x1+an2x2+⋯+annxn⎤⎦⎥⎥⎥⎥(x1,x2,⋯,xn)⎡⎣⎢⎢⎢⎢⎢a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎤⎦⎥⎥⎥⎥⎥⎡⎣⎢⎢⎢⎢x1x2⋮xn⎤⎦⎥⎥⎥⎥$$\begin{array}{rl}f=& x_1(a_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n)+\\ & x_2(a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n)+\cdots +\\ & x_n(a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n)\\ =& (x_1,x_2,\cdots ,x_n)\left[\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n\\ ⋮\\ a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n\end{array}\right]\\ =& (x_1,x_2,\cdots ,x_n)\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]\end{array}$$

记

A=⎡⎣⎢⎢⎢⎢⎢a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎤⎦⎥⎥⎥⎥⎥,x=⎡⎣⎢⎢⎢⎢x1x2⋮xn⎤⎦⎥⎥⎥⎥$$\mathbf{A}=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1n}\\ a_{21}& a_{22}& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{n1}& a_{n2}& \cdots & a_{nn}\end{array}\right],\mathbf{x}=\left[\begin{array}{c}{x}_1\\ x_2\\ ⋮\\ x_n\end{array}\right]$$

则二次型可记作 f=xTAx$f={\mathbf{x}}^T\mathbf{A}\mathbf{x}$，其中 A$\mathbf{A}$为对称阵。
设有二次型 f=xTAx$f={\mathbf{x}}^T\mathbf{A}\mathbf{x}$，如果对任何 x≠0$x\ne 0$，都有 f>0$f>0$，则称 f$f$ 为正定二次型，并称对称矩阵 A$\mathbf{A}$ 是正定的；如果对任何 x≠0$x\ne 0$，都有 f<0$f<0$，则称 f$f$ 为负定二次型，并称对称矩阵 A$\mathbf{A}$ 是负定的。
正定矩阵一定是非奇异的。对阵矩阵 A$\mathbf{A}$ 为正定的充分必要条件是： A$\mathbf{A}$ 的特征值全为正。由此还可得到下面这个推论：对阵矩阵 A$\mathbf{A}$ 为正定的充分必要条件是 A$\mathbf{A}$ 的各阶主子式都为正。如果将正定矩阵的条件由 xTAx>0${\mathbf{x}}^T\mathbf{A}\mathbf{x}>0$ 弱化为 xTAx≥0${\mathbf{x}}^T\mathbf{A}\mathbf{x}\ge 0$，则称对称矩阵 A$\mathbf{A}$ 是半正定的。

---

泰勒展开式与Hessian矩阵

主页君已经在之前的《图像处理中的数学原理详解》系列文章中介绍过泰勒展开式了。但那个时候我们给出的是一元函数的泰勒公式，不妨先来复习一下。
设一元函数 f(x)$f(x)$ 在包含点x0$x_0$的开区间 (a,b)$(a,b)$ 内具有 n+1$n+1$ 阶导数，则当 x∈(a,b)$x\in (a,b)$ 时，有

f(x)=f(x0)+f′(x0)(x−x0)+f′′(x0)2!(x−x0)2+⋯+f(n)(x0)n!(x−x0)n+Rn(x)$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{″}(x_0)}{2!}(x-x_0{)}^2+\cdots +\frac{f^{(n)}(x_0)}{n!}(x-x_0{)}^n+R_n(x)$$

其中

Rn(x)=f(n+1)(ξ)(n+1)!(x−x0)n+1$$R_n(x)=\frac{f^{(n+1)}(\xi )}{(n+1)!}(x-x_0{)}^{n+1}$$

并且，ξ$\xi$ 在 x$x$ 和 x0$x_0$之间，这被称作是拉格朗日余项。上式被称为 f(x)$f(x)$ 的 n$n$ 阶泰勒公式。在不需要余项的精确表达式时，Rn(x)$R_n(x)$ 可以记作 o[(x−x0)n]$o[(x-x_0{)}^n]$，这被称为是皮亚诺余项。

现在我们把上面这个结论稍微做一下推广，从而给出二元函数的泰勒公式。设二元函数 z=f(x,y)$z=f(x,y)$ 在点 (x0,y0)$(x_0,y_0)$ 的某一邻域内连续且有直到 n+1$n+1$ 阶的连续偏导数，则有

f(x,y)=f(x0,y0)+[(x−x0)∂∂x+(y−y0)∂∂y]f(x0,y0)+12![(x−x0)∂∂x+(y−y0)∂∂y]2f(x0,y0)+⋯++1n![(x−x0)∂∂x+(y−y0)∂∂y]nf(x0,y0)+1(n+1)f[x0+θ(x−x0),y0+θ(y−y0)]$$\begin{array}{rl}f(x,y)& =f(x_0,y_0)+[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}]f(x_0,y_0)\\ & +\frac{1}{2!}[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}{]}^{2}f(x_0,y_0)+\cdots +\\ & +\frac{1}{n!}[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}{]}^{n}f(x_0,y_0)\\ & +\frac{1}{(n+1)!}[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}{]}^{(n+1)}f[x_0+\theta (x-x_0),y_0+\theta (y-y_0)]\end{array}$$

其中，0<θ<1$0<\theta <1$，记号

[(x−x0)∂∂x+(y−y0)∂∂y]f(x0,y0)$$[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}]f(x_0,y_0)$$

表示

(x−x0)fx(x0,y0)+(y−y0)fy(x0,y0)$$(x-x_0)f_x(x_0,y_0)+(y-y_0)f_y(x_0,y_0)$$

记号

[(x−x0)∂∂x+(y−y0)∂∂y]2f(x0,y0)$$[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}{]}^{2}f(x_0,y_0)$$

表示

(x−x0)2fxx(x0,y0)+2(x−x0)(y−y0)fxy(x0,y0)+(y−y0)2fyy(x0,y0)$$(x-x_0{)}^2{f}_{xx}(x_0,y_0)+2(x-x_0)(y-y_0)f_{xy}(x_0,y_0)+(y-y_0{)}^2{f}_{yy}(x_0,y_0)$$

一般地，记号

[(x−x0)∂∂x+(y−y0)∂∂y]mf(x0,y0)$$[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}{]}^{m}f(x_0,y_0)$$

表示

∑p=0mCpm(x−x0)p(y−y0)(m−p)∂mf∂xp∂y(m−p)∣∣∣(x0,y0)$$\sum _{p=0}^m{C}_m^p(x-x_0{)}^p(y-y_0{)}^{(m-p)}\frac{{\mathrm{\partial }}^{m}f}{\mathrm{\partial }{x}^p\mathrm{\partial }{y}^{(m-p)}}{|}_{(x_0,y_0)}$$

当然，我们可以用一种更加简洁的形式来重写上面的和式，则有

f(x,y)=∑k=0n1k![(x−x0)∂∂x+(y−y0)∂∂y]kf(x0,y0)+1(n+1)f[x0+θ(x−x0),y0+θ(y−y0)],(0<θ<1)$$\begin{array}{rl}f(x,y)& =\sum _{k=0}^n\frac{1}{k!}[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}{]}^{k}f(x_0,y_0)\\ & +\frac{1}{(n+1)!}[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}{]}^{(n+1)}f[x_0+\theta (x-x_0),y_0+\theta (y-y_0)],(0<\theta <1)\end{array}$$

当余项Rn(x,y)$R_n(x,y)$采用上面这种形式时称为拉格朗日余项，如果采用皮亚诺余项，则二元函数的泰勒公式可以写成

f(x,y)=∑k=0n1k![(x−x0)∂∂x+(y−y0)∂∂y]kf(x0,y0)+o(ρn)$$f(x,y)=\sum _{k=0}^n\frac{1}{k!}[(x-x_0)\frac{\mathrm{\partial }}{\mathrm{\partial }x}+(y-y_0)\frac{\mathrm{\partial }}{\mathrm{\partial }y}{]}^{k}f(x_0,y_0)+o({\rho }^n)$$

特别低，对于一个多维向量 X$\mathbf{X}$, 以及在点 X0${\mathbf{X}}_0$ 的邻域内有连续二阶偏导数的多元函数 f(X)$f(\mathbf{X})$ ，可以写出该函数在点 X0${\mathbf{X}}_0$ 处的（二阶）泰勒展开式

f(X)=f(X0)+(X−X0)T∇f(X0)+12!(X−X0)T∇2f(X0)(X−X0)+o(∥X−X0∥2)$$f(\mathbf{X})=f({\mathbf{X}}_0)+(\mathbf{X}-{\mathbf{X}}_0{)}^T\mathrm{\nabla }f({\mathbf{X}}_0)+\frac{1}{2!}(\mathbf{X}-{\mathbf{X}}_0{)}^T{\mathrm{\nabla }}^{2}f({\mathbf{X}}_0)(\mathbf{X}-{\mathbf{X}}_0)+o(\Vert \mathbf{X}-{\mathbf{X}}_0{\Vert }^2)$$

其中，o(∥X−X0∥2)$o(\Vert \mathbf{X}-{\mathbf{X}}_0{\Vert }^2)$ 是高阶无穷小表示的皮亚诺余项。而 ∇2f(X0)${\mathrm{\nabla }}^{2}f({\mathbf{X}}_0)$ 显然就是一个Hessian矩阵。所以上述式子也可以写成

f(X)=f(X0)+(X−X0)T∇f(X0)+12(X−X0)TH(X0)(X−X0)+o(∥X−X0∥2)$$f(\mathbf{X})=f({\mathbf{X}}_0)+(\mathbf{X}-{\mathbf{X}}_0{)}^T\mathrm{\nabla }f({\mathbf{X}}_0)+\frac{1}{2}(\mathbf{X}-{\mathbf{X}}_0{)}^T\mathbf{H}({\mathbf{X}}_0)(\mathbf{X}-{\mathbf{X}}_0)+o(\Vert \mathbf{X}-{\mathbf{X}}_0{\Vert }^2)$$

我们已经知道对于 n$n$ 元函数 u=f(x1,x2,⋯,xn)$u=f(x_1,x_2,\cdots ,x_n)$在点 M$M$ 处有极值，则有

∇f(M)={∂f∂x1,∂f∂x2,⋯,∂f∂xn}M=0$$\mathrm{\nabla }f(M)={\left\{\frac{\mathrm{\partial }f}{\mathrm{\partial }{x}_1},\frac{\mathrm{\partial }f}{\mathrm{\partial }{x}_2},\cdots ,\frac{\mathrm{\partial }f}{\mathrm{\partial }{x}_n}\right\}}_M=0$$

也就是说这是一个必要条件，而充分条件则由上一节中之结论给出 。