概率论10 方差与标准差

作者：Vamei 出处：http://www.cnblogs.com/vamei 欢迎转载，也请保留这段声明。谢谢！

 

除了期望，方差(variance)是另一个常见的分布描述量。如果说期望表示的是分布的中心位置，那么方差就是分布的离散程度。方差越大，说明随机变量取值越离散。

 

比如射箭时，一个优秀的选手能保持自己的弓箭集中于目标点附近，而一个经验不足的选手，他弓箭的落点会更容易散落许多地方。

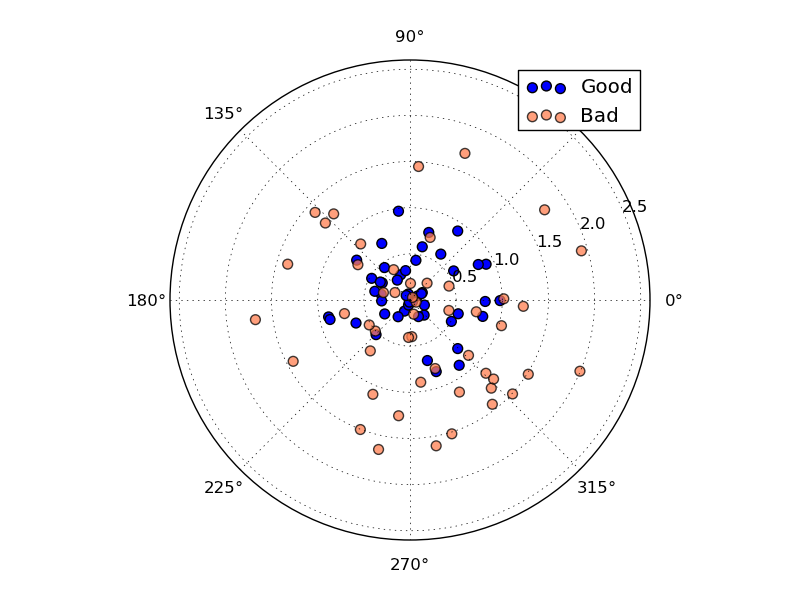
上面的靶上有两套落点。尽管两套落点的平均中心位置都在原点 (即期望相同），但两套落点的离散程度明显有区别。蓝色的点离散程度更小。

 

数学上，我们用方差来代表一组数据或者某个概率分布的离散程度。可见，方差是独立于期望的另一个对分布的度量。两个分布，完全可能有相同的期望，而方差不同，正如我们上面的箭靶。

 

方差

对于一个随机变量[$X$]来说，它的方差为:

$$Var(X) = E[(X - \mu)^2]$$

其中，[$\mu$]表示[$X$]的期望值，即[$\mu = E(X)$]。

 

我们可以代入期望的数学表达形式。比如连续随机变量：

$$Var(X) = E[(X - \mu)^2] = \int_{-\infty}^{+\infty}(x-\mu)^2 f(x)dx$$

 

方差概念背后的逻辑很简单。一个取值与期望值的“距离”用两者差的平方表示。该平方值表示取值与分布中心的偏差程度。平方的最小取值为0。当取值与期望值相同时，此时不离散，平方为0，即“距离”最小；当随机变量偏离期望值时，平方增大。由于取值是随机的，不同取值的概率不同，我们根据概率对该平方进行加权平均，也就获得整体的离散程度——方差。

 

方差的平方根称为标准差(standard deviation, 简写std)。我们常用[$\sigma$]表示标准差

$$\sigma = \sqrt{Var(X)}$$

标准差也表示分布的离散程度。

 

正态分布的方差 

根据上面的定义，可以算出正态分布

$$E(X) = \frac{1}{\sigma \sqrt{2 \pi}}\int_{-\infty}^{+\infty}xe^{-(x - \mu)^2/2 \sigma^2} dx$$

的方差为

$$Var(X) = \sigma^2$$

正态分布的标准差正等于正态分布中的参数[$\sigma$]。这正是我们使用字母[$\sigma$]来表示标准差的原因！

 

可以预期到，正态分布的[$\sigma$]越大，分布离散越大，正如我们从下面的分布曲线中看到的:

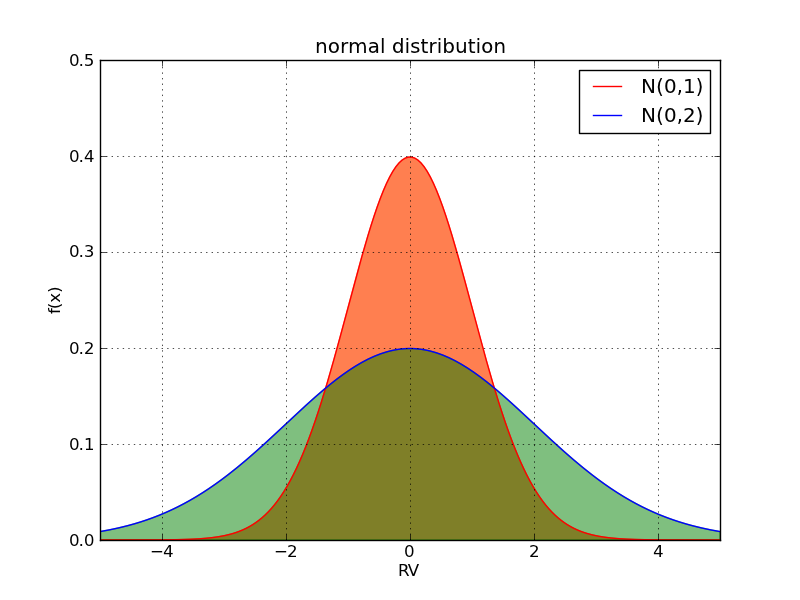当方差小时，曲线下的面积更加集中于期望值0附近。当方差大时，随机变量更加离散。此时分布曲线的“尾部”很厚，即使在取值很偏离0时，比如[$x=4$]时，依然有很大的概率可以取到。

 

代码如下:

# By Vamei

from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt

# Note the difference in "scale", which is std
rv1 = norm(loc=0, scale = 1)
rv2 = norm(loc=0, scale = 2)

x = np.linspace(-5, 5, 200)

plt.fill_between(x, rv1.pdf(x), y2=0.0, color="coral")
plt.fill_between(x, rv2.pdf(x), y2=0.0, color="green", alpha = 0.5)

plt.plot(x, rv1.pdf(x), color="red", label="N(0,1)")
plt.plot(x, rv2.pdf(x), color="blue", label="N(0,2)")

plt.legend()
plt.grid(True)

plt.xlim([-5, 5])
plt.ylim([-0.0, 0.5])

plt.title("normal distribution")
plt.xlabel("RV")
plt.ylabel("f(x)")

plt.show()

 

指数分布的方差

指数分布的表达式为

$$f(x) = \left\{ \begin{array}{rcl} \lambda e^{-\lambda x} & if & x \ge 0 \\ 0 & if & x < 0 \end{array} \right.$$

 

它的方差为

$$Var(X) = \frac{1}{\lambda^2}$$

 

如下图所示:

 

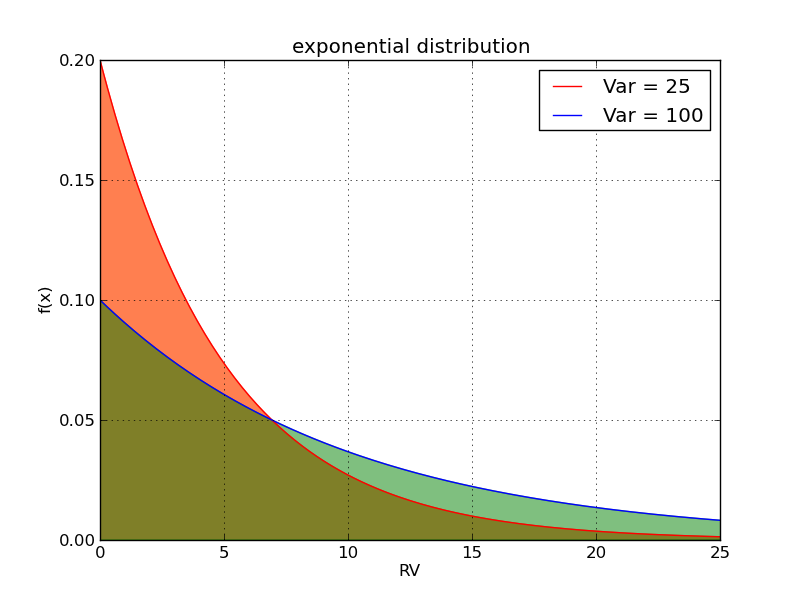
Chebyshev不等式

我们一直在强调，标准差(和方差)表示分布的离散程度。标准差越大，随机变量取值偏离平均值的可能性越大。如何定量的说明这一点呢？我们可以计算一个随机变量与期望偏离超过某个量的可能性。比如偏离超过2个标准差的可能性。即

$$P( | X - \mu | > 2\sigma)$$

这个概率依赖于分布本身的类型。比如正态分布[$N(0, 1)$]，这一概率即为x大于2，或者x小于-2的部分对应的曲线下面积：

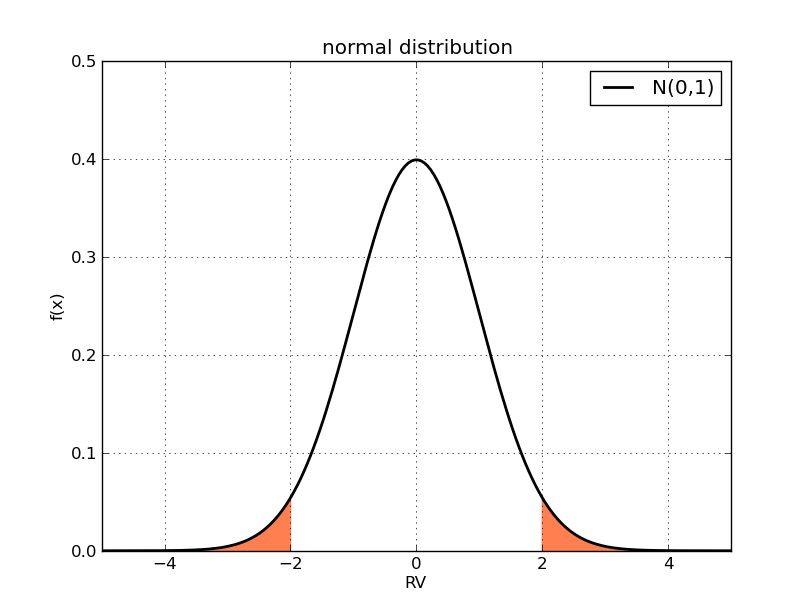
实际上，无论[$\mu$]和[$\sigma$]如何取值，对于正态分布来说，偏离期望超过两个标准差的概率都相同，约等于0.0455 (可以根据正态分布的表达式计算)。随机变量的取值有约95.545%的可能性落在正负两个标准差的区间内，即从-2到2。如果我们放大区间，比如正负三个标准差，这一概率超过99%。我们可以相当有把握的说，随机变量会落正负三个标准差之内。上面的论述并不依赖于标准差的具体值。这里可以看到标准差所衡量的“离散”的真正含义：如果取相同概率的极端值区间，比如上面的0.0455，标准差越大，该极端值区间距离中心值越远。

 

然而，上面的计算和表述依赖于分布的类型（正态分布）。如何将相似的方差含义套用在其它随机变量身上呢？

Chebyshev不等式让我们摆脱了对分布类型的依赖。它的叙述如下：

对于任意随机变量X，如果它的期望为[$\mu$]，方差为[$\sigma^2$]，那么对于任意[$t>0$]，

$$P( | X - \mu | > t) \le \frac{\sigma^2}{t}$$

 

无论X是什么分布，上述不等式成立。我们让[$t = 2\sigma$]，那么

$$P( | X - \mu | > 2\sigma) \le 0.25$$

也就是说，X的取值超过两个正负标准差的可能性最多为25%。换句话说，随机变量至少有75%的概率落在正负两个标准差的范围内。（显然这是最“坏”的情况下。正态分布显然不是”最坏“的）

 

绘图代码如下

from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt

# Note the difference in "scale", which is std
rv1 = norm(loc=0, scale = 1)

x1 = np.linspace(-5, -1, 100)
x2 = np.linspace(1, 5, 100)
x  = np.linspace(-5, 5, 200)
plt.fill_between(x1, rv1.pdf(x1), y2=0.0, color="coral")
plt.fill_between(x2, rv1.pdf(x2), y2=0.0, color="coral")
plt.plot(x, rv1.pdf(x), color="black", linewidth=2.0, label="N(0,1)")

plt.legend()
plt.grid(True)

plt.xlim([-5, 5])
plt.ylim([-0.0, 0.5])

plt.title("normal distribution")
plt.xlabel("RV")
plt.ylabel("f(x)")

plt.show()

 

 

总结

我们引入了一个新的分布描述量：方差。它用于表示分布的离散程度。

标准差为方差的平方根。

方差越大，“极端区间”偏离中心越远。

 

欢迎继续阅读“数据科学”系列文章