10月集训
感觉身为废物能整出来的题不多,所以说我可以只开一篇文章
9.29 [提高]
商店

通过推理,你可以找到选择\(i,j\)顺序的最优决策是选择\(\frac{a}{b+1}\)更大的
贪心啊贪心
\(\uarr\)错了
因为这个只是选择两个的顺序而不是选择的决策,你可能不选当中一个更优啊.
你要\(DP\)
然后是选择那些\(a=0\)的,这个部分也可以二分.
贴一份代码:
#include<bits/stdc++.h>
#define int long long
#define F(i0,i1,i2) for(int i0=(i1);i0<=(i2);++i0)
using namespace std;
inline int rd(){
int x=0,f=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return f?-x:x;
}
const int N=2e5+5,mod=1e9+7,inf= 0x3f3f3f3f;
struct Node{
int a,b;double val;
bool operator <(const Node &_)const{return val==_.val?b<_.b:val>_.val;}
}p[N];
int dp[N][100];
int n,T,ans,pos;
int c[N],k;
int get_num(int x){return lower_bound(c+1,c+1+n-k+1,x+0.5)-c-1;}
void Dp(){
F(i,0,n)F(j,0,min(n,30ll))dp[i][j]= inf;
dp[0][0]=0;
k=n+1;
F(i,1,n){
if(p[i].a==0){k=i;break;}
F(j,0,min(n,30ll)){
dp[i][j]=dp[i-1][j];
if(j)dp[i][j]=min((dp[i-1][j-1]+1)*(p[i].a+1)+p[i].b,dp[i-1][j]);
dp[i][j]=min(dp[i][j],inf);//这个很重要,防爆
}
}
F(i,k,n)c[i-k+1]=c[i-k]+1+p[i].b;
F(i,1,min(k-1,30ll)){
if(dp[k-1][i]>T)continue;
int x=get_num(T-dp[k-1][i]);
ans=max(ans,i+x);
}
cout<<ans<<'\n';
}
signed main(){
freopen("shop.in","r",stdin);
freopen("shop.out","w",stdout);
n=rd(),T=rd();
F(i,1,n){
p[i].a=rd(),p[i].b=rd();
p[i].val=(p[i].a)*1.0/(p[i].b+1);
}
sort(p+1,p+1+n);
Dp();
return 0;
}
下午茶


我们发现这个图建出来是一对一对环,这就基本上说明了做法
我们对于每一对环,可以同步处理\(i和P-i\),让他们对齐,然后做差,剩下来的就是糖果传递.
混蛋.
考试的时候不会糖果传递这不是必杀吗
#include<bits/stdc++.h>
#define int long long
#define F(i0,i1,i2) for(int i0=(i1);i0<=(i2);++i0)
using namespace std;
inline int rd(){
int x=0,f=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return f?-x:x;
}
const int N=2e6+5,mod=1e9+7;
int p,a[N],vis[N],v1[N],v2[N],c1,c2;
int s[N],c[N];
int solve(){
F(i,1,c1)s[i]=v1[i]-v2[i];
F(i,1,c1)c[i]=c[i-1]+s[i];
int x=(c1+1)>>1;
nth_element(c+1,c+x,c+1+c1);
int ans=0;
F(i,1,c1)ans+=abs(c[i]-c[x]);
return ans;
}
signed main(){
freopen("teatime.in","r",stdin);
freopen("teatime.out","w",stdout);
p=rd();
F(i,1,p-1){
a[i]=rd();
}
int ans=0;
F(i,1,p-1)if(!vis[i]){
int pos=i;
c1=c2=0;
while(!vis[pos]){
vis[pos]=1;
v1[++c1]=a[pos];
pos=pos*2%p;
}
pos=p-i;
while(!vis[pos]){
vis[pos]=1;
v2[++c2]=a[pos];
pos=pos*2%p;
}
ans+=solve();
}
cout<<ans<<'\n';
return 0;
}
模糊的字符串


相当于是查前驱情况是否相同,然后二分hash,可以用来出LSP
至于比较大小,这个要查第一个不一样的位置的字符在串中的是第几个出现的,这样就知道了
看起来能写,但是不好搞.
由于是单点修改,这个可持久化不涉及标签合并
#include<bits/stdc++.h>
#define int unsigned long long
#define F(i0,i1,i2) for(int i0=(i1);i0<=(i2);++i0)
using namespace std;
inline int rd(){
int x=0,f=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return f?-x:x;
}
const int N=2e5+5,base=19260817;
char _b;
int n,lim,a[N],pre[N];
int pw[N];
struct Seg{
struct Node{
int ls,rs;
int v;
}tr[N*10];
#define ls (tr[p].ls)
#define rs (tr[p].rs)
#define mid (l+r>>1)
int tot;
int rt[N];
void upd(int &p,int nx,int k,int l,int r){
tr[++tot]=tr[p];
p=tot;
if(l==r){
tr[p].v=k;
return ;
}
if(nx<=mid)upd(ls,nx,k,l,mid);
else upd(rs,nx,k,mid+1,r);
tr[p].v=tr[ls].v*pw[r-mid]+tr[rs].v;
}
int que_x(int p,int nx,int l,int r){
if(l==r)return tr[p].v;
if(nx<=mid)return que_x(ls,nx,l,mid);
else return que_x(rs,nx,mid+1,r);
}
int que(int p,int nl,int nr,int l,int r){
//cout<<l<<' '<<r<<'\n';
if(nl==l&&r==nr)return tr[p].v;
if(nr<=mid)return que(ls,nl,nr,l,mid);
else if(mid<nl)return que(rs,nl,nr,mid+1,r);
else return que(ls,nl,mid,l,mid)*pw[nr-mid]+que(rs,mid+1,nr,mid+1,r);
}
#undef ls
#undef rs
#undef mid
}hsh,chk;
#define mid (l+r>>1)
void solve(int l1,int r1,int l2,int r2){
int l=0,r=min(r1-l1+1,r2-l2+1)+1;
//int l=0,r=3;
while(r-l>1){
if(chk.que(chk.rt[l1],l1,l1+mid-1,1,n)==chk.que(chk.rt[l2],l2,l2+mid-1,1,n))l=mid;
else r=mid;
}
printf("%llu ",l);
int jud=(r1-l1==r2-l2? 0:(r1-l1<r2-l2? -1:1));
if(l<min(r1-l1+1,r2-l2+1)){
int c1=hsh.que_x(hsh.rt[l1],a[l1+l],1,lim)-hsh.que_x(hsh.rt[l1],a[l1],1,lim);
int c2=hsh.que_x(hsh.rt[l2],a[l2+l],1,lim)-hsh.que_x(hsh.rt[l2],a[l2],1,lim);
jud=(c1<c2? -1:1);
}
if(jud==-1) puts("a");
else if(jud==0) puts("same");
else puts("b");
}
char _c;
signed main(){
freopen("nuance.in","r",stdin);
freopen("nuance.out","w",stdout);
n=rd(),lim=rd();
pw[0]=1;
F(i,1,n)pw[i]=pw[i-1]*base;
F(i,1,n)a[i]=rd();
for(int i=n;i>=1;--i){
chk.rt[i]=chk.rt[i+1];
if(pre[a[i]])chk.upd(chk.rt[i],pre[a[i]],pre[a[i]]-i,1,n);
pre[a[i]]=i;
hsh.rt[i]=hsh.rt[i+1];
hsh.upd(hsh.rt[i],a[i],i,1,lim);
}
int m=rd();
F(i,1,m){
int l1=rd(),r1=rd(),l2=rd(),r2=rd();
solve(l1,r1,l2,r2);
}
return 0;
}
/*
9.30 [省选]
演唱会

首先,这个树的部分分很好搞,就是一个启发式就过了(我是废物这个都写挂了)
但是图呢?
我们发现对于点双,这个是可以缩起来的.
那就建圆方树吧.
发现我们只要认为方点不加距离,这个直接照样跑就是对的.
那么这里就有一份被卡了的启发式:
#include<bits/stdc++.h>
#define int long
#define F(i0,i1,i2) for(int i0=(i1);i0<=(i2);++i0)
using namespace std;
inline int rd() {
int x=0,f=0;
char ch=getchar();
while(!isdigit(ch)) {
if(ch=='-')f=1;
ch=getchar();
}
while(isdigit(ch)) {
x=x*10+ch-48;
ch=getchar();
}
return f?-x:x;
}
const int N=4e6+5,mod=1e9+7;
struct Id {
int v,nt;
} ef[N<<1],e[N<<1];
int p[N],id=1;
int pf[N],idf=1;
void addf(int x,int y) {
ef[++idf]= {y,pf[x]};
pf[x]=idf;
}
void add(int x,int y) {
e[++id]= {y,p[x]};
p[x]=id;
}
int n,m,L;
int tot;
int dfn[N],low[N],Tim;
int st[N],top;
void Tarjan(int x,int ffa) {
dfn[x]=low[x]=++Tim;
st[++top]=x;
for(int i=pf[x]; i; i=ef[i].nt) {
int v=ef[i].v;
if(v==ffa)continue;
if(!dfn[v]) {
Tarjan(v,x);
low[x]=min(low[x],low[v]);
if(low[v]>=dfn[x]) {
tot++;
add(x,tot);
add(tot,x);
while(top) {
int k=st[top--];
add(tot,k);
add(k,tot);
if(k==v)break;
}
}
} else low[x]=min(low[x],dfn[v]);
}
}
int dis[N],siz[N],son[N],in[N],inTim,afn[N];
void dfs1(int x,int ffa) {
dis[x]=dis[ffa]+(x<=n);
siz[x]=1;
in[x]=++inTim;
afn[inTim]=x;
for(int i=p[x]; i; i=e[i].nt) {
int v=e[i].v;if(v==ffa)continue;
dfs1(v,x);
siz[x]+=siz[v];
if(siz[son[x]]<siz[v])son[x]=v;
}
}
int cnt[N],ans[N];
void dfs2(int x,int ffa,int fl) {
for(int i=p[x]; i; i=e[i].nt) {
int v=e[i].v;
if(v==ffa||v==son[x])continue;
dfs2(v,x,0);
ans[x]+=ans[v];
}
if(son[x])dfs2(son[x],x,1),ans[x]+=ans[son[x]];
if(x<=n&&L+dis[ffa]<=n)ans[x]+=cnt[L+dis[ffa]];
if(x<=n)cnt[dis[x]]++;
for(int i=p[x]; i; i=e[i].nt) {
int v=e[i].v;
if(v==ffa||v==son[x])continue;
F(j,in[v],in[v]+siz[v]-1) {
int k=afn[j];
if(k<=n&&L+dis[x]+dis[ffa]-dis[k]>=0&&L+dis[x]+dis[ffa]-dis[k]<=n)
ans[x]+=cnt[L+dis[x]+dis[ffa]-dis[k]];
}
F(j,in[v],in[v]+siz[v]-1) {
int k=afn[j];
if(k<=n)cnt[dis[k]]++;
}
}
if(!fl)F(i,in[x],in[x]+siz[x]-1)cnt[dis[afn[i]]]=0;
}
signed main() {
freopen("sing.in", "r", stdin);
freopen("sing.out", "w", stdout);
n=rd(),m=rd(),L=rd();
F(i,1,m) {
int x=rd(),y=rd();
addf(x,y);
addf(y,x);
}
tot=n;
Tarjan(1,0);
dfs1(1,0);
dfs2(1,0,1);
cout<<ans[1]*2<<'\n';
return 0;
}
kernel_panic过了,我过不了纯属你妈的常数问题,受不了了
所以说我们只能开考虑复杂度更优秀的做法了.
可以发现我这里的桶只与深度有关,说明这个是可以长剖的,这下复杂度就是\(O(n)\)
这里是更正常的代码(天天学科技):
#include<bits/stdc++.h>
#define int long
#define F(i0,i1,i2) for(int i0=(i1);i0<=(i2);++i0)
using namespace std;
inline int rd() {
int x = 0, f = 0;
char ch = getchar();
while(!isdigit(ch)) {
if(ch == '-')f = 1;
ch = getchar();
}
while(isdigit(ch)) {
x = x * 10 + ch - 48;
ch = getchar();
}
return f ? -x : x;
}
const int N = 4e6 + 5, mod = 1e9 + 7;
struct Id {
int v, nt;
} ef[N << 1], e[N << 1];
int p[N], id = 1;
int pf[N], idf = 1;
void addf(int x, int y) {
ef[++idf] = {y, pf[x]};
pf[x] = idf;
}
void add(int x, int y) {
e[++id] = {y, p[x]};
p[x] = id;
}
int n, m, L;
int tot;
int dfn[N], low[N], Tim;
int st[N], top;
void Tarjan(int x, int ffa) {
dfn[x] = low[x] = ++Tim;
st[++top] = x;
for(int i = pf[x]; i; i = ef[i].nt) {
int v = ef[i].v;
if(v == ffa)continue;
if(!dfn[v]) {
Tarjan(v, x);
low[x] = min(low[x], low[v]);
if(low[v] >= dfn[x]) {
tot++;
add(x, tot);
add(tot, x);
while(top) {
int k = st[top--];
add(tot, k);
add(k, tot);
if(k == v)break;
}
}
} else low[x] = min(low[x], dfn[v]);
}
}
int dep[N], son[N];
void dfs1(int x, int ffa) {
for(int i = p[x]; i; i = e[i].nt) {
int v = e[i].v;
if(v == ffa)continue;
dfs1(v, x);
if(dep[son[x]] < dep[v])son[x] = v;
}
dep[x] = dep[son[x]] + 1;
}
int buf[N];
int ans;
int *f[N],*now=buf;
void dfs2(int x,int ffa){
f[x][0]=(x<=n);
if(son[x]){
f[son[x]]=f[x]+1;
dfs2(son[x],x);
if(L-1<=dep[son[x]]){
ans+=f[son[x]][L-1]*(x<=n);
}//can change
}
for(int i=p[x];i;i=e[i].nt){
int v=e[i].v;
if(v==ffa||v==son[x])continue;
f[v]=now;
now+=dep[v];
dfs2(v,x);
F(j,1,dep[v]){
if(j<=L&&L-j<=dep[x])ans+=f[v][j-1]*f[x][L-j];
}
F(j,1,dep[v])f[x][j]+=f[v][j-1];
}
}
signed main() {
freopen("sing.in", "r", stdin);
freopen("sing.out", "w", stdout);
n = rd(), m = rd(), L = rd();
L=(L-1)*2;
F(i, 1, m) {
int x = rd(), y = rd();
addf(x, y);
addf(y, x);
}
tot = n;
Tarjan(1, 0);
dfs1(1, 0);
f[1]=now;
now+=dep[1];
dfs2(1, 0);
cout << ans *2<< '\n';
return 0;
}
Graph
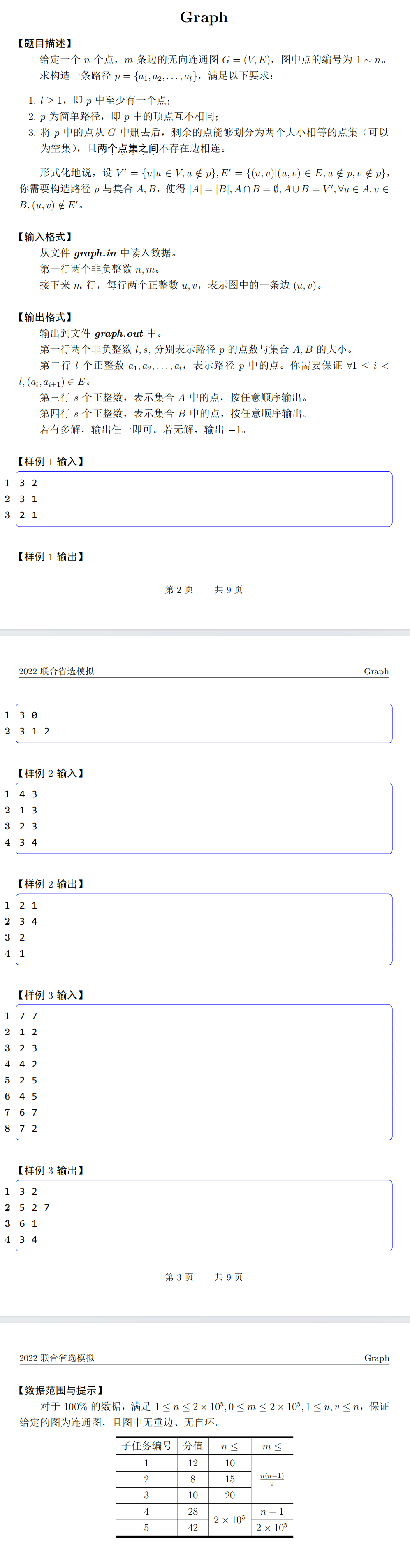
你妈的构造
主要是开始题都读错了,\(A,B\)中的点根本不用联通.
那么我们有一种很好的构造:
从根(1)开始,然后开始深搜,入栈就是入\(p\)退\(B\),回溯就是出\(p\),入\(A\),很好我们发现这样\(|B|-|A|\)是连续变化的,肯定会有一刻相等,看来这个做法对于树没有任何问题;
我们再发现一个性质,只有横叉边会导致我们这个构造的答案错误,但是很遗憾,我们的dfs生成树是不存在横叉边的,那么就是说,对于一个图直接深搜就行了.
混蛋.
#include<bits/stdc++.h>
#define int long long
#define F(i0,i1,i2) for(int i0=(i1);i0<=(i2);++i0)
using namespace std;
inline int rd(){
int x=0,f=0;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return f?-x:x;
}
const int N=1e6+5,mod=1e9+7;
struct Id{int v,nt;}e[N<<1];
int p[N],id=1;
void add(int x,int y){e[++id]={y,p[x]};p[x]=id;}
int n,m;
int na;
int a[N];
int st[N],top;
int vis[N];
int b[N];
void check(){
if(na==n-na-top){
cout<<top<<' '<<na<<'\n';
while(top){
b[st[top]]=1;
cout<<st[top--]<<" ";
}cout<<'\n';
while(na){
b[a[na]]=1;
cout<<a[na--]<<' ';
}cout<<'\n';
F(i,1,n)if(!b[i])cout<<i<<' ';cout<<'\n';
exit(0);
}
}
void dfs(int x,int ffa){
vis[x]=1;
st[++top]=x;
check();
for(int i=p[x];i;i=e[i].nt){
int v=e[i].v;if(vis[v])continue;
dfs(v,x);
}
a[++na]=x;
top--;
check();
}
signed main(){
freopen("graph.in", "r", stdin);
freopen("graph.out", "w", stdout);
n=rd(),m=rd();
F(i,1,m){
int x=rd(),y=rd();
add(x,y);
add(y,x);
}
dfs(1,0);
return 0;
}
/*
4 3
1 3
2 3
3 4
*/
Counting

虽然说写不了,但是思路还是值得留意的.
首先我们考虑无m限制的,发现这个就是卡特兰数.
有上界的情况呢?我们考虑一个反射的思想.
就是说,如果这条线触碰到了\(m\)上界,那么意味着把线以\(m\)为轴反射后能到达\(2*m\)点
那么我们直接容一下,减去这种方案就行了.
但是这里有上界有下届.
设触碰上界为\(a\),下届为\(b\)
那么就有\(a,b,ab,ba,aba,bab,abab,baba...\)
发现这个方案相减是个容斥,系数就是\(-1^{方案长度(对于同种触碰合并)}\)
每改变一次就反射一次,越来越远.
最后再加上空位置填上不动,乘上组合,这题就做完了
多项式和GF,写个锤子



 浙公网安备 33010602011771号
浙公网安备 33010602011771号