深度学习的概述

深度学习的应用场景

图像应用

• 大规模(大数据量)图片识别(聚类/分类)，如人脸识别，车牌识别，OCR等
• 以图搜图，图像分割
• 目标检测，如自动驾驶的行人检测，安防系统的异常人群检测

自然语言处理

• 语音识别，语音合成，自动分词，句法分析，语法纠错，关键词提取，文本分类/聚类，文本自动摘要， 信息检索（ES,Solr）
• 知识图谱，机器翻译，人机对话，机器写作
• 推荐系统，高考机器人
• 信息抽取，网络爬虫，情感分析，问答系统

数据挖掘，风控系统，广告系统等

神经网络的起源

机器学习回顾

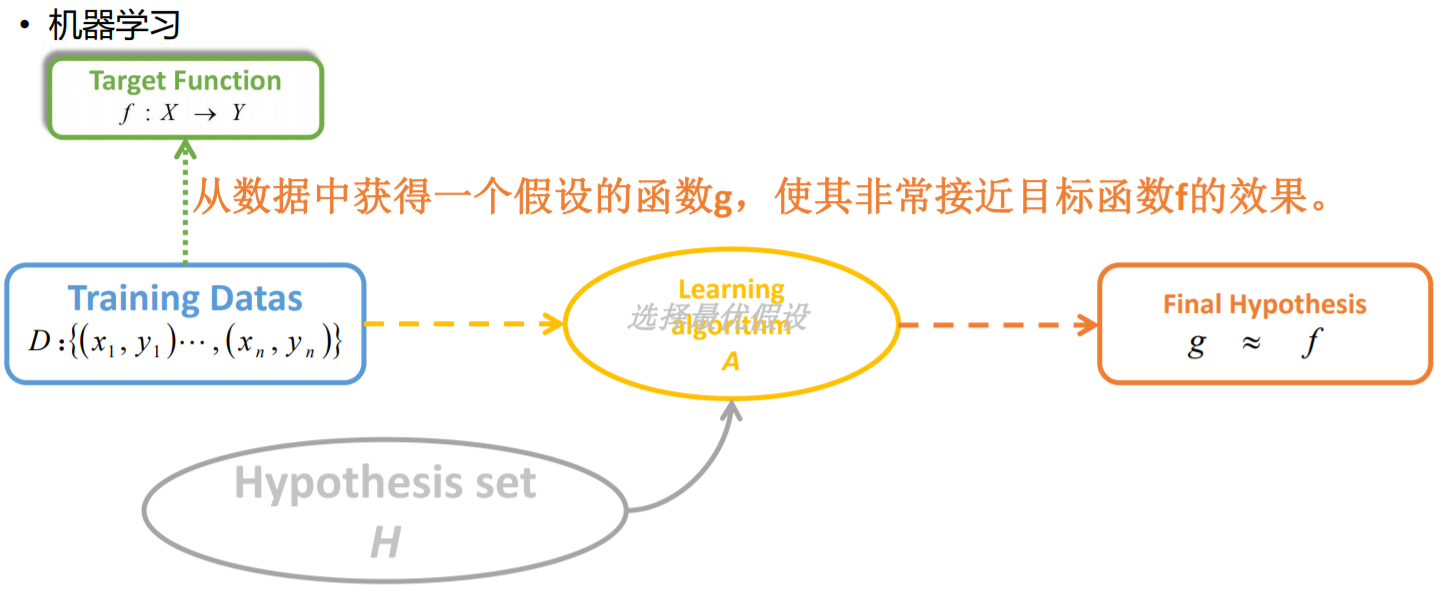
神经网络来源之人的思考

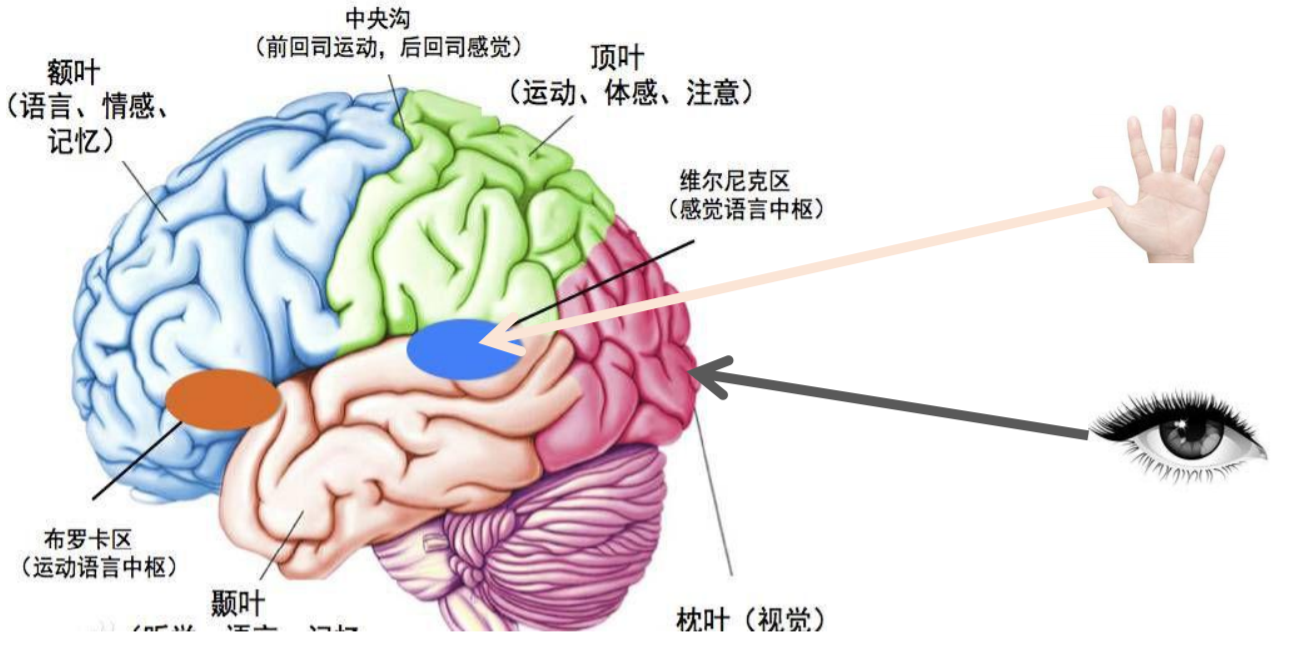
大脑是由处理信息的神经元细胞和连接神经元的细胞进行信息传递的突触构成的。树突 (Dendrites)从一个神经元接受电信号，信号在细胞核(Cell Body)处理后，然后通过轴突(Axon) 将处理的信号传递给下一个神经元。

一个神经元可以看作是将一个或多个输入处理成一个输出的计算单元。

通过多个神经元的传递，最终大脑会得到这个信息，并可以对这个信息给出一个合适的反馈。

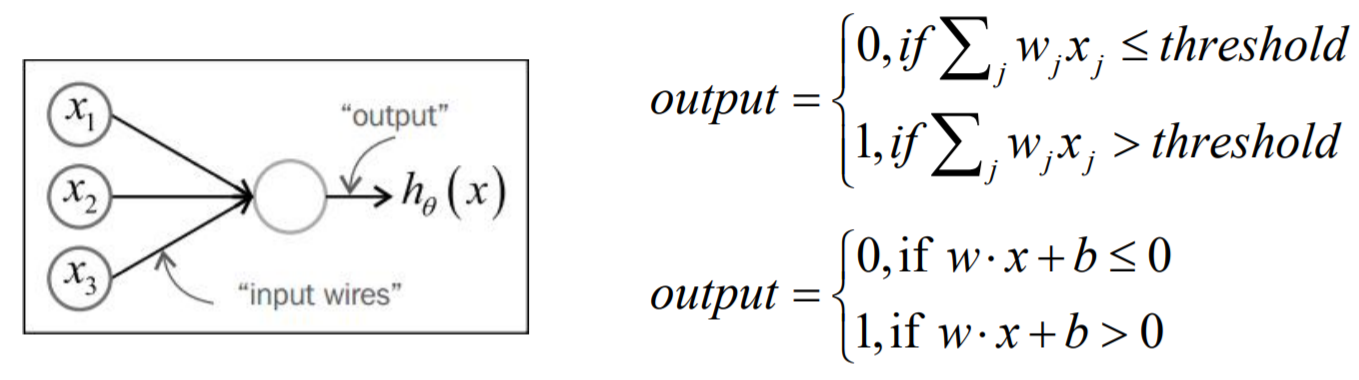
感知器是一种模拟人的神经元的一种算法模型，是一种研究单个训练样本的二元分类器， 是SVM和人工神经网络(ANN, Artificial Neural Networks)的基础。

一个感知器接受几个二进制的输入，并产生一个二进制的输出，通常的表达方式如下：

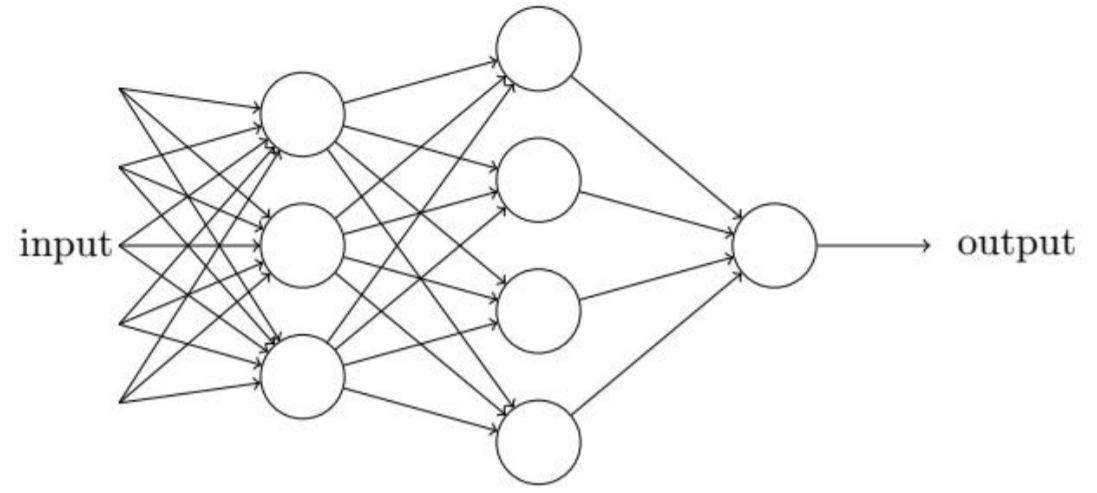
多层感知器(人工神经网络)

将多个感知器进行组合，我们就可以得到一个多层感知器的网络结构，网络中的每一个节 点我们叫做神经元。

感知器神经元直观理解之逻辑与

import tensorflow as tf
import os
import tensorflow_datasets as tfds
import matplotlib.pyplot as plt
import numpy as np
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'

w1 = tf.Variable([[2.],[2.]],dtype=tf.float32)
b1 = tf.Variable(initial_value=-3,dtype=tf.float32)

x = np.array([[0,0],[0,1],[1,0],[1,1]]).astype(dtype=np.float)
y = np.array([0,0,0,1]).reshape(-1,1).astype(dtype=np.float)

X = tf.compat.v1.placeholder(dtype=tf.float32)
Y = tf.compat.v1.placeholder(dtype=tf.float32)
#函数输出
pre = tf.add(tf.matmul(X,w1),b1)

#构建损失函数
err = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels=Y,logits=pre))

#优化损失
op = tf.compat.v1.train.AdamOptimizer(learning_rate=0.005).minimize(err)

with tf.compat.v1.Session() as sess:
    sess.run(tf.compat.v1.global_variables_initializer())
    while True:
        e, _ = sess.run([err,op],feed_dict={X:x,Y:y})
        print(e)
        if e < 0.05:
            w1,b1 = sess.run([w1,b1])
            print(w1)
            print(b1)
            temp_x = (-b1-w1[1,0])/w1[0,0]
            line_x = np.linspace(np.min([temp_x,1.]),np.max([temp_x,1.]),10)
            line_y = (-b1-line_x*w1[0,0])/w1[1,0]
            plt.scatter(x[:3,0],x[:3,1],s=300)
            plt.scatter(x[3,0],x[3,1],marker='*',s=300)
            plt.plot(line_x,line_y)
            plt.show()
            break

感知器神经元直观理解之逻辑或

import tensorflow as tf
import os
import tensorflow_datasets as tfds
import matplotlib.pyplot as plt
import numpy as np
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'

w1 = tf.Variable([[2.],[2.]],dtype=tf.float32)
b1 = tf.Variable(initial_value=-3,dtype=tf.float32)

x = np.array([[0,0],[0,1],[1,0],[1,1]]).astype(dtype=np.float)
y = np.array([0,1,1,1]).reshape(-1,1).astype(dtype=np.float)

X = tf.compat.v1.placeholder(dtype=tf.float32)
Y = tf.compat.v1.placeholder(dtype=tf.float32)
#函数输出
pre = tf.add(tf.matmul(X,w1),b1)

#构建损失函数
err = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(labels=Y,logits=pre))

#优化损失
op = tf.compat.v1.train.AdamOptimizer(learning_rate=0.005).minimize(err)

with tf.compat.v1.Session() as sess:
    sess.run(tf.compat.v1.global_variables_initializer())
    while True:
        e, _ = sess.run([err,op],feed_dict={X:x,Y:y})
        print(e)
        if e < 0.05:
            w1,b1 = sess.run([w1,b1])
            print(w1)
            print(b1)
            temp_x = (-b1-w1[1,0])/w1[0,0]
            line_x = np.linspace(np.min([temp_x,1.]),np.max([temp_x,1.]),10)
            line_y = (-b1-line_x*w1[0,0])/w1[1,0]
            plt.scatter(x[1:,0],x[1:,1],s=300)
            plt.scatter(x[0,0],x[0,1],marker='*',s=300)
            plt.plot(line_x,line_y)
            plt.show()
            break

感知器神经元直观理解之非线性可分

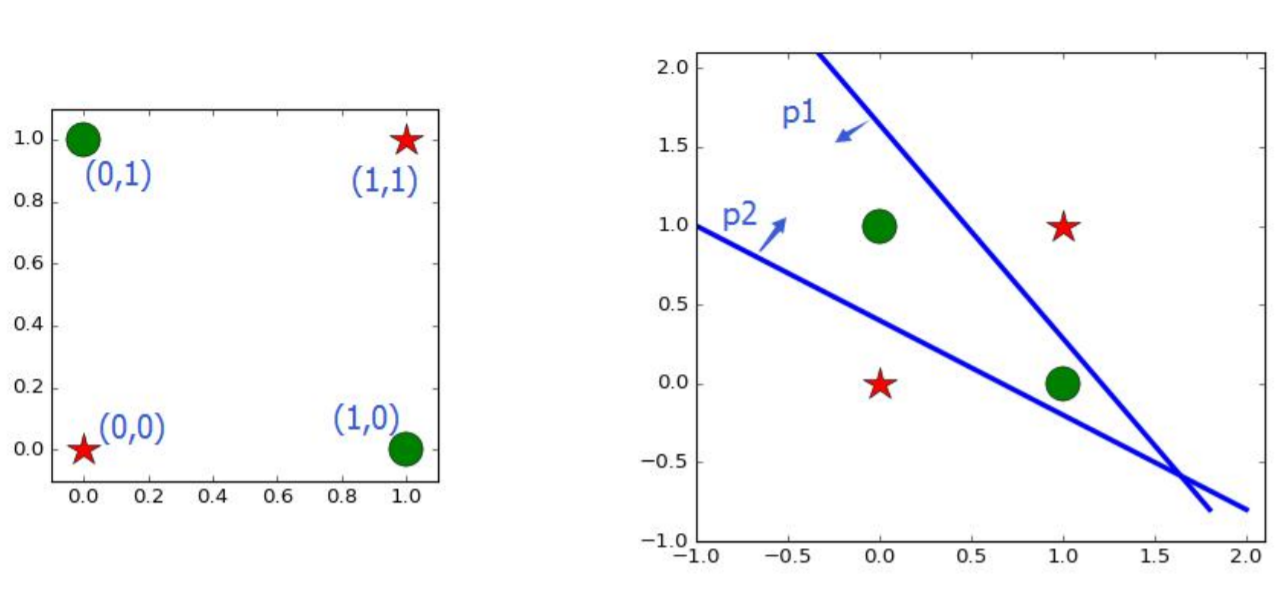
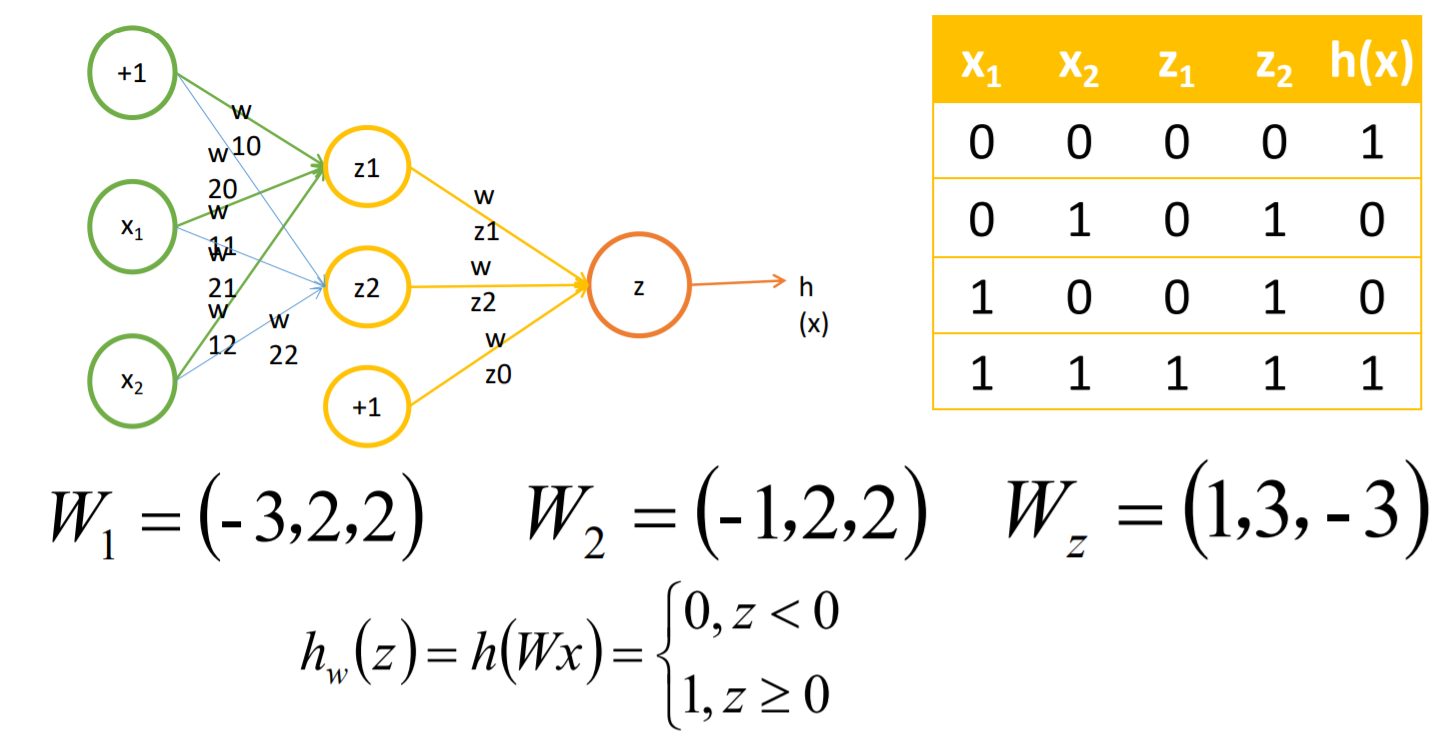
感知器网络理解以及S型神经元

针对感知器网络的这种很难学习的问题，引入S型神经元来代替感知器，从而解决这个问 题。

从感知器模型中，我们可以将单个神经元的计算过程看成下列两个步骤：

• 先计算权重w和输入值x以及偏置项b之间的线性结果值z：z=wx+b
• 然后对结果值z进行一个数据的sign函数(变种)转换，得到一个离散的0/1值: y=int((sign(z)+1)/2)

在S型神经元中，和感知器神经元的区别在于：

• 对于结果值z的转换，采用的不是sign函数进行转换，是采用平滑类型的函数进行转换，让输出的 结果值y最终是一个连续的，S型神经元转指使用的是sigmoid函数。

神经网络来源之“神经元”

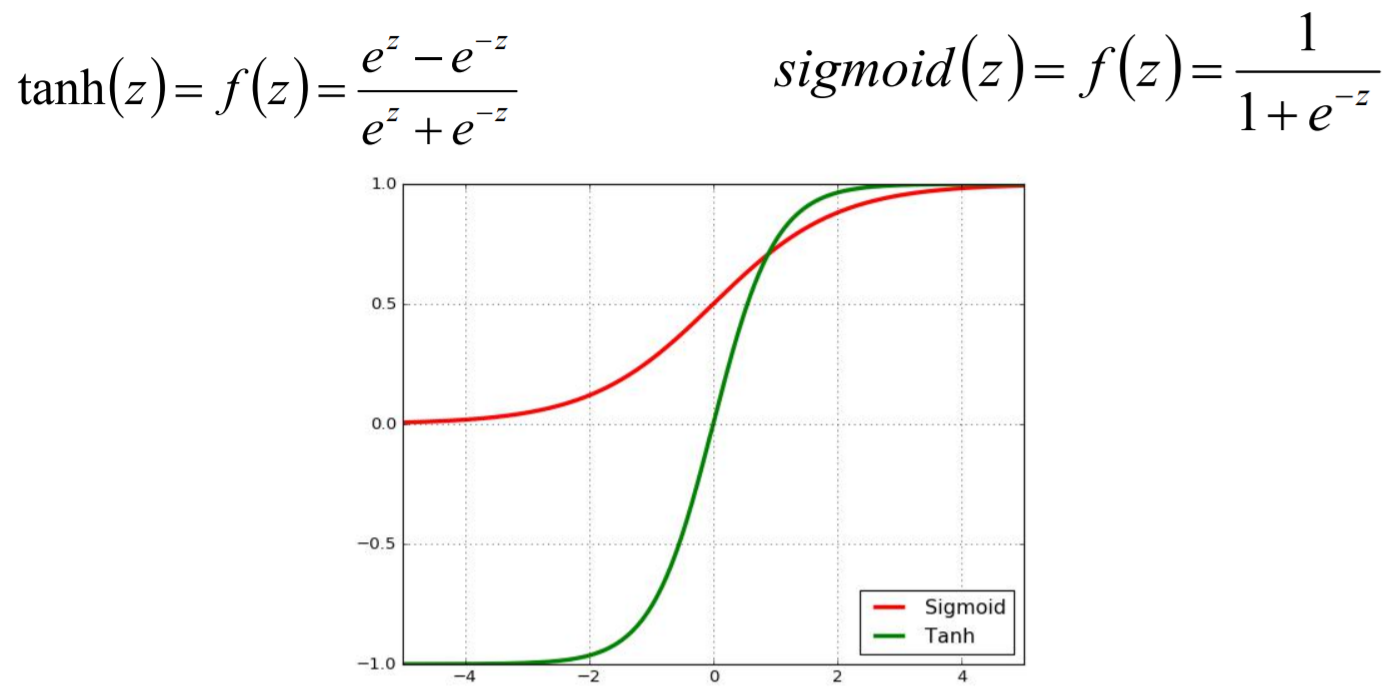
激活函数

激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数，那么该网络仅能 够表达线性映射，此时即便有再多的隐藏层，其整个网络跟单层神经网络也是等价的。因 此也可以认为，只有加入了激活函数之后，深度神经网络才具备了分层的非线性映射学习 能力。 激活函数的主要特性是：可微性、单调性、输出值的范围；

常见的激活函数：

• Sign函数
• Sigmoid函数
• Tanh函数
• ReLU函数
• P-ReLU函数
• Leaky-ReLU函数
• ELU函数
• Maxout函数等

神经网络的基本结构

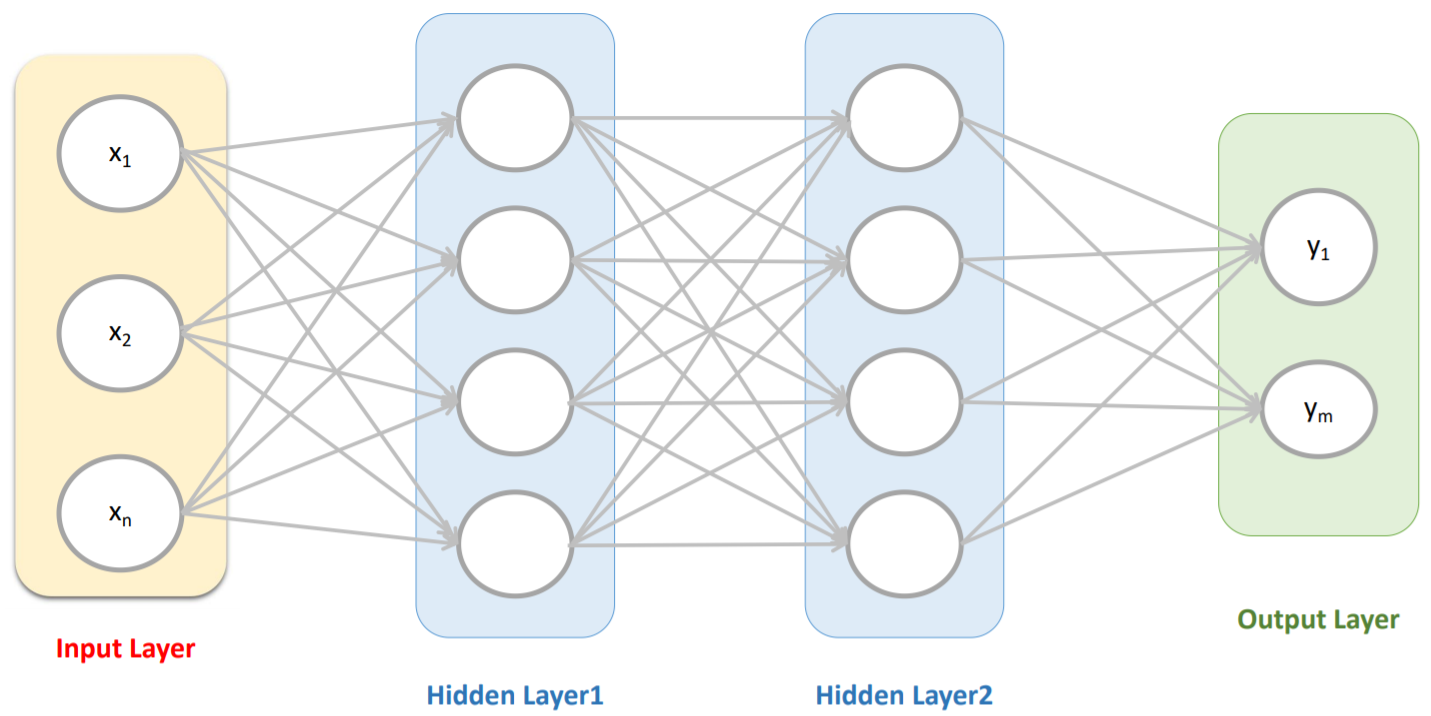
神经网络主要由三个组成部分，第一个是架构（architecture）或称为拓扑结构 （topology），描述神经元的层次与连接神经元的结构。第二个组成部分是神经网络使 用的激励/激活函数。第三个组成部分是找出最优权重值的学习算法。

神经网络主要分为两种类型，前馈神经网络(Feedforward Neural Networks)是最常用 的神经网络类型，一般定义为有向无环图，信号只能沿着最终输出的那个方向传播。另外 一个是反馈神经网络(Feedback Neural Networks)，也称为递归神经网络(Recurent Neural Networks)，也就是网络中环。

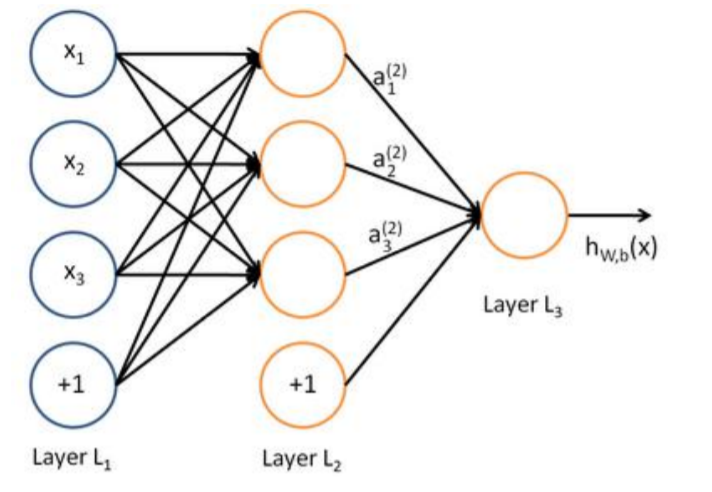
神经网络之浅层神经网络

添加少量隐层的神经网络就叫做浅层神经网络；也叫作传统神经网络，一般为2隐层的神 经网络(超过两隐层的话，效果会差很多)。

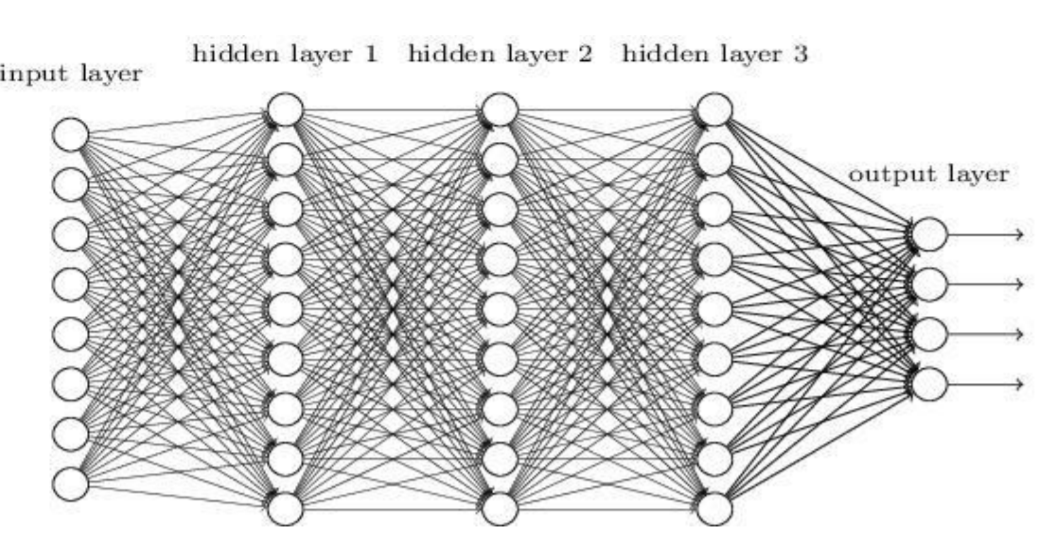
神经网络之深度神经网络

增多中间层(隐层)的神经网络就叫做深度神经网络(DNN)；可以认为深度学习是神经网络 的一个发展。

神经网络之非线性可分

对线性分类器的与和或的组合可以完成非线性可分的问题；即通过多层的神经网络中加入激活函数的方式可以解决非线性可分的问题。

神经网络之过拟合

理论上来讲，单隐层的神经网络可以逼近任何连续函数（只要隐层的神经元个数足够的多 <一个神经元将数据集分为两类>。

虽然从数学表达上来讲，效果一样，但是在网络工程效果中，多隐层的神经网络效果要比 单隐层的神经网络效果好。

对于一些分类的问题来讲，三层的神经网络效果优于两层的神经网络，但是如果把层次不 断增加(4,5,6,7....)，对于最终的效果不会产生太大的变化。

提升隐层层数或者神经元个数，神经网络的“容量”会变大，那么空间表达能力会变强， （模型的预测能力），从而有可能导致过拟合的问题。

对于视频/图片识别等问题，传统的神经网络(全连接神经网络)不太适合。

BP神经网络

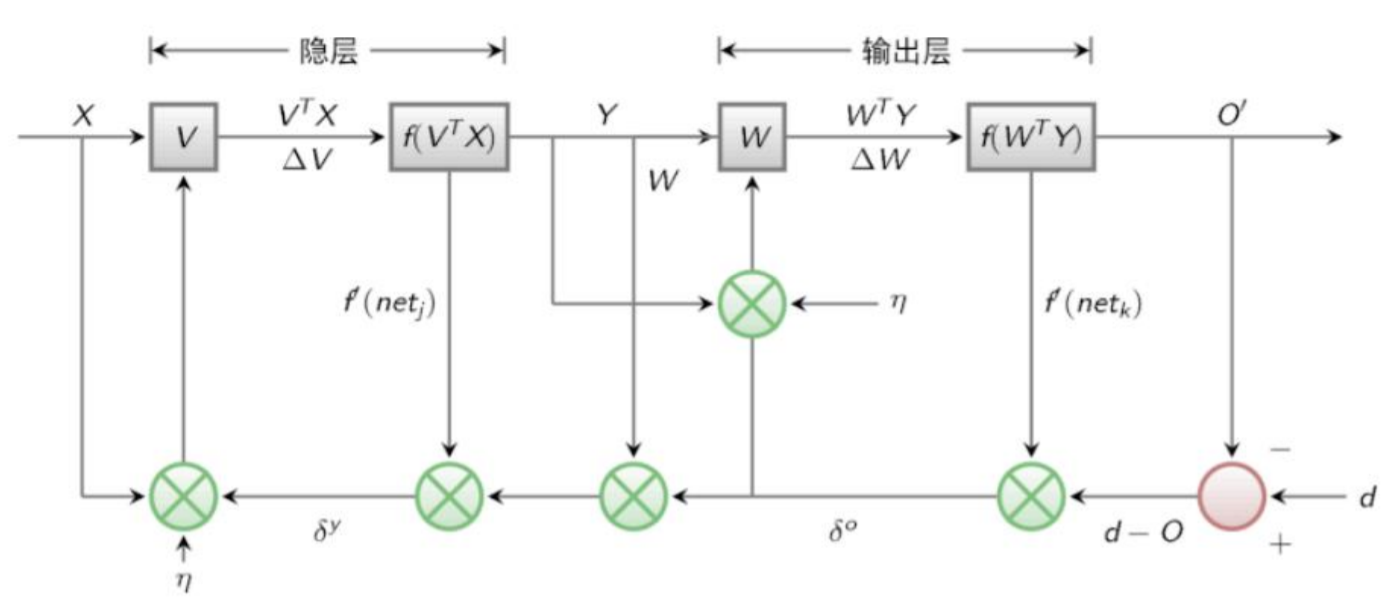
BP算法也叫做δ算法

以三层的感知器为例（假定现在隐层和输出层均存在相同类型的激活函数）

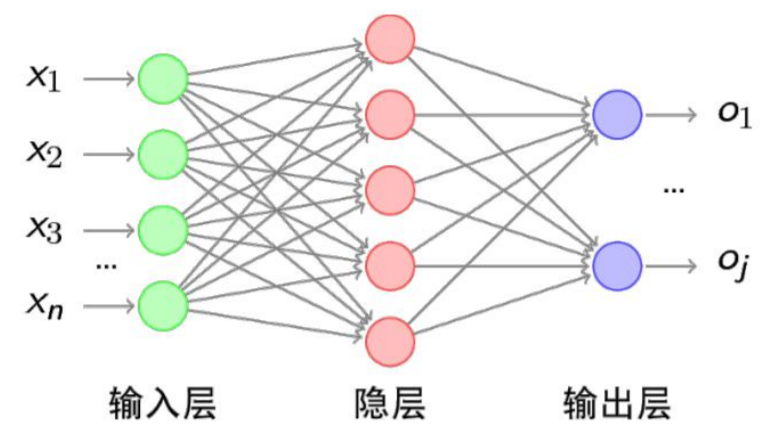
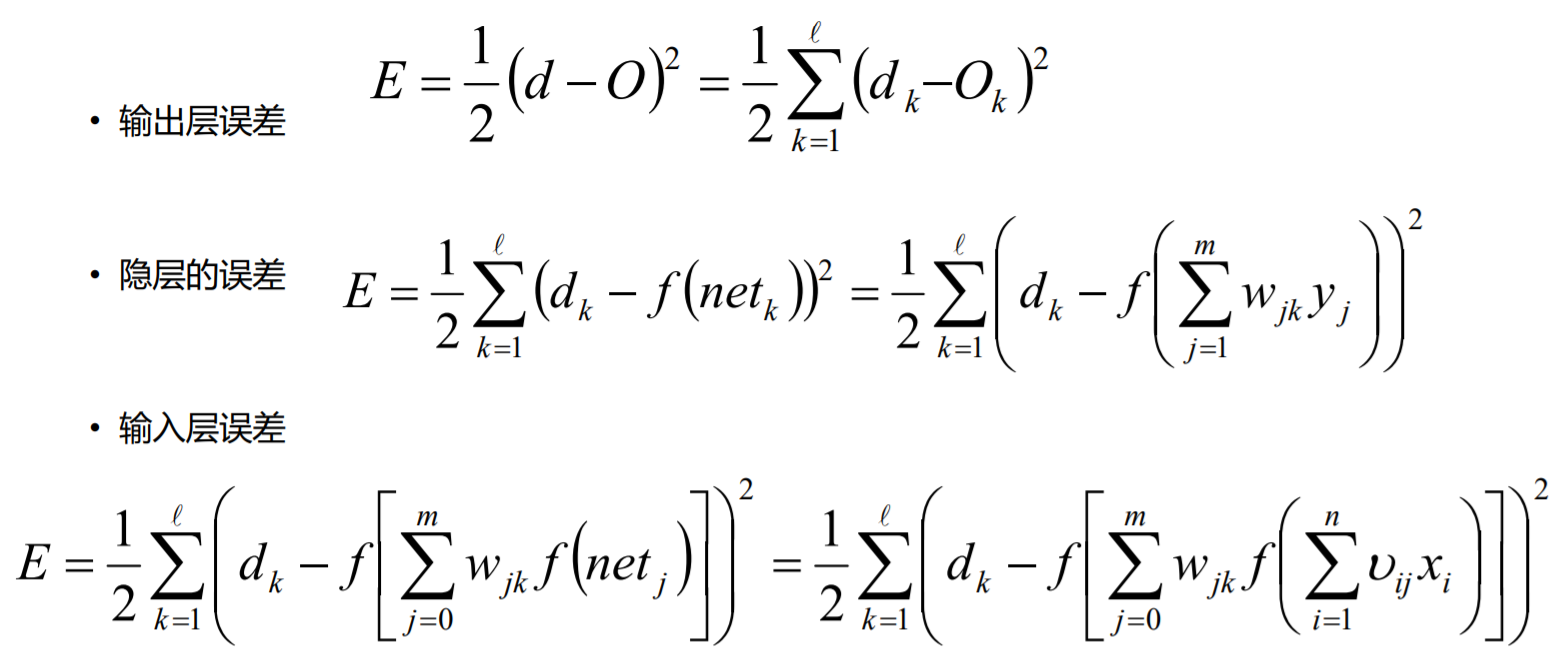
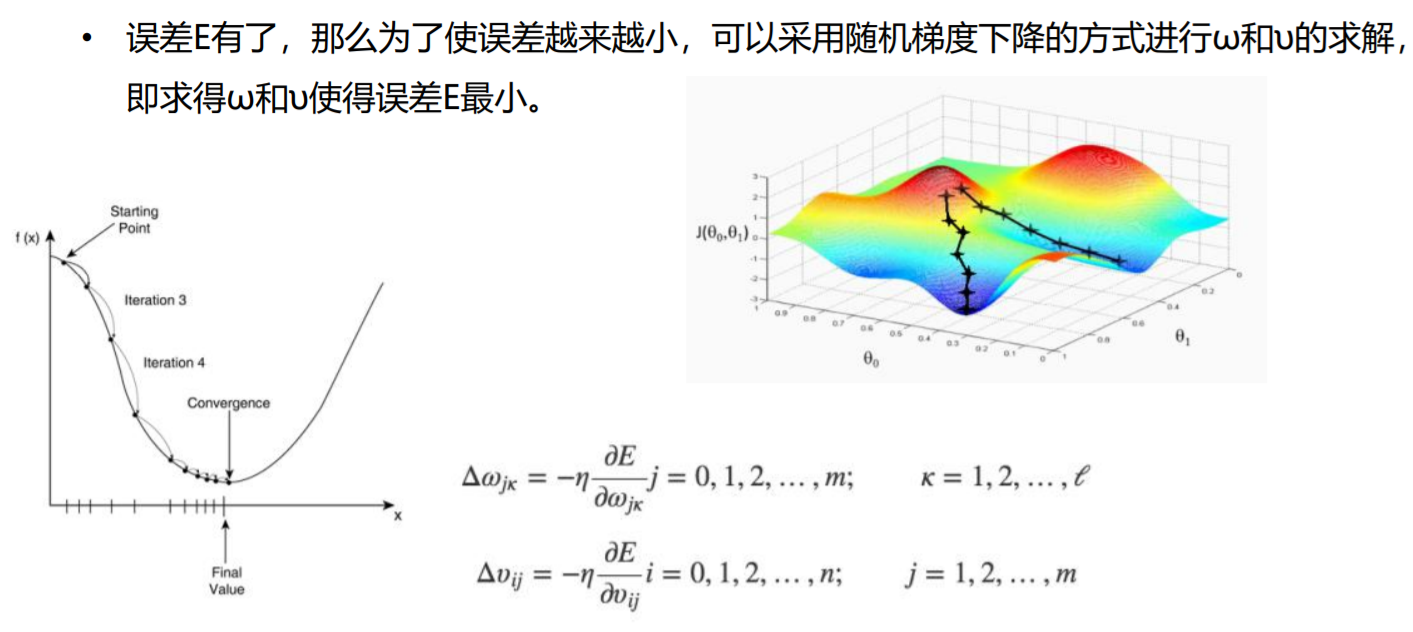
神经网络之SGD

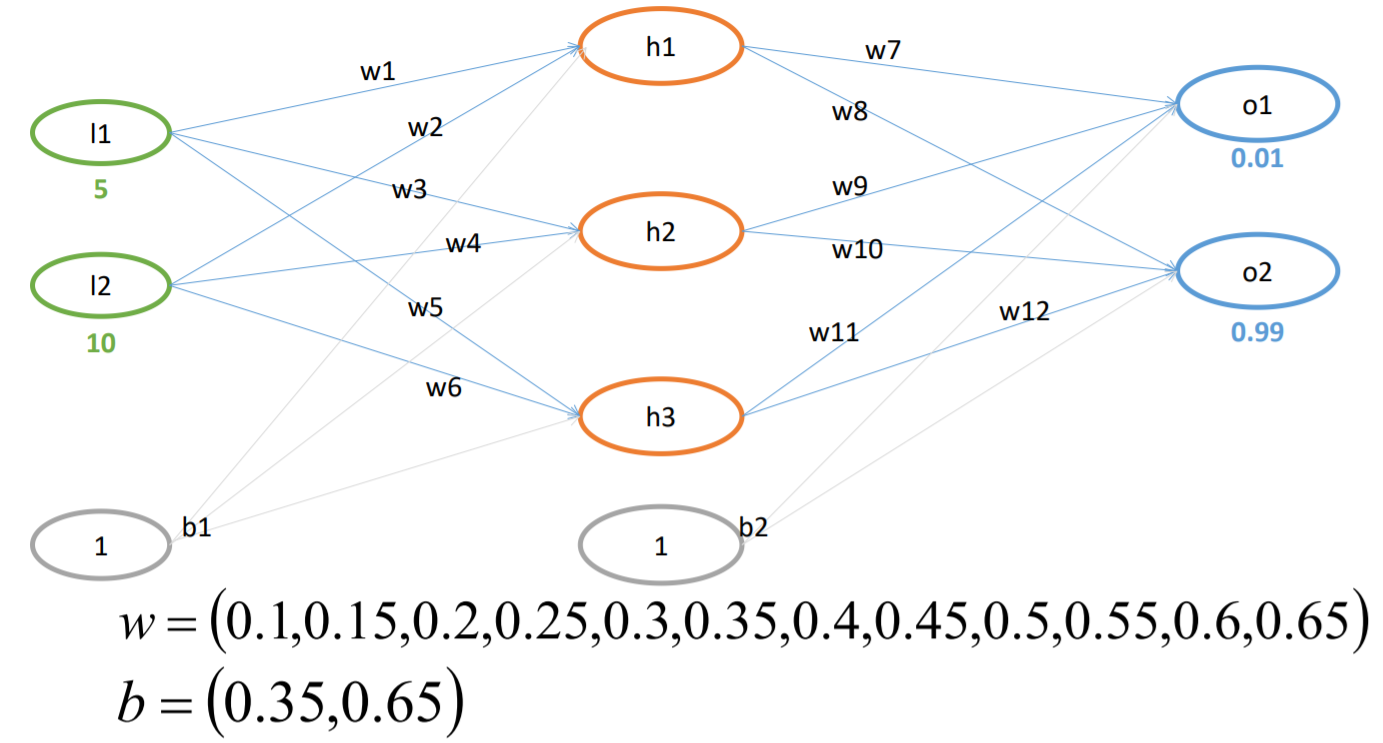
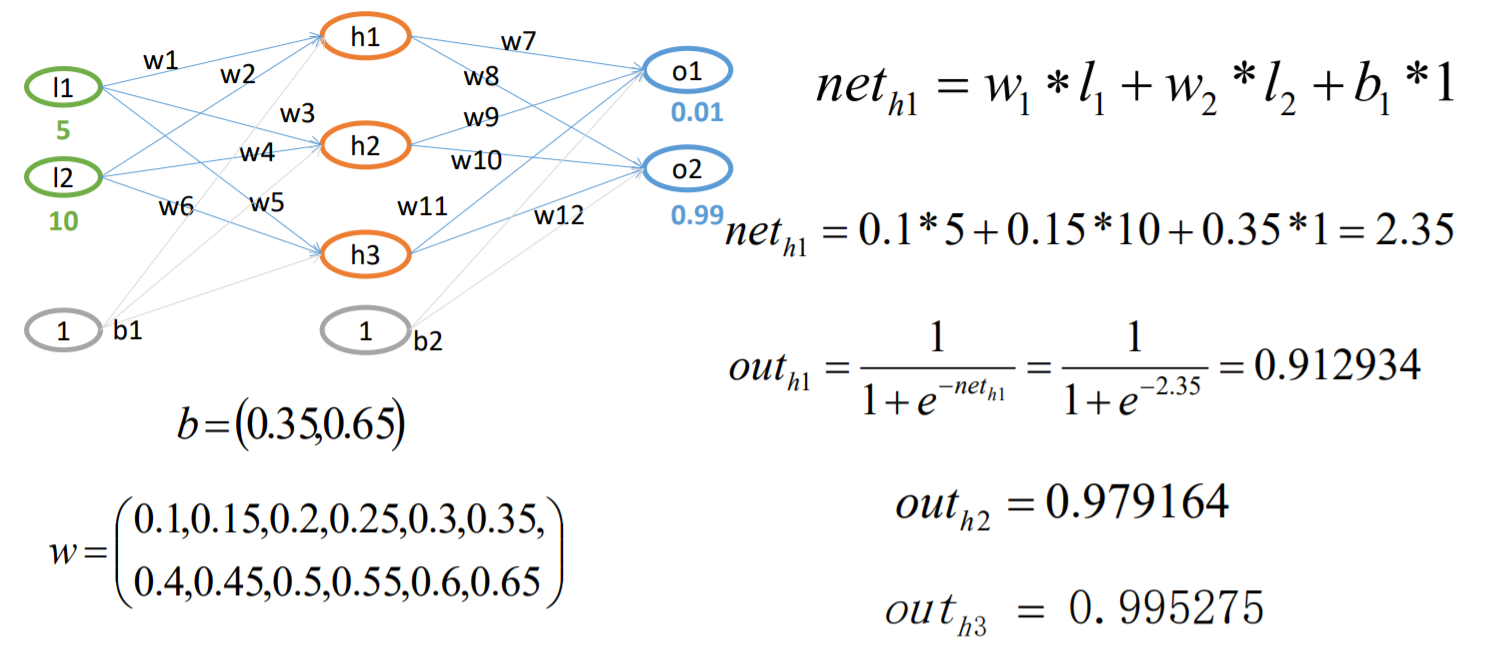
BP算法例子-FP过程

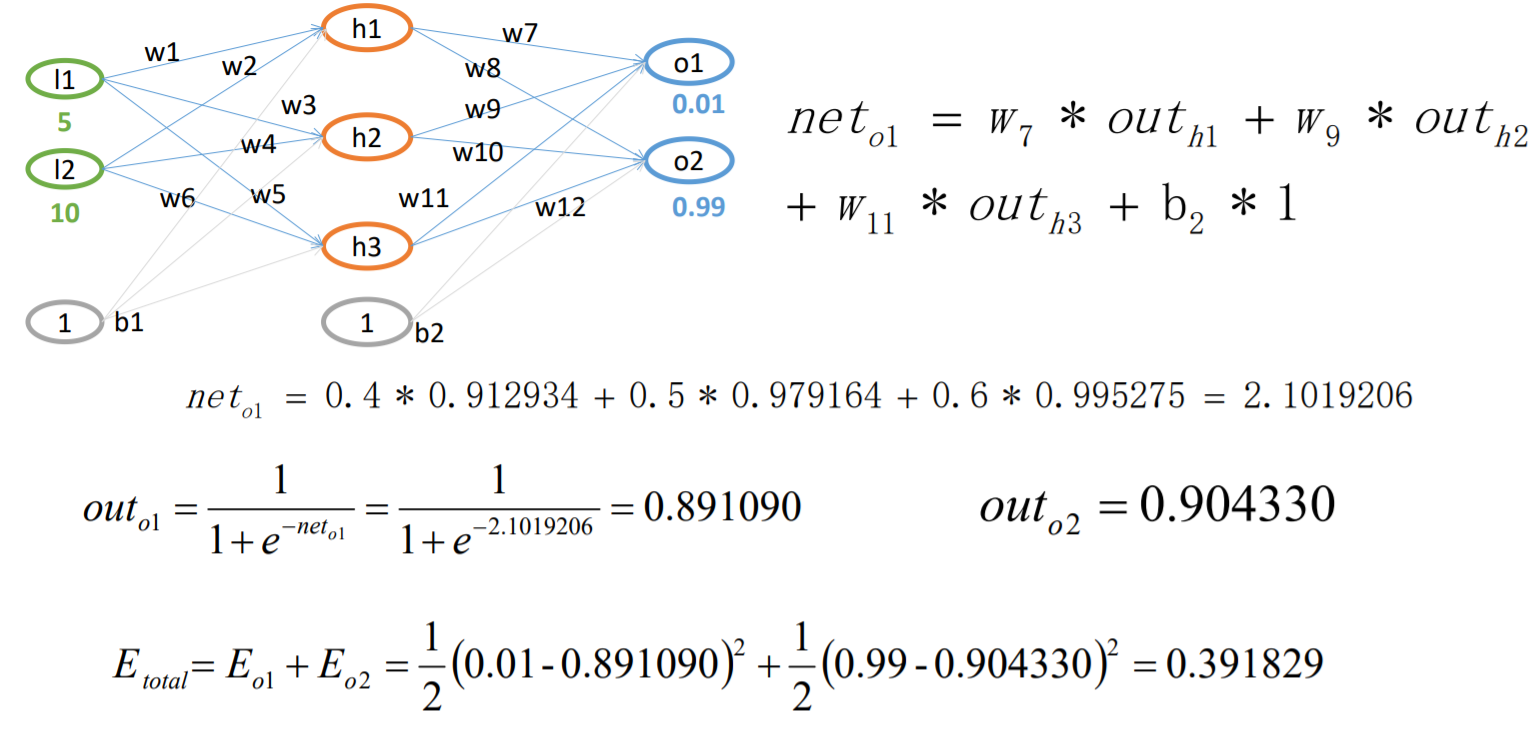
BP算法例子-BP过程(W7)

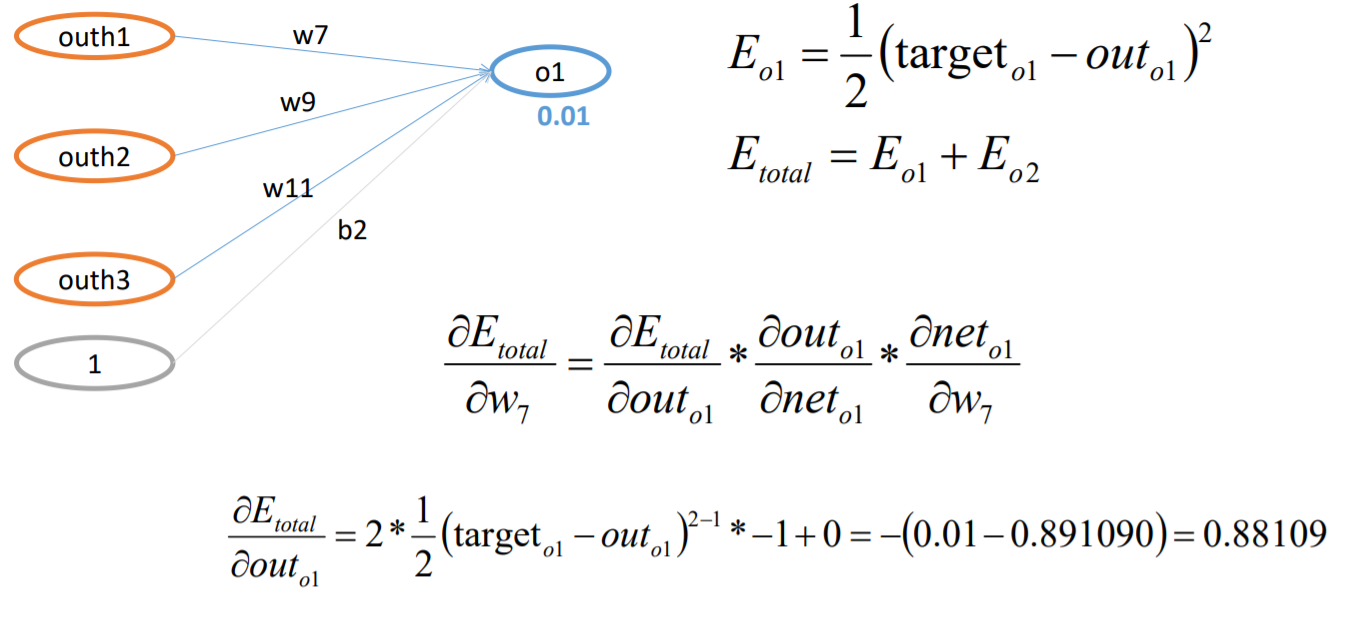
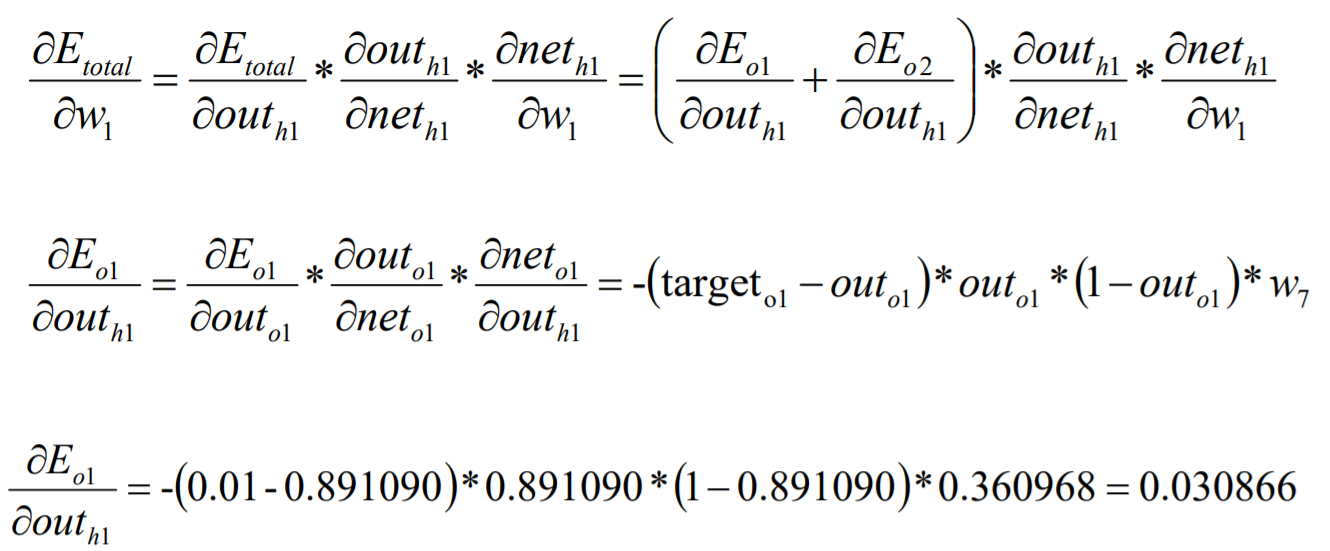
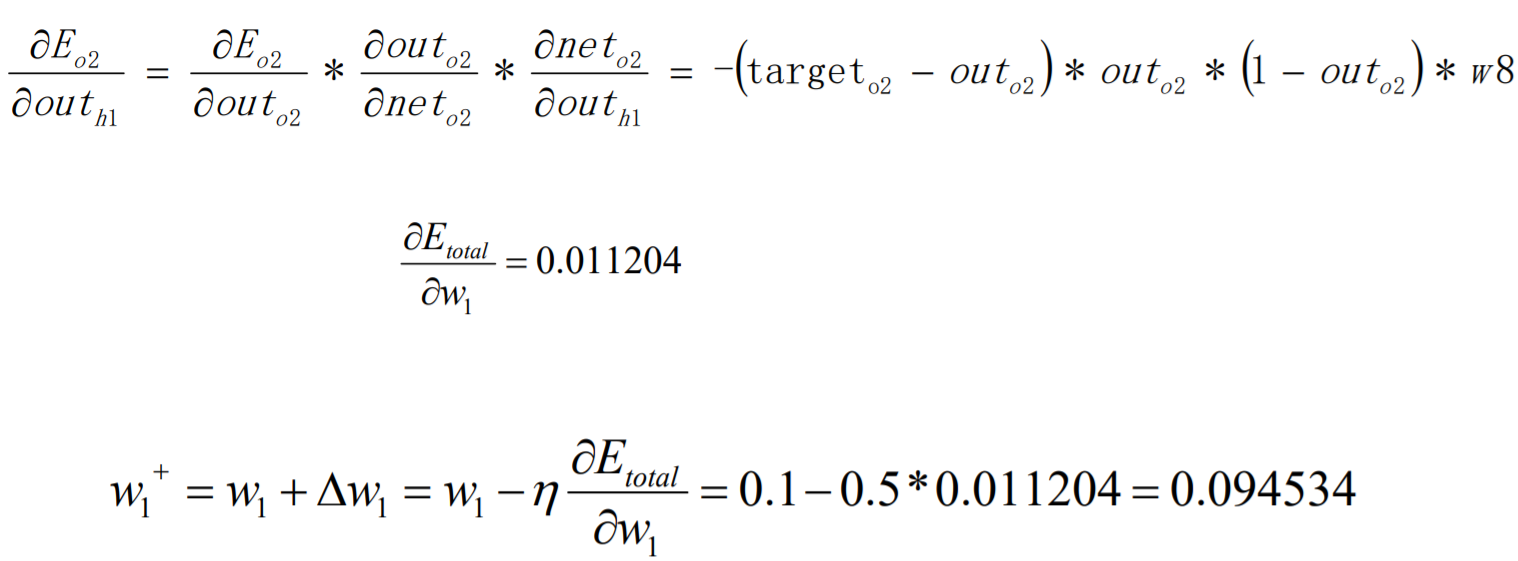
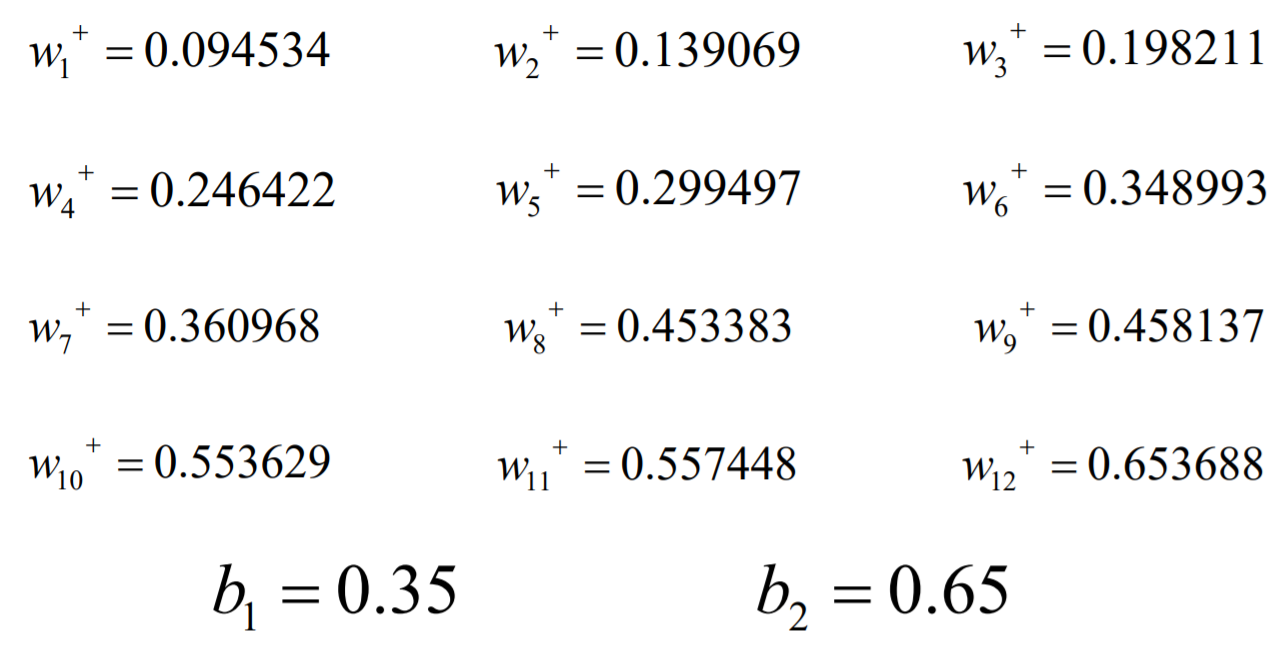
import numpy as np
# I=[5,10]
# O=[0.01,0.99]

I = [[5, 10], [10, 5], [11, 4], [4, 12], [9, 6], [3, 9]]
O = [[0, 1], [1, 0], [1, 0], [0, 1], [1, 0], [0, 1]]
W=[0.1+i*0.05 for i in range(12)]
B1=np.array([[1.,1.,1.]])
B2=np.array([[1.,1.]])
# sigmoid
def sigmoid(z):
    return 1/(1+np.exp(-z))

# fp
def train(W,B1,B2):
    input=np.array(I).reshape([-1,2])
    target=np.array(O).reshape([-1,2])
    #[0.1,0.15,0.2,0.25,0.3,0.35]
    weights_input_to_hidden=np.array(W[0:6]).reshape([3,2]).T#shape(2,3)
    weights_hidden_out=np.array(W[6:]).reshape([3,2])
    for i in range(100000):
        #输入层到隐层
        hidden_input=np.dot(input,weights_input_to_hidden).T# (1,3)=>(3,1)
        # 隐层激活
        hidden_out=sigmoid(hidden_input+B1.T).T#(3,1)+(3,1)=>(3,1)=>(3,1)=>(1,3)
        # 隐层到输出层
        final_input=np.dot(hidden_out,weights_hidden_out).T
        final_out=sigmoid(final_input+B2.T).T

        # 损失计算 真实减去预测值
        out_errors=target-final_out#*** 根据实际的损失做调整

        # bp
        # 隐层损失
        # e_total对那一层的权重求导的结果*中间的系数（hidden-out*（1-hidden-out)）
        # hidden_errors=(np.dot(-out_errors,weights_input_to_hidden)*(hidden_out*(1-hidden_out))).T# [3,1]
        # print(hidden_errors)

        # # 变换量
        # weights_hidden_out+=out_errors*hidden_out.T*0.5
        # weights_input_to_hidden+=(hidden_errors*input*0.5).T
        # W=weights_hidden_out.to_list().T.extend(weights_input_to_hidden.to_list())
        chain_rule = out_errors*final_out*(1-final_out) #(batch_zise,2)

        batch_size = input.shape[0]
        dw2=0.5*np.dot(hidden_out.T,chain_rule)
        db2=0.5*np.dot(np.ones((batch_size,1)).T,chain_rule)# 前面的1代表batch_size，后面的1代表b的系数
        delat1 = np.dot(chain_rule,weights_hidden_out.T) * (1 - hidden_out) * hidden_out #(batch_zise,3)
        dw1=0.5*np.dot(input.T,delat1)
        db1=0.5*np.dot(np.ones((batch_size,1)).T,delat1)#前面的1代表batch_size，后面的1代表b的系数
        weights_hidden_out+=dw2
        weights_input_to_hidden+=dw1

        B1+=db1
        B2+=db2

    # 还原W
    return sum(sum(out_errors)**2),weights_input_to_hidden,weights_hidden_out,B1,B2


e,w,w2,B1,B2=train(W,B1,B2)
result = sigmoid(np.dot(sigmoid(np.dot(I, w))+B1, w2)+B2)
res = np.zeros(result.shape)
for i,k in enumerate(zip(result,np.argmax(result,axis=1))):
    res[i][k[1]] = 1

print(res)

def my_bp():
    import numpy as np

    I = [[5, 10], [10, 5], [11, 4], [4, 12], [9, 6], [3, 9]]
    O = [[0, 1], [1, 0], [1, 0], [0, 1], [1, 0], [0, 1]]
    W = [0.1 + i * 0.05 for i in range(12)]

    # sigmoid
    def sigmoid(z):
        return 1 / (1 + np.exp(-z))

    input = np.array(I).reshape([-1, 2])
    target = np.array(O).reshape([-1, 2])
    # [0.1,0.15,0.2,0.25,0.3,0.35]
    weights_input_to_hidden = np.array(W[0:6]).reshape([3, 2]).T  # shape(2,3)
    weights_hidden_to_out = np.array(W[6:]).reshape([3, 2])

    def train(input, weights_input_to_hidden, weights_hidden_to_out, target, n_iter, intercept=False):
        if intercept:
            m_one = np.ones((input.shape[0], 1))
            input = np.hstack((input, m_one))
            weights_bias_input2hidden = np.vstack(
                (weights_input_to_hidden, np.ones((1, weights_input_to_hidden.shape[-1]))))
            weights_bias_hidden2out = np.vstack((weights_hidden_to_out, np.ones((1, weights_hidden_to_out.shape[-1]))))
            for i in range(n_iter):
                # 输入层到隐层
                hidden_input = np.dot(input, weights_bias_input2hidden).T  # (batch_size,3)=>(3,batch_size)
                # 隐层激活
                hidden_out = sigmoid(hidden_input).T  # (3,batch_size)+(3,batch_size)=>(3,batch_size)=>(3,batch_size)=>(batch_size,3)
                hidden_as_input = np.hstack((hidden_out, m_one))

                # 隐层到输出层
                final_input = np.dot(hidden_as_input, weights_bias_hidden2out).T
                final_out = sigmoid(final_input).T

                # 损失计算 真实减去预测值
                out_errors = target - final_out  # *** 根据实际的损失做调整
                out_gd = out_errors * final_out * (1 - final_out)
                dw2 = np.dot(hidden_as_input.T, out_gd)
                dw1 = np.dot(input.T, np.dot(out_gd, weights_hidden_to_out.T) * hidden_out * (
                        1 - hidden_out))

                weights_bias_input2hidden += 0.5 * dw1
                weights_bias_hidden2out += 0.5 * dw2
                weights_hidden_to_out = weights_bias_hidden2out[:-1]

            weights_input_to_hidden = weights_bias_input2hidden[:-1]
            bias_input_to_hidden = weights_bias_input2hidden[-1]
            weights_hidden_to_out = weights_bias_hidden2out[:-1]
            bias_hidden_to_out = weights_bias_hidden2out[-1]

            return weights_input_to_hidden, bias_input_to_hidden, weights_hidden_to_out, bias_hidden_to_out
        else:
            for i in range(n_iter):
                # 输入层到隐层
                hidden_input = np.dot(input, weights_input_to_hidden).T  # (batch_size,3)=>(3,batch_size)
                # 隐层激活
                hidden_out = sigmoid(hidden_input).T
                # 隐层到输出层
                final_input = np.dot(hidden_out, weights_hidden_to_out).T
                final_out = sigmoid(final_input).T

                # 损失计算 真实减去预测值
                out_errors = target - final_out  # *** 根据实际的损失做调整
                out_gd = out_errors * final_out * (1 - final_out)

                dw2 = np.dot(0.5 * hidden_out.T, out_gd)
                dw1 = np.dot(0.5 * input.T, np.dot(out_gd, weights_hidden_to_out.T) * hidden_out * (
                        1 - hidden_out))

                weights_input_to_hidden += dw1
                weights_hidden_to_out += dw2

            return weights_input_to_hidden, weights_hidden_to_out

    # weights_input_to_hidden, weights_hidden_to_out = train(input, weights_input_to_hidden, weights_hidden_to_out,
    #                                                        target, 100000, )
    # print(weights_input_to_hidden)
    # print(weights_hidden_to_out)
    #
    # print(sigmoid(np.dot(sigmoid(np.dot(I, weights_input_to_hidden)), weights_hidden_to_out)))

    weights_input_to_hidden,b1,weights_hidden_to_out,b2 = train(input,weights_input_to_hidden,weights_hidden_to_out,target,100000,True)
    print(weights_input_to_hidden)
    print(weights_hidden_to_out)
    print(b1)
    print(b2)
    print(sigmoid(np.dot(sigmoid(np.dot(I,weights_input_to_hidden)+b1),weights_hidden_to_out)+b2))
# my_bp()

RBF神经网络

RBF神经网络通常只有三层，即输入层、中间层和输出层。其中中间层主要计算输入x和样 本矢量c（记忆样本）之间的欧式距离的Radial Basis Function (RBF) 的值，输出层对其做 一个线性的组合。

 

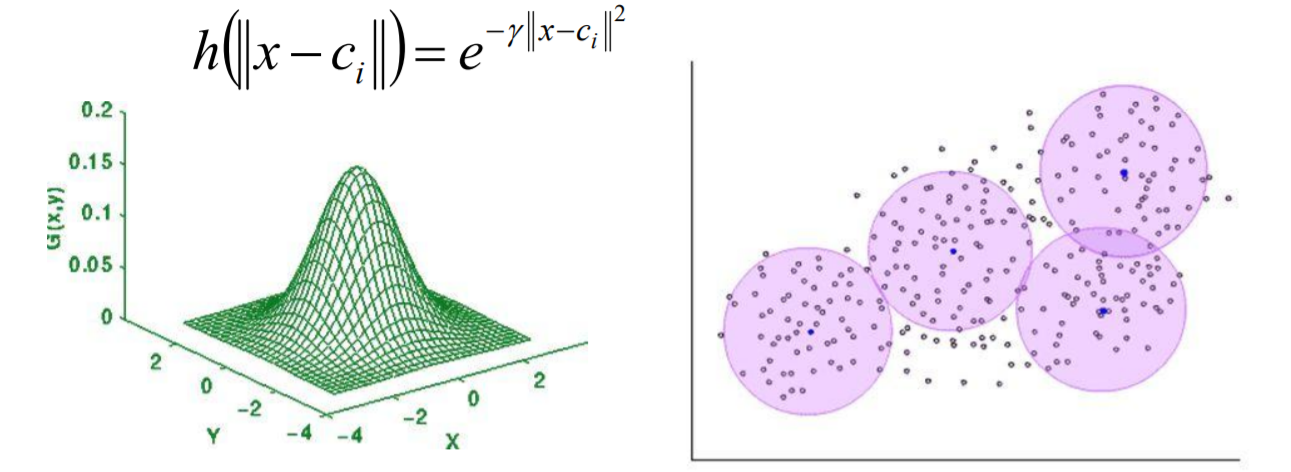
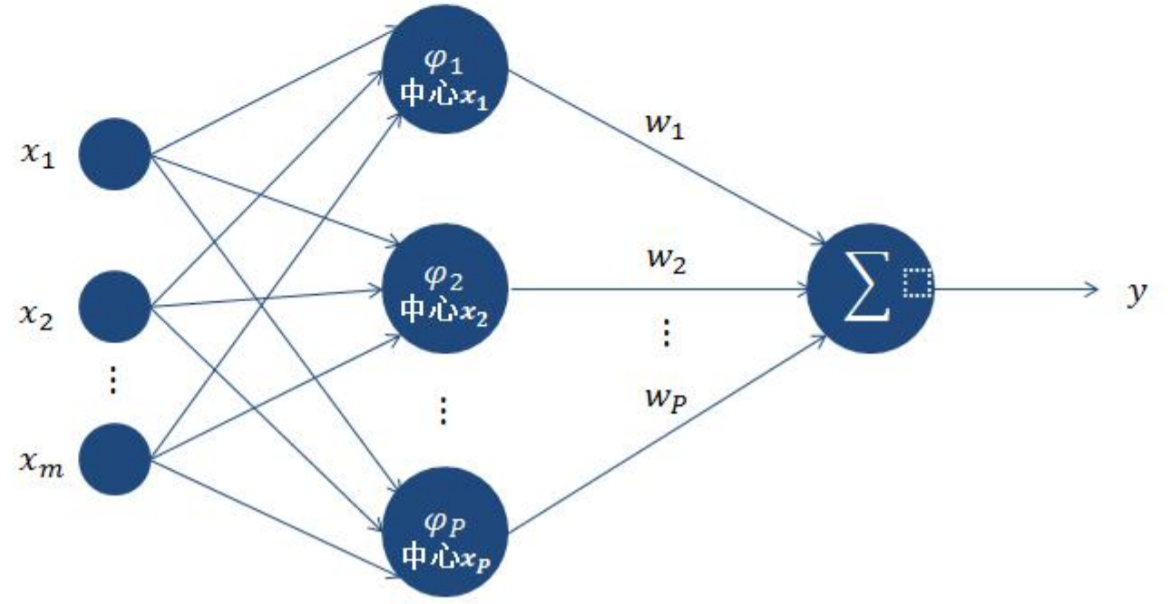
RBF神经网络的训练可以分为两个阶段：

• 第一阶段为无监督学习，从样本数据中选择记忆样本/中心点；可以使用聚类算法，也可以选择随 机给定的方式。
• 第二阶段为监督学习，主要计算样本经过RBF转换后，和输出之间的关系/权重；可以使用BP算法 计算、也可以使用简单的数学公式计算。

RBF网络能够逼近任意非线性的函数(因为使用的是一个局部的激活函数。在中心点附近有 最大的反应；越接近中心点则反应最大，远离反应成指数递减；就相当于每个神经元都对 应不同的感知域)。

可以处理系统内难以解析的规律性，具有很好的泛化能力，并且具有较快的学习速度。

有很快的学习收敛速度，已成功应用于非线性函数逼近、时间序列分析、数据分类、模式 识别、信息处理、图像处理、系统建模、控制和故障诊断等。

当网络的一个或多个可调参数（权值或阈值）对任何一个输出都有影响时，这样的网络称 为全局逼近网络。由于对于每次输入，网络上的每一个权值都要调整，从而导致全局逼近 网络的学习速度很慢，比如BP网络。

如果对于输入空间的某个局部区域只有少数几个连接权值影响输出，则该网络称为局部逼 近网络，比如RBF网络。

BP神经网络(使用Sigmoid激活函数)是全局逼近；RBF神经网络(使用径向基函数作为激活 函数)是局部逼近；

相同点：

• RBF神经网络中对于权重的求解也可以使用BP算法求解。

不同点：

• 中间神经元类型不同(RBF:径向基函数；BP:Sigmoid函数)
• 网络层次数量不同(RBF:3层；BP:不限制)
• 运行速度的区别(RBF:快；BP:慢)

神经网络之DNN问题

一般来讲，可以通过增加神经元和网络层次来提升神经网络的学习能力，使其得到的模型 更加能够符合数据的分布场景；但是实际应用场景中，神经网络的层次一般情况不会太大， 因为太深的层次有可能产生一些求解的问题。

在DNN的求解中有可能存在两个问题：梯度消失和梯度爆炸；我们在求解梯度的时候会使 用到链式求导法则，实际上就是一系列的连乘，如果每一层都小于1的话，则梯度越往前乘 越小，导致梯度消失，而如果连乘的数字在每层都是大于1的，则梯度越往前乘越大，导致梯度爆炸。

练习

使用Python实现BP神经网络实现对公路客运量即公路货运量预测案例

import pandas as pd
#人数(单位：万人),.
population=[20.55,22.44,25.37,27.13,29.45,30.10,30.96,34.06,36.42,38.09,39.13,39.99,41.93,44.59,47.30,52.89,55.73,56.76,59.17,60.63]
#机动车数(单位：万辆)
vehicle=[0.6,0.75,0.85,0.9,1.05,1.35,1.45,1.6,1.7,1.85,2.15,2.2,2.25,2.35,2.5,2.6,2.7,2.85,2.95,3.1]
#公路面积(单位：万平方公里)
roadarea=[0.09,0.11,0.11,0.14,0.20,0.23,0.23,0.32,0.32,0.34,0.36,0.36,0.38,0.49,0.56,0.59,0.59,0.67,0.69,0.79]

# [20,2]
#公路客运量(单位：万人)
passengertraffic=[5126,6217,7730,9145,10460,11387,12353,15750,18304,19836,21024,19490,20433,22598,25107,33442,36836,40548,42927,43462]
#公路货运量(单位：万吨)
freighttraffic=[1237,1379,1385,1399,1663,1714,1834,4322,8132,8936,11099,11203,10524,11115,13320,16762,18673,20724,20803,21804]
# 构建数据字典
data_dict={'population':population,'vehicle':vehicle,'roadarea':roadarea,'passengertraffic':passengertraffic,'freighttraffic':freighttraffic}
# 把数据字典传入dataFrame中
df=pd.DataFrame(data_dict)
#print(df)
# dataFrame存储到csv中
df.to_csv('np_data.csv')

import numpy as np
import pandas as pd
# 题目：根据人数，机动车数，公路面积，预测公路客运量和货运量
# 1.数据读入，然后提取x和y
# （1）读取csv文件
df=pd.read_csv('np_data.csv')
x_df=df.loc[:,'population':'roadarea']
# population（人数）,vehicle（机动车数）,roadarea（公路面积）
y_df=df.loc[:,'passengertraffic':'freighttraffic']
# passengertraffic（公路客运量）,freighttraffic（公路货运量）
# print(x_df)
# print(y_df)
# 如何把dataframe转换为numpy的array
samplein=np.array(x_df)
#print(samplein)
sampleout=np.array(y_df)# [20,2]
# 2.数据标准化（最大最小值标准化） 特征工程
# Max_min 标准化
def max_min_normalization(data):
    # (x-x_min)/(x_max-x_min)
    # (1)提取数据的最大值和最小值
    data_max=data.max(axis=0)
    data_min=data.min(axis=0)
    # (2)实现数据的max_min标准化
    new_data=(data-data_min)/(data_max-data_min)
    return data_max,data_min,new_data
'''
[[20.55  0.6   0.09]
 [22.44  0.75  0.11]
 [25.37  0.85  0.11]
 [27.13  0.9   0.14]
 [29.45  1.05  0.2 ]
 [30.1   1.35  0.23]
 [30.96  1.45  0.23]
 [34.06  1.6   0.32]
 [36.42  1.7   0.32]
 [38.09  1.85  0.34]
 [39.13  2.15  0.36]
 [39.99  2.2   0.36]
 [41.93  2.25  0.38]
 [44.59  2.35  0.49]
 [47.3   2.5   0.56]
 [52.89  2.6   0.59]
 [55.73  2.7   0.59]
 [56.76  2.85  0.67]
 [59.17  2.95  0.69]
 [60.63  3.1   0.79]]
'''
samplein_max,samplein_min,samplein_norm=max_min_normalization(samplein)
samplein_norm=samplein_norm.reshape([3,20])
# samplein_norm shape [20,3]
sampleout_max,sampleout_min,sampleout_norm=max_min_normalization(sampleout)
sampleout_norm=sampleout_norm.reshape([2,20])
# sampleout_norm shape [20,2]
# 增加一点难度，加点噪音数据
noise=0.03*np.random.rand(samplein_norm.shape[0],samplein_norm.shape[1])
samplein_norm+=noise
# 3.构建网络
# (1)超参数
# 迭代次数
epochs=60000
# 学习率
learning_rate=0.025
# 批量数据
batch_size=20
# 输入层维度
indim=3
# 输出层维度
outdim=2
# 隐藏层的神经元个数
hiddendim=8 # 小技巧：一般一开始设置为2的次方的值，之后做参数优化上下调整
#（2）网络设计
# 输入层到隐层的权重和偏置量
w1=0.5*np.random.rand(hiddendim,indim)-0.1
# w1*x=[8,20]=>hidden_out
b1=0.5*np.random.rand(hiddendim,1)-0.1
#
# 隐层到输出层的权重和偏置量
w2=0.5*np.random.rand(outdim,hiddendim)-0.1
# w2*hidden_out=>[2,20]
b2=0.5*np.random.rand(outdim,1)-0.1
# 结构
# 输入层->隐层->输出层
def sigmod(x):
    return 1/(1+np.exp(-x))
# fp
def bp_net_forward(x_input):
    # 隐层的输出
    # hidden_out [8,20]
    hidden_out=sigmod(np.dot(w1,x_input).T+b1.T).T

    # 输出层
    # network_out [2,20]
    network_out=(np.dot(w2,hidden_out).T+b2.T).T
    return network_out,hidden_out
# bp
def bp_net_backward(err,hidden_out):
    global w2
    global w1
    global b1
    global b2
    # 隐层到输出层损失
    delta2=err#输出层损失-》目的是求隐层到输出层权重的变化量
    # w2 [2,8]->T->[8,2] ,delta2 [2,20]
    # [8,20]*[8,20]*(1-[8,20]]
    # np.dot(w2.T,delta2) 输出相当于是每一个数组元素对应的损失值
    # 输入层到隐层损失（-(target-y_out)*out*(1-out)*w2）
    delat1=np.dot(w2.T,delta2)*hidden_out*(1-hidden_out)# 隐层的损失
    #-》目的是求输入层到隐层权重的变化量
    # delta2 [2,20]  hidden_out [8,20]->T->[20,8]
    dw2=np.dot(delta2,hidden_out.T)
    # [2,20] [20,1] -> b[2,1]
    db2=np.dot(delta2,np.ones((batch_size,1)))

    # 输入层到隐层
    dw1=np.dot(delat1,samplein_norm.T)
    # delta1 [8,20] * [20,1] -> b1  [8,1]
    db1=np.dot(delat1,np.ones((batch_size,1)))

    # 权重更新
    w2+=learning_rate*dw2
    b2+=learning_rate*db2
    w1+=learning_rate*dw1
    b1+=learning_rate*db1

# 4.进行训练
loss_list=[]
while True:
    networkout,hidden_out=bp_net_forward(samplein_norm)
    # 损失
    err=sampleout_norm-networkout#shape [2,20]
    sse=sum(sum(err**2))
    loss_list.append(sse)
    print(sse)
    if sse<0.05:
        break
    # bp
    bp_net_backward(err,hidden_out)
    # print('w2',w2)
# 误差曲线图
# pip install pyecharts
# pip install pyecharts_snapshot
from pyecharts import Line,Page
page=Page()
loss_line=Line('loss折线图')
x = [i for i in range(len(loss_list)//100+1)]
y = loss_list[::100]
print(len(x))
print(len(y))
loss_line.add('',x,y)
page.add(loss_line)

# 5.进行预测，查看效果
# 还原标准化
def decode_max_min_norm(data,data_max,data_min):
    # 标准化  (x-x_min)/(x_max-x_min)=data
    # data*（x_max-x_min）+x_min
    diff=data_max-data_min
    x=data*diff.reshape(-1,1)+data_min.reshape(-1,1)
    # x=data
    # x[0]=data[0]*diff[0]+data_min[0]
    # x[1]=data[1]*diff[0]+data_min[0]
    return x

# 一个网页上显示两个图表

# 显示预测客运量，显示真实值和预测值的折线图
networkout,_=bp_net_forward(samplein_norm)
# 还原数据
networkout2=decode_max_min_norm(networkout,sampleout_max,sampleout_min)
sampleout=decode_max_min_norm(sampleout_norm,sampleout_max,sampleout_min)
list1=[i for i in range(20)]
line=Line('客运量预测和真实折线图')
line.add('预测值',list1,networkout2[0]) # [2,20] ->[1,20]
line.add('真实值',list1,sampleout[0])# sampleout [20,2]->T [2,20] -> [20]
page.add(line)

# 显示预测货运量，显示真实值和预测值的折线图
line2=Line('货运量预测和真实折线图')
line2.add('预测值',list1,networkout2[1]) # [2,20] ->[1,20]
line2.add('真实值',list1,sampleout[1])# sampleout [20,2]->T [2,20] -> [20]
page.add(line2)
page.render()


# 代码流程
# 1.数据读入
# 2.特征工程+数据增强+数据预处理
# 3.模型构建
# 4.模型训练+模型持久化 sklearn-》fit_tr () ，tensorflow -》run
# ** 5.模型调参（自动调参《-强化学习）
# 6.模型加载+预测

import numpy as np
import pandas as pd
import tensorflow as tf
# # pip install pyecharts
# # pip install pyecharts_snapshot
from pyecharts import Line, Page
# 题目：根据人数，机动车数，公路面积，预测公路客运量和货运量
# 1.数据读入，然后提取x和y
# （1）读取csv文件
df=pd.read_csv('np_data.csv')
x_df=df.loc[:,'population':'roadarea']
# population（人数）,vehicle（机动车数）,roadarea（公路面积）
y_df=df.loc[:,'passengertraffic':'freighttraffic']
# passengertraffic（公路客运量）,freighttraffic（公路货运量）
# print(x_df)
# print(y_df)
# 如何把dataframe转换为numpy的array
samplein=np.array(x_df,dtype=np.float32)# [20,3]
#print(samplein)
sampleout=np.array(y_df,dtype=np.float32)# [20,2]
def max_min_normalization(data):
    # (x-x_min)/(x_max-x_min)
    # (1)提取数据的最大值和最小值
    data_max=data.max(axis=0)
    data_min=data.min(axis=0)
    # (2)实现数据的max_min标准化
    new_data=(data-data_min)/(data_max-data_min)
    return data_max,data_min,new_data
'''
[[20.55  0.6   0.09]
 [22.44  0.75  0.11]
 [25.37  0.85  0.11]
 [27.13  0.9   0.14]
 [29.45  1.05  0.2 ]
 [30.1   1.35  0.23]
 [30.96  1.45  0.23]
 [34.06  1.6   0.32]
 [36.42  1.7   0.32]
 [38.09  1.85  0.34]
 [39.13  2.15  0.36]
 [39.99  2.2   0.36]
 [41.93  2.25  0.38]
 [44.59  2.35  0.49]
 [47.3   2.5   0.56]
 [52.89  2.6   0.59]
 [55.73  2.7   0.59]
 [56.76  2.85  0.67]
 [59.17  2.95  0.69]
 [60.63  3.1   0.79]]
'''
samplein_max,samplein_min,samplein_norm=max_min_normalization(samplein)
# samplein_norm shape [20,3]
sampleout_max,sampleout_min,sampleout_norm=max_min_normalization(sampleout)
# sampleout_norm shape [20,2]
# 增加一点难度，加点噪音数据
noise=0.03*np.random.rand(sampleout.shape[0],sampleout.shape[1])
sampleout+=noise
# 2.构建网络
# (1)超参数
# 迭代次数
epochs=60000
# 学习率
learning_rate=0.025
# 批量数据
batch_size=20
# 输入层维度
indim=3
# 输出层维度
outdim=2
# 隐藏层的神经元个数
hiddendim=8 # 小技巧：一般一开始设置为2的次方的值，之后做参数优化上下调整
# 结构
# 输入层->隐层->输出层
x_input=tf.placeholder(dtype=tf.float32,shape=[None,3])
y_out=tf.placeholder(dtype=tf.float32,shape=[None,2])
# fp
def network(input_x):
    # 输入层到隐层
    with tf.name_scope('input_hidden'):
        # w1 [3,8]  x [20,3]
        w1 = tf.get_variable('w1', shape=[indim, hiddendim])
        # x*w1=[20,8]=>hidden_out
        b1=tf.get_variable('b1',shape=[hiddendim])
        hidden_out=tf.nn.sigmoid(tf.add(tf.matmul(input_x,w1),b1))
    # 隐层到输出层
    with tf.name_scope('hidden_out'):
        # 隐层到输出层的权重和偏置量
        w2 = tf.get_variable('w2', shape=[hiddendim, outdim])
        # w2*hidden_out=>[2,20]
        b2 = tf.get_variable('b2', shape=[outdim])
        network_out=tf.add(tf.matmul(hidden_out,w2),b2)
    return network_out

# 一般这种预测操作，使用方式为 取数据预测，1个结果


#acc=tf.reduce_mean(tf.cast(tf.equal(networkout,y_out),tf.float32))
# 4.进行训练
def train():
    networkout = network(x_input)
    cost = tf.reduce_mean(0.5 * tf.reduce_sum((y_out - networkout) ** 2))
    op = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)
    with tf.Session() as sess:
        sess.run(tf.global_variables_initializer())
        saver=tf.train.Saver()
        loss_list=[]
        for i in range(epochs):
            _,loss=sess.run([op,cost],feed_dict={x_input:samplein_norm,y_out:sampleout_norm})
            loss_list.append(loss)
        saver.save(sess,'model/bp')
    # 误差曲线图
    loss_line=Line('loss折线图')
    loss_line.add('',[i for i in range(100)],loss_list[:100])
    loss_line.render('loss_render.html')

def predict():
    networkout = network(x_input)
    sess=tf.Session()
    saver = tf.train.Saver()
    saver.restore(sess,'model/bp')
    pre=sess.run(networkout,feed_dict={x_input:samplein_norm})
    sess.close()
    # pre [20,2]


    page=Page()
    # loss_line=Line('loss折线图')
    # loss_line.add('',[i for i in range(len(loss_list)//100)],loss_list[::100])
    # page.add(loss_line)
    #
    # # 5.进行预测，查看效果
    # # 还原标准化
    def decode_max_min_norm(data,data_max,data_min):
        # 标准化  (x-x_min)/(x_max-x_min)=data
        # data*（x_max-x_min）+x_min
        diff=data_max-data_min
        x=data*diff+data_min
        # x=data
        # x[0]=data[0]*diff[0]+data_min[0]
        # x[1]=data[1]*diff[0]+data_min[0]
        return x
    #
    # # 一个网页上显示两个图表
    #
    # 显示预测客运量，显示真实值和预测值的折线图
    # 还原数据
    networkout2=decode_max_min_norm(pre,sampleout_max,sampleout_min)
    sampleout=decode_max_min_norm(sampleout_norm,sampleout_max,sampleout_min)
    list1=[i for i in range(20)]
    line=Line('客运量预测和真实折线图')
    line.add('预测值',list1,networkout2[:,0]) # [2,20] ->[1,20]
    line.add('真实值',list1,sampleout[:,0])# sampleout [20,2]->T [2,20] -> [20]
    page.add(line)
    # 显示预测货运量，显示真实值和预测值的折线图
    line2=Line('货运量预测和真实折线图')
    line2.add('预测值',list1,networkout2[:,1]) # [2,20] ->[1,20]
    line2.add('真实值',list1,sampleout[:,1])# sampleout [20,2]->T [2,20] -> [20]
    page.add(line2)
    page.render('pre_render.html')
#
#
# # 代码流程
# # 1.数据读入
# # 2.特征工程+数据增强+数据预处理
# # 3.模型构建
# # 4.模型训练+模型持久化 sklearn-》fit_tr () ，tensorflow -》run
# # ** 5.模型调参（自动调参《-强化学习）
# # 6.模型加载+预测
if __name__=='__main__':
    train()
    #predict()

Python实现RBF神经网络

import numpy as np
from scipy.linalg import norm,pinv
class RBF:
    # 初始化
    def __init__(self,indim,outdim,numCenters):
        # indim 输入数据的特征个数
        # outdim 输出数据的结果个数
        # numCenters 中心点数量
        self.indim=indim
        self.outdim=outdim
        self.numCenters=numCenters
        self.W=np.random.random((self.numCenters,self.outdim))# 中心层到输出层的权重
        self.beta=16
        self.centers=[np.random.uniform(-1,1,indim) for i in range(numCenters)]# 中心点的初始化,可以从样本中随机抽样，或者直接使用随机数生成中心点

    #径向计算的函数，计算中心点和传入数据的函数
    # 内插法的方式，完成计算
    # exp(-beta*norm(c-x_i)**2)
    def _basisfunc(self,c,x_i):
        # 一般会进行数据维度的验证，验证传入数据的特征数符合数据条例
        assert len(x_i)==self.indim
        return np.exp(-self.beta*norm(c-x_i)**2)

    # 循环遍历每一个样本和每一个中心点，并且记录P个函数的结果
    def _calcAct(self, X):
        # X 输入数据
        # 1.生成一个空数组，为了记录中心层计算结果
        G = np.zeros((X.shape[0], self.numCenters), np.float32)
        for ci, c in enumerate(self.centers):
            for xi,x in enumerate(X):
                #print(c,'-',x)
                G[xi,ci]=self._basisfunc(c,x)
        return G

    # 传入数据进行训练
    def train(self,X,Y):
        # 打乱数据进行随机抽样，得到中心点
        # 1.随机打乱数据，去除前P个点，作为中心点，执行内插法
        rnd_index=np.random.permutation(X.shape[0])[:self.numCenters]
        # 2.从X数据中随机去除numCenter个索引，对应的数据
        self.centers=[X[i,:] for i in rnd_index]
        G=self._calcAct(X)
        print(G.shape)
        print('*'*10)
        print(np.array(pinv(G)).shape)
        # y=w*x
        # pinv 伪逆矩阵,类似做了一个bp正向和反向
        # 根据x和y反过来计算w的权重
        print(Y.shape)
        self.W=np.dot(pinv(G),Y)
        print(self.W.shape)

    # 预测
    def test(self,X):
        G=self._calcAct(X)
        Y=np.dot(G,self.W)
        return Y

n=2000
#np.mgrid[start:end:step,start2:end2:step2]
# 根据起始start到终止end，以及步长，生成一个二维坐标数组，第一部分是y的坐标，第二部分是是x的坐标
#np.mgrid[start:end:step] 根据起始start到终止end，以及步长，生成一个一维数组
# np.complex创建一个值为real+imag*j 复数
from matplotlib import pyplot as plt
x=np.mgrid[-1:1:np.complex(0,n)].reshape(n,-1)
# print(x)
y=np.cos(3*(x+0.5)**3-1)
# plt.scatter(x,y)
# plt.show()
# 实例化RBF，进行train
rbf=RBF(1,1,20)
rbf.train(x,y)
z=rbf.test(x)
#
plt.scatter(x,y)
plt.plot(x,z,'k-')
plt.show()

SimpleNeuralNetwork简单神经网络实现手写数字案例（TensorFlow实现）

import tensorflow_datasets as tfds
import tensorflow as tf
import os
import pandas as pd
import numpy as np
from sklearn.preprocessing import OneHotEncoder

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
# 1.数据读入
#方法1
mnist = tfds.load('mnist')
mnist_train,mnist_test = mnist['train'],mnist['test']

# mnist_train = tfds.load(name="mnist", split="train")
# mnist_test = tfds.load(name="mnist", split="test")


#方法2
# mnist_builder = tfds.builder("mnist")
# mnist_builder.download_and_prepare()
# mnist_train = mnist_builder.as_dataset(split="train")

# 数据之后使用batch方式直接读取，这里就不要取数据
# 2.特征工程+数据增强+数据预处理（mnist不需要做这一步）
# 3.模型构建
# （1）超参数
batch_size=50# 批数据
epochs=10000 # 迭代次数
lr=1e-5 # 学习率
input_dim=784 # 输入层神经元个数
hidden_layer1_dim=64
hidden_layer2_dim=32
out_dim=10
display_step=100
# （2）神经网络
# a.占位符
x=tf.compat.v1.placeholder(tf.float32,[None,input_dim])
y=tf.compat.v1.placeholder(tf.float32,[None,out_dim])
# dropout  神经元随机屏蔽，类似于决策树中剪枝操作
# drop_out=tf.placeholder(tf.float32)# 0.5,表示当前层50%的神经元输出置零

# b.封装常用操作
# 获取权重
def get_weight(shape):
    return tf.Variable(tf.random.normal(shape))

# 获取偏置量
def get_biases(shape):
    return tf.Variable(tf.random.normal(shape))

# 网络
def BpNetwork(x):
    # 第一层结构
    # x:[None,784]
    hidden_out1=tf.nn.sigmoid(tf.add(tf.matmul(x,get_weight([input_dim,hidden_layer1_dim])),get_biases([hidden_layer1_dim])))
    # 第二层结构
    # hidden_out1 :[None,64]
    hidden_out2=tf.nn.sigmoid(tf.add(tf.matmul(hidden_out1,get_weight([hidden_layer1_dim,hidden_layer2_dim])),get_biases([hidden_layer2_dim])))
    # 输出层
    return tf.add(tf.matmul(hidden_out2,get_weight([hidden_layer2_dim,out_dim])),get_biases([out_dim]))

# （3）loss+ac+opt
pred=BpNetwork(x)
# 损失函数
cost=tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits_v2(logits=pred,labels=y))
# 优化器
optm=tf.compat.v1.train.AdamOptimizer(learning_rate=lr).minimize(cost)
# 准确率
corr=tf.equal(tf.argmax(pred,1),tf.argmax(y,1))
accr=tf.reduce_mean(tf.cast(corr,tf.float32))

mnist_train = mnist_train.repeat().batch(batch_size,drop_remainder=True)
mnist_test = mnist_test.repeat().batch(batch_size,drop_remainder=True)

# prefetch 将使输入流水线可以在模型训练时异步获取批处理。
mnist_train = mnist_train.prefetch(tf.data.experimental.AUTOTUNE)
mnist_test = mnist_test.prefetch(tf.data.experimental.AUTOTUNE)

train_iterator = tf.compat.v1.data.make_one_shot_iterator(mnist_train).get_next()
test_iterator = tf.compat.v1.data.make_one_shot_iterator(mnist_test).get_next()

oneh = OneHotEncoder()
oneh.fit_transform(np.array([i for i in range(10)]).reshape(-1,1))

# 4.模型训练+模型持久化
with tf.compat.v1.Session() as sess:
    # (1)变量初始化
    sess.run(tf.compat.v1.global_variables_initializer())
    saver=tf.compat.v1.train.Saver()# 模型持久化
    # (2) run->optm
    i = 0
    # for i in range(epochs):
    while True:
        train_datas = sess.run(train_iterator)
        batch_xs = train_datas['image'].reshape(batch_size,-1)
        batch_ys = oneh.transform(train_datas['label'].reshape(-1,1)).todense() #todense()把稀疏矩阵转化为稠密矩阵

        feeds={x:batch_xs,y:batch_ys}
        sess.run(optm,feed_dict=feeds)
        if (i)%display_step==0:
            train_feeds = {x: batch_xs, y: batch_ys}

            test_datas = sess.run(train_iterator)
            batch_test_xs = train_datas['image'].reshape(batch_size,-1)
            batch_test_ys = oneh.transform(test_datas['label'].reshape(-1, 1)).todense()

            test_feeds = {x: batch_test_xs, y: batch_test_ys}
            # 查看训练准确率和测试准确率
            train_acc=sess.run(accr,feed_dict=train_feeds)
            test_acc=sess.run(accr,feed_dict=test_feeds)
            print('step:{},train-acc:{},test-acc:{}'.format(i,train_acc,test_acc))
            if train_acc>0.9 and test_acc>0.9:
                # 持久化
                saver.save(sess,'model/mnist.ckpt',global_step=i)
                break
        i+=1

# ** 5.模型调参（自动调参《-强化学习）
# 6.模型加载+预测（暂不做）