拉格朗日插值法理论与编程实现

插值法

什么是插值

插值是一种古老的数学方法，早在1000多年前我国学者在研究历法时就应用了线性插值和抛物插值，到了17—19世纪，为了解决航海和天文观测中的一些实际问题，Newton，Lagrange，和Hermite等数学家较系统的研究了插值法。

简单的说，插值就是通过离散的数据点，去求一条经过所有数据点的多项式函数去逼近未知的函数f(x)。

比方说我们收集到了最近一周的气温数据，但是由于某些原因，星期四的数据丢失了

日期	周一	周二	周三	周四	周五	周六	周日
气温	17	20	21	不知道	23	22	19

画在坐标图上

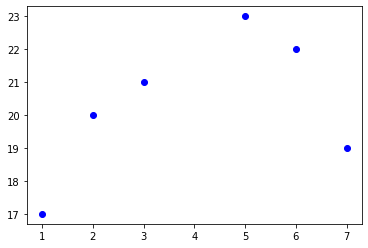
我们很自然的就想到能不能用观察到的六天的气温值，去填补缺失的那一天的气温值

于是我们画出一条曲线经过所有的点(插值条件），那么这条曲线就体现了7天内气温的波动趋势

然后我们从中找出星期四的对应的温度估值，是22.2

日期	周一	周二	周三	周四	周五	周六	周日
气温	17	20	21	22.2	23	22	19

为什么要插值

其实，刚刚的那条曲线，是用原本的6个点的数据构造出来的5次插值多项式曲线

然而事实上，这条多项式曲线是可以通过解方程组求出它的具体表达式的。

我们可以这样来考虑，假设原本的温度分布是服从一个函数f(x)的，但是我们不知道f(x)是什么，于是我们只好通过f(x)的某些具体值（某几天的天气)，去构造一条曲线P(x)来尽可能的拟合f(x)

因为过平面上6个点，最多只能构造出一条5次曲线

于是我们假设要构造的曲线为:

\[P_n(x) = a_0 + a_1x + a_2x^2 + a_3x^3 + a_4x^4 + a_5x^5 \]

我们要求的是系数:

\[a_0,a_1,a_2,a_3,a_4,a_5 \]

因为我们得到了6个数据点，所以我们可以通过求线性方程组来解出待定系数：

\[\begin{cases}a_0 + a_1x_1 + a_2x_1^2 + a_3x_1^3 + a_4x_1^4 + a_5x_1^5 = y_1\\a_0 + a_1x_2 + a_2x_2^2 + a_3x_2^3 + a_4x_2^4 + a_5x_2^5 = y_2\\a_0 + a_1x_3 + a_2x_3^3 + a_3x_3^3 + a_4x_3^4 + a_5x_3^5 = y_3\\a_0 + a_1x_4 + a_2x_4^2 + a_3x_4^3 + a_4x_4^4 + a_5x_4^5 = y_4\\a_0 + a_1x_5 + a_2x_5^2 + a_3x_5^3 + a_4x_5^4 + a_5x_5^5 = y_5\\a_0 + a_1x_6 + a_2x_6^2 + a_3x_6^3 + a_4x_6^4 + a_5x_6^5 = y_6\\\end{cases} \]

写成矩阵方程的形式：

\[\begin{bmatrix}1 & x_1 & x_1^2 & x_3^3 & x_4^4 & x_5^5\\1 & x_2 & x_2^2 & x_2^3 & x_2^4 & x_2^5\\1 & x_3 & x_3^2 & x_3^3 & x_3^4 & x_3^5\\1 & x_4 & x_4^2 & x_4^3 & x_4^4 & x_4^5\\1 & x_5 & x_5^2 & x_5^3 & x_5^4 & x_5^5\\1 & x_6 & x_6^2 & x_6^3 & x_6^4 & x_6^5\\\end{bmatrix}\begin{bmatrix}a_0 \\ a_1 \\ a_2 \\ a_3 \\ a_4 \\ a_5 \\\end{bmatrix}=\begin{bmatrix}y_1 \\ y_2 \\ y_3 \\ y_4 \\ y_5 \\ y_6 \\\end{bmatrix} \]

可以看到左边是一个范德蒙矩阵V，并且我们知道若\(x_i\)各不相同（也即是各行线性无关），则

\[det(V)\neq0 \]

根据线性代数的知识，方程组有且仅有唯一解(或者说，这个方程组有5个未知数，5个不相同的方程，是可以解出唯一解的），是可以直接求逆或者用其他方法求出它的系数来的，但是这样求解计算量特别大，而且范德蒙矩阵很可能是一个病态矩阵，所以不好求。

但是我们可以根据这个函数的一些性质，比如说零点的性质去构造出满足条件的曲线。

拉格朗日插值法

核心思想

核心思想其实很简单，因为我们想要让曲线经过所有的观测点，也即是求一个P(x)，使得

\(P(x_1)=y_1, P(x_2)=y_2, P(x_i)=y_i\)，于是构造出这样的一种形式

\[P(x) = y_1 L_1(x) + y_2 L_2(x) + \dots y_i L_i(x) \]

使得它满足上面的要求，比方说

当\(x=x_1\)时， 要让\(P(x_1) = y_1L_1(x_1) + y_2L_2(x_1)+\dots y_iL_i(x_i) = y1\)​

很容易想到，如果能让\(L_1(x_1) = 1\)，而其他的\(L_i(x_1)=0 (i \neq 1)\)，就可以满足要求了

所以问题转变为怎么求这一组\(L_i(x)\)，使得

\[\begin{cases}L_i(x_i) = 1\\L_i(x_j) = 0 (j \neq i)\end{cases} \]

下面我们从最简单的线性形式开始讨论起

1.线性插值

线性插值是针对两个点的情形的，比如这样

有这样的两个点\(p_0(1,5),p_1(3,7)\)

两点决定一点直线，根据初高中的知识，我们可以用两点式来求出这条直线，如下

\[y = \frac{(y_1-y_0)}{x_1-x_0}(x-x_0) + y_0 \]

然后我们想，这条式子都用到了\(y_1\)和\(y_0\)，根据刚刚的讨论，我们能不能凑出刚刚的那种形式呢?

然后，一波骚操作如下:

\[\begin{align}y &= \frac{y_1 - y_0}{x_1 - x_0}(x-x_0) + y_0\\ &= y_1\frac{x-x_0}{x_1-x_0} + y_0\frac{x-x_0}{x_0-x_1} + y_0\\ &= y_0\frac{x-x_1}{x_0-x_1} + y_1\frac{x-x_0}{x_1-x_0}\end{align} \]

粗乃了！

\[P(x) = y_0\frac{x-x_1}{x_0-x_1} + y_1\frac{x-x_0}{x_1-x_0} \]

所以

\[L_0(x) = \frac{x-x_1}{x_0-x_1}\\L_1(x) = \frac{x-x_0}{x_1-x_0} \]

正好满足要求\(L_0(x_0)=1,L_0(x_1)=0\)

2.抛物插值

上面的线性的还很简单，如果是抛物插值呢（二次函数）

比如说有三个点，\(p_0(1,2), p_1(2,6), P_2(5,8)\)， 得出二次插值多项式如图

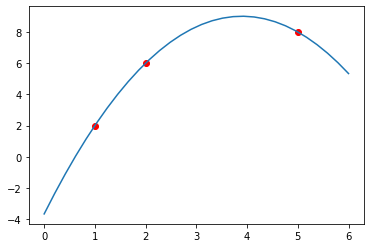
怎么求呢？

\[P(x) = y_0L_0(x) + y_1L_1(x) + y_2L_2(x) \]

观察刚刚的线性的情况，\(L_0(x)= \frac{x-x_1}{x_0-x_1}\)，是一个分式！

分式有什么特点呢？（假设分母不为0）

• 当分子为0，不论分母取什么，整个分式都为0

• 当分子不为0，如果分子和分母相等，则分式等于1

来了！

我们要让\(L_i(x_j)=0,(j \neq i)\)，所以只要让分子等于0即可，然而这样的j可能不止一个，如果有多个怎么办？

我们又想到，0乘以任何数都为0，所以我们可以构造成因式相乘的形式！

所以对于\(L_0(x)=\frac{a}{b}\)，我们可以让他的分子\(a = (x-x_1)(x-x_2)\)，那就满足了

还有呢？

我们要让\(L_i(x_i) = 1\)，在这里，也即是\(L_0(x_0)=1\)，这时它的分子\(a=(x_0-x_1)(x_0-x_2)\)，那还不简单！让它的分母等于这个时候的分子不就行了嘛！

所以...

对于\(L_0(x)\)，\(b = (x_0-x_1)(x_0-x_2)\),也即是\(L_0(x) = \frac{(x-x_1)(x-x_2)}{x_0-x_1(x_0-x_2)}\)

其他也一样

\[L_0(x) = \frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}\\L_1(x) = \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)}\\L_2(x) = \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} \]

粗乃了！

\[P(x) = y_0 \frac{(x-x_1)(x-x_2)}{(x_0-x_1(x_0-x_2)}+y_1 \frac{(x-x_0)(x-x_2)}{(x_1-x_0)(x_1-x_2)} +y_2 \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} \]

3.多项式插值（一般情形）

有了上面的基础，我们很容易就可以把这种思想推广到多项式的形式

回到最初的起点，我们有6个观测值，我们可以构造一个5次多项式

它长这样，

\[P(x) = y_0L_0(x) + y_1L_1(x) + y_2L_2(x) + y_3L_3(x) + y_4L_4(x) + y_5L_5(x) \]

仿造上面的构造方法，我们很容易得出

\[L_0(x) = \frac{(x-x_1)(x-x_2)(x-x_3)(x-x_4)(x-x_5)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)(x_0-x_4)(x_0-x_5)}\\L_1(x) = \frac{(x-x_0)(x-x_2)(x-x_3)(x-x_4)(x-x_5)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)(x_1-x_4)(x_1-x_5)}\\L_2(x) = \frac{(x-x_0)(x-x_1)(x-x_3)(x-x_4)(x-x_5)}{(x_2-x_0)(x_2-x_1)(x_2-x_3)(x_2-x_4)(x_2-x_5)}\\L_3(x) = \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_4)(x-x_5)}{(x_3-x_0)(x_3-x_1)(x_3-x_2)(x_3-x_4)(x_3-x_5)}\\L_4(x) = \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_3)(x-x_5)}{(x_4-x_0)(x_4-x_1)(x_4-x_2)(x_4-x_3)(x_4-x_5)}\\L_5(x) = \frac{(x-x_0)(x-x_1)(x-x_2)(x-x_3)(x-x_4)}{(x_5-x_0)(x_5-x_1)(x_5-x_2)(x_5-x_3)(x_5-x_4)}\\ \]

于是我们很快就能得到一般规律,

若有n+1个插值点，要构造n次Lagrange插值公式，则 (\(\prod\)是累乘的意思)

\[L_i(x) = \prod_{j=0,j\neq k}^{n} \frac{x-x_j}{x_i - x_j}\\P_n(x) = \sum_{i=0}^{n}y_iL_i(x) \]

事实上，\(L_i(x)\)被称作插值基函数(n次插值，基函数就是n次多项式的因式分解形式），就像是线性代数里的基一样，我们求得了一组基，就可以通过基的组合求出n次Lagrange插值函数，组合系数（坐标）恰好就是对应插值结点上的函数值\(y_i\)

4.编程实现

有了理论支撑，我们就可编程去实现这个算法了！

而且这个算法的实现非常的计算机友好，只需要两个for循环即可

这里直接给出代码：(Python实现)

import numpy as np
from matplotlib import pyplot as plt


''' 关键代码 '''
def Lagrange(X,Y,x):   #X是观测点的横坐标数组，Y是纵坐标数组,x是要求的点的横坐标（可以是数组）
    n = len(X)          #n个观测点，对应n-1次插值
    y = 0               #y的初值设为0
    for i in range(n):
        L = 1           #把插值基函数初始化为1
        for j in range(n):
            if(i!=j):
                L*=(x-X[j])/(X[i]-X[j]) #按照刚刚的公式算出个分式然后累乘
        y+=Y[i]*t    #然后是累加
    return y




'''调用一下看看'''
X = np.array([1,2,3,5,6,7])
Y = np.array([17,20,21,23,22,19])
x = np.linspace(1,7,50)  #生成区间1到7等距的50个值
y = Lagrange(X,Y,x)     #求出对于的50个插值
plt.plot(X,Y,'ob',x4,y4,'or',x,y)  #画图

牛顿插值法（太懒了，先歇会儿）