最小二乘法

最小二乘法原理与编程实现

背景

数据与数据（变量与变量）之间，很多时候是存在一些关系的，如线性关系和非线性关系。我们常常会希望找到数据之间的关系，用一个函数（或者一条曲线）去描述两个变量之间的关系。
然而因为各种原因，测量得到的数据是会存在误差的，于是我们要一种方法去减少误差带来的干扰，尽可能的描绘出数据之间的关系，这个方法就是最小二乘法，也称最小方差法。

原理

比如说，我们得到了四对数据，分别是（1，0.9），（2, 2.3），（3.5, 2.6），（4, 3.8）把它们画在平面直角坐标系上

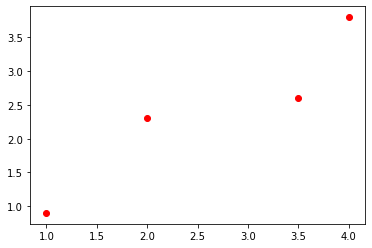
从图像上我们很容易发现，这些点大致分布在一条直线上面，于是我们大胆的猜测y与x呈线性关系，于是我们很自然地想要用一条直线去拟合他们。
也就是

\[y = kx + b \]

然而，事实是它们只是看起来像一条直线，但实际上并不是一条直线。把方程组列出来，

\[\begin{cases} 1k + b = 0.9 \\ 2k + b = 2.3 \\ 3.5k + b = 2.6 \\ 4k + b = 3.8 \\ \end{cases} \]

求解一下就会发现，这个方程组无解！从图像上来看就是我们找不到一条直线通过所有的点。
那该怎么办？那我们只好退一步，不要求找一条完全经过所有点的直线，只要求找一条能够大致刻画它们关系的直线，并且使得误差最小。那误差怎么衡量呢？
我们随便画一条直线，比如说

\[y = kx + b\\(图例k=1,b=0) \]

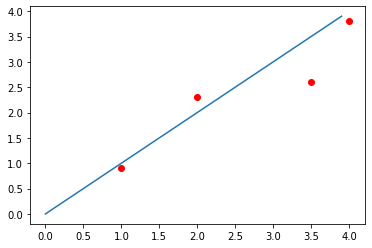
因为有些点没有落到直线上，于是我们把误差定义为每一个观测点的y值和我们预测的真实值之间的距离的平方,也就是

\[e_i = (f(x_i)-y_i)^2=(kx_i + b - y_i)^2 \]

我们的目标是使得总体的误差最小，也就是

\[min(\sum_{i=1}^n{e_i}) \]

这是一条关于k和b的二元函数，我们求偏导数并找到导数为0的点就可以使其最小，也即是令

\[\begin{cases}\frac{\partial{e}}{\partial{k}}=2\sum{(kx_i + b-y_i)x_i} = 0 \\\frac{\partial{e}}{\partial{b}}=2\sum{(kx_i + b-y_i)} = 0 \\\end{cases} \]

我们把原来的方程组写成矩阵的形式(这里把k,b当成待求参数，写成\(x_1,x_2\))

\[\begin{bmatrix} 1 & 1 \\ 2 & 1 \\ 3.5 & 1 \\ 4 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} =\begin{bmatrix} 0.6\\3\\2.6\\3.8 \end{bmatrix}\]

然后我们把误差写成列向量，也就是

\[\begin{bmatrix} e_1\\e_2\\e_3\\e_4 \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 2 & 1 \\ 3.5 & 1 \\ 4 & 1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} -\begin{bmatrix} 0.6\\3\\2.6\\3.8 \end{bmatrix} \]

记

\[E =\begin{bmatrix}e_1\\e_2\\e_3\\e_4\end{bmatrix}, A =\begin{bmatrix}1 & 1 \\2 & 1 \\3.5 & 1 \\4 & 1 \end{bmatrix}, X = \begin{bmatrix}x_1 \\ x_2\end{bmatrix}, b = \begin{bmatrix}0.6\\3\\2.6\\3.8\end{bmatrix} \]

则得到

\[E = AX - b \]

要让\(E^2\)最小，即

\[E^TE = (AX-b)^T(AX-b) \]

我们对X求导

\[\frac{\partial{E^2}}{\partial{X}}= \frac{\partial{(AX-b)^T(AX-b)}}{\partial{X}}\\= \frac{\partial{(AX-b)^T}}{\partial{X}} *(AX-b)+ \frac{\partial{(AX-b)^T}}{\partial{X}}*(AX-b)\\= 2\frac{\partial{(AX-b)^T}}{\partial{X}}*(AX-b)\\ =2\frac{\partial{(AX)}^T}{\partial{X}}*(AX-b)\\ =2A^T(AX-b) \]

我们令其等于0，就可以解出X

\[X = (A^TA)^{-1}A^Tb \]

这是经过计算分析得到的，那有没有一些更加直觉化的解析呢？

有！我们可以通过向量的角度去理解它的原理！

刚刚那个矩阵方程可以写成向量方程的形式，

\[\begin{bmatrix}1 & 1 \\2 & 1 \\3.5 & 1 \\4 & 1 \end{bmatrix}\begin{bmatrix}x_1 \\ x_2\end{bmatrix}=x_1\begin{bmatrix}1 \\2 \\3.5 \\4 \\\end{bmatrix}+x_2\begin{bmatrix}1 \\1 \\1 \\1 \end{bmatrix}=\begin{bmatrix}0.6\\3\\2.6\\3.8\end{bmatrix} \]

我们记

\[v_1 = \begin{bmatrix} 1 \\ 2 \\ 3.5 \\ 4 \\ \end{bmatrix}, v_2 = \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix} b = \begin{bmatrix} 0.6\\3\\2.6\\3.8 \end{bmatrix} \]

容易看到，\(v_1\)和\(v_2\)是线性无关的，也就是它们的线性组合可以张成四维空间里的一个平面。

我们想要找的是它的某种组合使得其等于b，但这种组合找不到，于是我们就去找那个平面里的一条线，使得它到b的距离最短。容易想象那条线就是b在span(\(v_1,v_2\))下的投影，我们记该投影向量为c ，则b和c之间的距离就是\(||b-c||\),我们记为e，这时e最小，且满足e垂直与span(\(v_1,v_2\))。所以e肯定也垂直于\(v_1,v_2\)，即是

\[ev_1=0,ev_2=0\\ev_1+ev_2=0\\\begin{bmatrix}1\\2\\3.5\\4\end{bmatrix}*e+\begin{bmatrix}1\\1\\1\\1\end{bmatrix}*e=0\\ \]

这里是点乘，写成矩阵相乘就是

\[\begin{bmatrix}1&2&3.5&4\\1&1&1&1\end{bmatrix}e=0\\ \]

注意到这里是A的转置\(A^T\),再把e=(AX-b)代入得

\[A^T(AX-b)=0 \]

结果是和上面推导的一样的

以上的方法对于二次，三次拟合都是成立的，具体可以参考其他资料。

拟合的结果

一次拟合

###二次拟合 ###三次拟合 ##代码(Python)

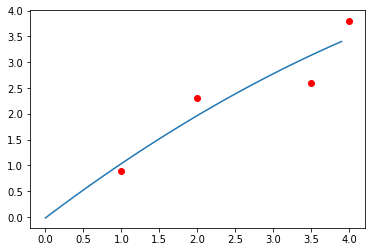
# -*- coding: utf-8 -*-
"""
Created on Mon Feb 17 13:51:43 2020
最小二乘法
@author: urahyou
"""
import numpy as np
import matplotlib.pyplot as plt

x = np.array([3.0, 5, 6, 8, 10])
y = np.array([5.0, 2, 1, 2, 4])

p1 = plt.scatter(x,y,c='red')

def LSD(x, y, n):
    N = x.size  #获取方程组个数
    A = np.ones(N)
    
    for i in range(1, n+1):
        A = np.vstack((A,x**i))  #垂直拼接
    A = A.T  #转置回来
    #求解
    B = np.linalg.inv(A.T@A)@A.T
    #求出解系数
    sol = np.dot(B, y)
    return sol

def poly(x,sol):
    y =  np.zeros_like(x)  #每一个x,对应一个y
    n = sol.size
    for i in range(n):
        y += sol[i]*x**i
    return y


sol = LSD(x,y,2)
X = np.arange(0, 14, 0.1)
Y = poly(X,sol)
p2 = plt.plot(X,Y)